LM$^2$otifs : An Explainable Framework for Machine-Generated Texts Detection

The impressive ability of large language models to generate natural text across various tasks has led to critical challenges in authorship authentication. Although numerous detection methods have been developed to differentiate between machine-generated texts (MGT) and human-generated texts (HGT), the explainability of these methods remains a significant gap. Traditional explainability techniques often fall short in capturing the complex word relationships that distinguish HGT from MGT. To address this limitation, we present LM$^2$otifs, a novel explainable framework for MGT detection. Inspired by probabilistic graphical models, we provide a theoretical rationale for the effectiveness. LM$^2$otifs utilizes eXplainable Graph Neural Networks to achieve both accurate detection and interpretability. The LM$^2$otifs pipeline operates in three key stages: first, it transforms text into graphs based on word co-occurrence to represent lexical dependencies; second, graph neural networks are used for prediction; and third, a post-hoc explainability method extracts interpretable motifs, offering multi-level explanations from individual words to sentence structures. Extensive experiments on multiple benchmark datasets demonstrate the comparable performance of LM$^2$otifs. The empirical evaluation of the extracted explainable motifs confirms their effectiveness in differentiating HGT and MGT. Furthermore, qualitative analysis reveals distinct and visible linguistic fingerprints characteristic of MGT.

Explanation-Preserving Augmentation for Semi-Supervised Graph Representation Learning

Graph representation learning (GRL), enhanced by graph augmentation methods, has emerged as an effective technique achieving performance improvements in wide tasks such as node classification and graph classification. In self-supervised GRL, paired graph augmentations are generated from each graph. Its objective is to infer similar representations for augmentations of the same graph, but maximally distinguishable representations for augmentations of different graphs. Analogous to image and language domains, the desiderata of an ideal augmentation method include both (1) semantics-preservation; and (2) data-perturbation; i.e., an augmented graph should preserve the semantics of its original graph while carrying sufficient variance. However, most existing (un-)/self-supervised GRL methods focus on data perturbation but largely neglect semantics preservation. To address this challenge, in this paper, we propose a novel method, Explanation-Preserving Augmentation (EPA), that leverages graph explanation techniques for generating augmented graphs that can bridge the gap between semantics-preservation and data-perturbation. EPA first uses a small number of labels to train a graph explainer to infer the sub-structures (explanations) that are most relevant to a graph's semantics. These explanations are then used to generate semantics-preserving augmentations for self-supervised GRL, namely EPA-GRL. We demonstrate theoretically, using an analytical example, and through extensive experiments on a variety of benchmark datasets that EPA-GRL outperforms the state-of-the-art (SOTA) GRL methods, which are built upon semantics-agnostic data augmentations.

On Non-Interactive Simulation of Distributed Sources with Finite Alphabets

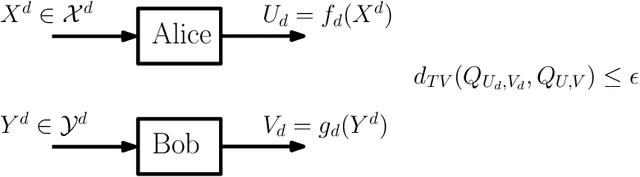
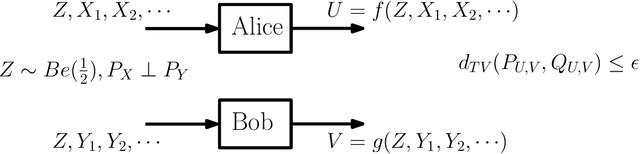
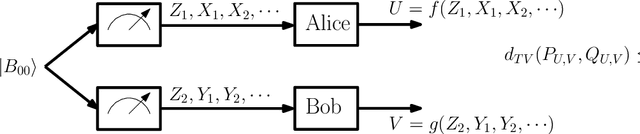
This work presents a Fourier analysis framework for the non-interactive source simulation (NISS) problem. Two distributed agents observe a pair of sequences $X^d$ and $Y^d$ drawn according to a joint distribution $P_{X^dY^d}$. The agents aim to generate outputs $U=f_d(X^d)$ and $V=g_d(Y^d)$ with a joint distribution sufficiently close in total variation to a target distribution $Q_{UV}$. Existing works have shown that the NISS problem with finite-alphabet outputs is decidable. For the binary-output NISS, an upper-bound to the input complexity was derived which is $O(\exp\operatorname{poly}(\frac{1}{\epsilon}))$. In this work, the input complexity and algorithm design are addressed in several classes of NISS scenarios. For binary-output NISS scenarios with doubly-symmetric binary inputs, it is shown that the input complexity is $\Theta(\log{\frac{1}{\epsilon}})$, thus providing a super-exponential improvement in input complexity. An explicit characterization of the simulating pair of functions is provided. For general finite-input scenarios, a constructive algorithm is introduced that explicitly finds the simulating functions $(f_d(X^d),g_d(Y^d))$. The approach relies on a novel Fourier analysis framework. Various numerical simulations of NISS scenarios with IID inputs are provided. Furthermore, to illustrate the general applicability of the Fourier framework, several examples with non-IID inputs, including entanglement-assisted NISS and NISS with Markovian inputs are provided.