Unrolled Primal-Dual Networks for Lensless Cameras

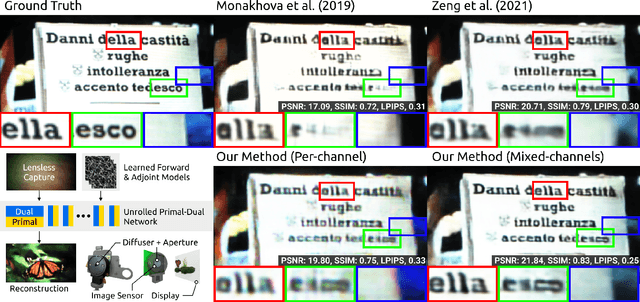
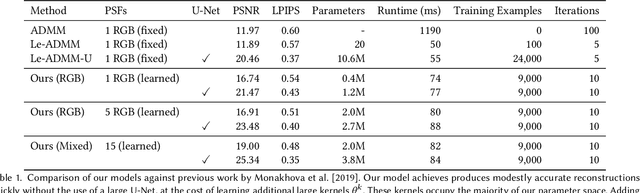
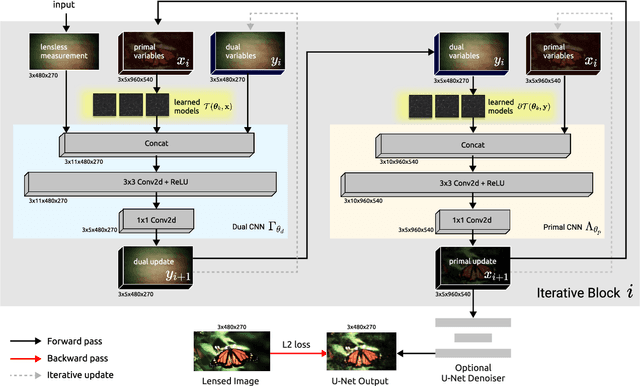
Conventional image reconstruction models for lensless cameras often assume that each measurement results from convolving a given scene with a single experimentally measured point-spread function. These image reconstruction models fall short in simulating lensless cameras truthfully as these models are not sophisticated enough to account for optical aberrations or scenes with depth variations. Our work shows that learning a supervised primal-dual reconstruction method results in image quality matching state of the art in the literature without demanding a large network capacity. This improvement stems from our primary finding that embedding learnable forward and adjoint models in a learned primal-dual optimization framework can even improve the quality of reconstructed images (+5dB PSNR) compared to works that do not correct for the model error. In addition, we built a proof-of-concept lensless camera prototype that uses a pseudo-random phase mask to demonstrate our point. Finally, we share the extensive evaluation of our learned model based on an open dataset and a dataset from our proof-of-concept lensless camera prototype.

Memory-efficient Learning for Large-scale Computational Imaging

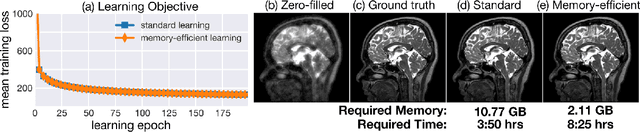
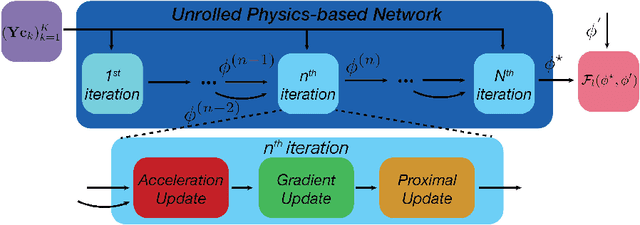
Critical aspects of computational imaging systems, such as experimental design and image priors, can be optimized through deep networks formed by the unrolled iterations of classical model-based reconstructions (termed physics-based networks). However, for real-world large-scale inverse problems, computing gradients via backpropagation is infeasible due to memory limitations of graphics processing units. In this work, we propose a memory-efficient learning procedure that exploits the reversibility of the network's layers to enable data-driven design for large-scale computational imaging systems. We demonstrate our method on a small-scale compressed sensing example, as well as two large-scale real-world systems: multi-channel magnetic resonance imaging and super-resolution optical microscopy.

Video from Stills: Lensless Imaging with Rolling Shutter

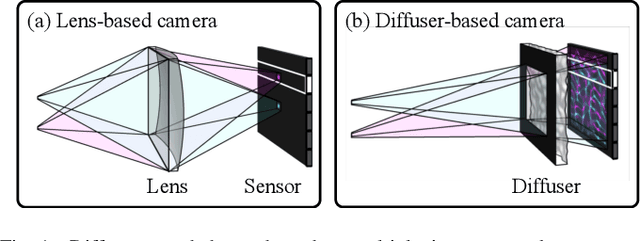
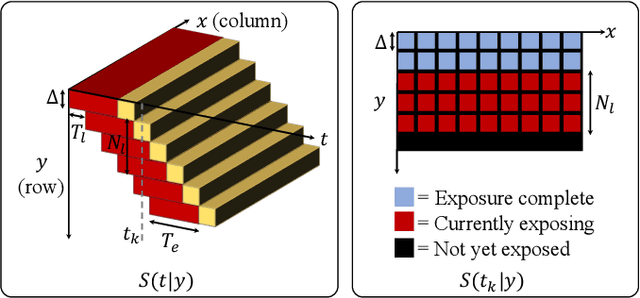
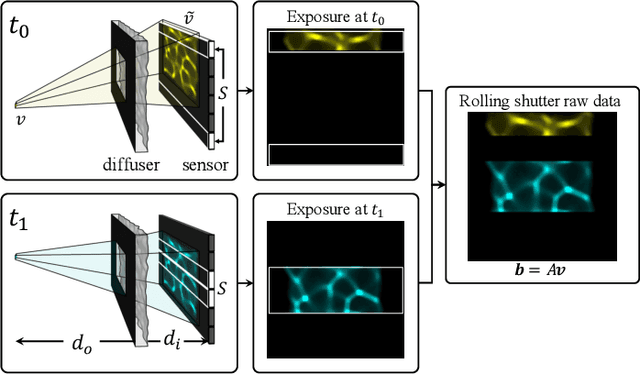
Because image sensor chips have a finite bandwidth with which to read out pixels, recording video typically requires a trade-off between frame rate and pixel count. Compressed sensing techniques can circumvent this trade-off by assuming that the image is compressible. Here, we propose using multiplexing optics to spatially compress the scene, enabling information about the whole scene to be sampled from a row of sensor pixels, which can be read off quickly via a rolling shutter CMOS sensor. Conveniently, such multiplexing can be achieved with a simple lensless, diffuser-based imaging system. Using sparse recovery methods, we are able to recover 140 video frames at over 4,500 frames per second, all from a single captured image with a rolling shutter sensor. Our proof-of-concept system uses easily-fabricated diffusers paired with an off-the-shelf sensor. The resulting prototype enables compressive encoding of high frame rate video into a single rolling shutter exposure, and exceeds the sampling-limited performance of an equivalent global shutter system for sufficiently sparse objects.

Data-Driven Design for Fourier Ptychographic Microscopy

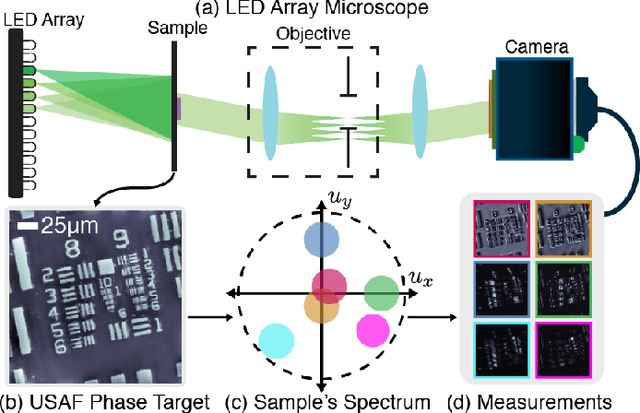
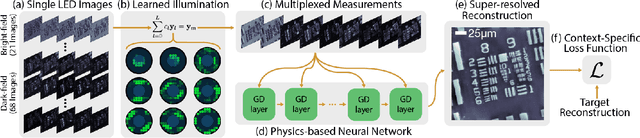
Fourier Ptychographic Microscopy (FPM) is a computational imaging method that is able to super-resolve features beyond the diffraction-limit set by the objective lens of a traditional microscope. This is accomplished by using synthetic aperture and phase retrieval algorithms to combine many measurements captured by an LED array microscope with programmable source patterns. FPM provides simultaneous large field-of-view and high resolution imaging, but at the cost of reduced temporal resolution, thereby limiting live cell applications. In this work, we learn LED source pattern designs that compress the many required measurements into only a few, with negligible loss in reconstruction quality or resolution. This is accomplished by recasting the super-resolution reconstruction as a Physics-based Neural Network and learning the experimental design to optimize the network's overall performance. Specifically, we learn LED patterns for different applications (e.g. amplitude contrast and quantitative phase imaging) and show that the designs we learn through simulation generalize well in the experimental setting. Further, we discuss a context-specific loss function, practical memory limitations, and interpretability of our learned designs.

Physics-based Learned Design: Optimized Coded-Illumination for Quantitative Phase Imaging

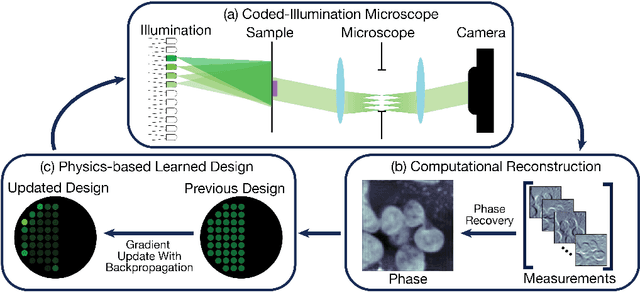
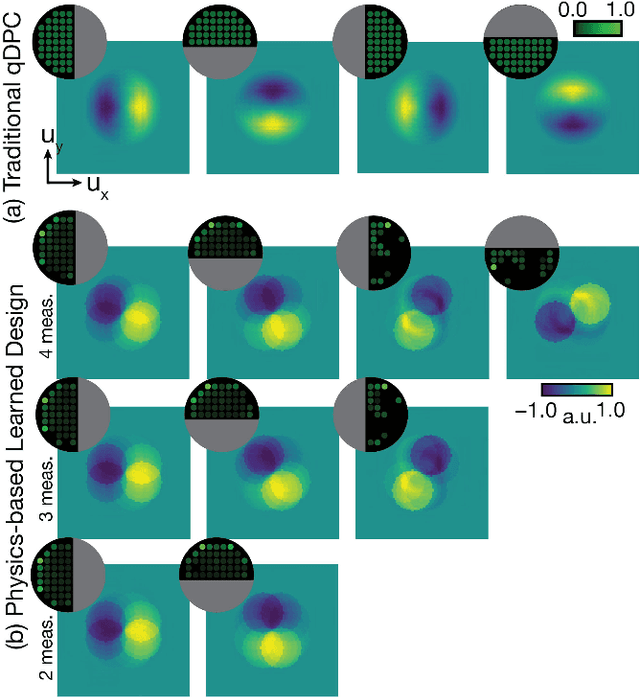
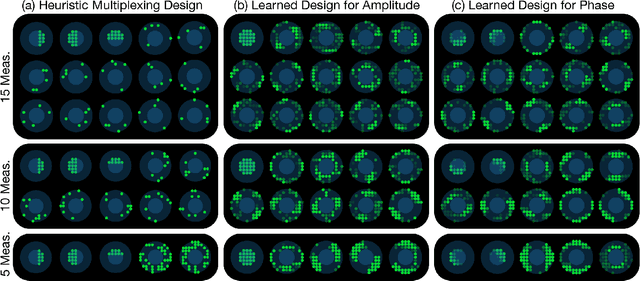
Coded-illumination can enable quantitative phase microscopy of transparent samples with minimal hardware requirements. Intensity images are captured with different source patterns and are processed using non-linear phase retrieval to recover the quantitative phase. The non-linear nature of the processing makes optimizing the coded-illumination pattern designs complicated. Traditional techniques for experimental design (e.g. condition number optimization or spectral analysis) may not be ideal as they characterize linear measurement formation models for linear reconstructions. Deep neural networks (DNNs) offer an end-to-end framework which can efficiently represent the non-linear process and can be optimized over by training. However, DNNs require an enormous amount of training examples and parameters to properly learn the phase retrieval process, without making use of the known physical models. Here, we aim to use both our knowledge of the physics and the power of machine learning together. We develop a new data-driven approach to optimizing coded-illumination patterns for a LED array microscope to maximize performance of a given phase reconstruction algorithm. Our general formulation incorporates the physics of the measurement scheme as well as the non-linearity of the reconstruction algorithm into the design problem. This enables efficient parameterization of the problem, which allows us to use only a small number of training examples to learn designs that generalize well in the experimental setting without retraining. We show experimental results for both a well-characterized phase target and mouse fibroblast cells using coded-illumination patterns optimized for a sparsity-based phase reconstruction algorithm. Our results demonstrate similar accuracy to Fourier Ptychography with 69 measurements, while only using 2 measurements with our learned design.

Learning-based Image Reconstruction via Parallel Proximal Algorithm

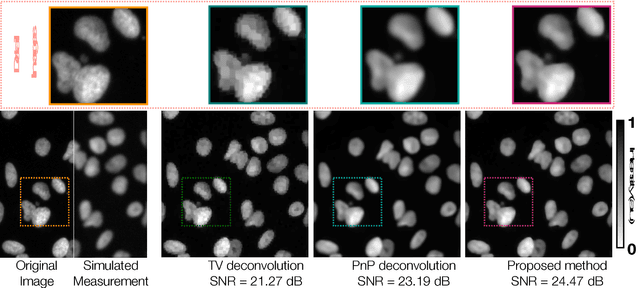
In the past decade, sparsity-driven regularization has led to advancement of image reconstruction algorithms. Traditionally, such regularizers rely on analytical models of sparsity (e.g. total variation (TV)). However, more recent methods are increasingly centered around data-driven arguments inspired by deep learning. In this letter, we propose to generalize TV regularization by replacing the l1-penalty with an alternative prior that is trainable. Specifically, our method learns the prior via extending the recently proposed fast parallel proximal algorithm (FPPA) to incorporate data-adaptive proximal operators. The proposed framework does not require additional inner iterations for evaluating the proximal mappings of the corresponding learned prior. Moreover, our formalism ensures that the training and reconstruction processes share the same algorithmic structure, making the end-to-end implementation intuitive. As an example, we demonstrate our algorithm on the problem of deconvolution in a fluorescence microscope.

DiffuserCam: Lensless Single-exposure 3D Imaging

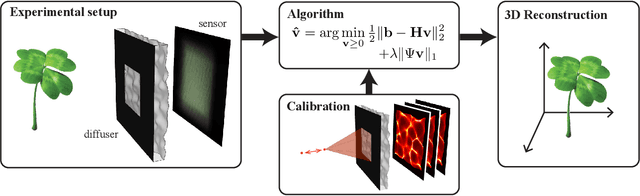
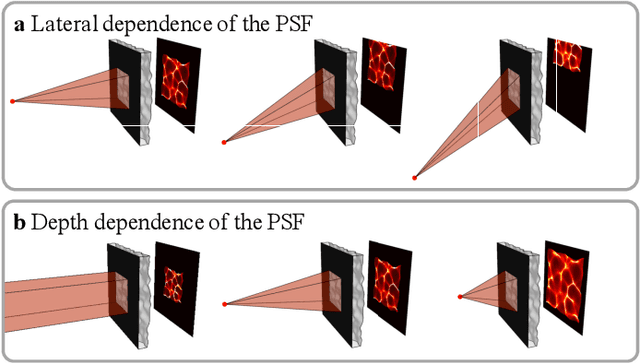
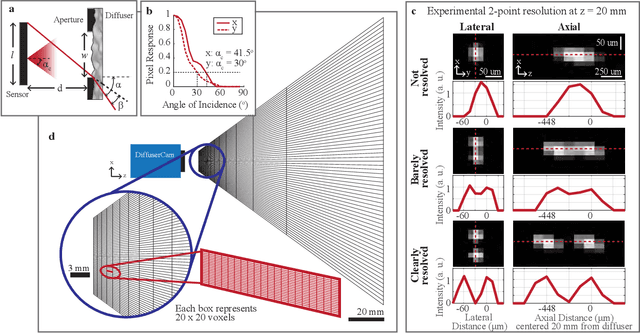
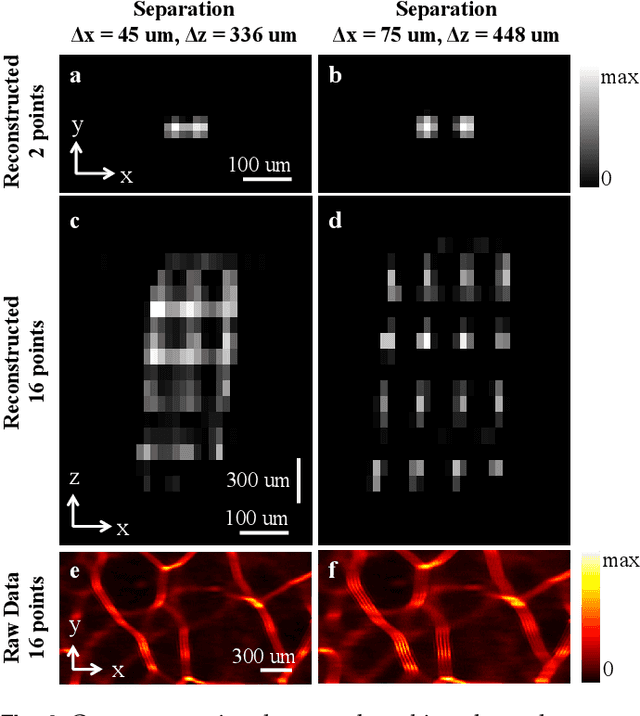
We demonstrate a compact and easy-to-build computational camera for single-shot 3D imaging. Our lensless system consists solely of a diffuser placed in front of a standard image sensor. Every point within the volumetric field-of-view projects a unique pseudorandom pattern of caustics on the sensor. By using a physical approximation and simple calibration scheme, we solve the large-scale inverse problem in a computationally efficient way. The caustic patterns enable compressed sensing, which exploits sparsity in the sample to solve for more 3D voxels than pixels on the 2D sensor. Our 3D voxel grid is chosen to match the experimentally measured two-point optical resolution across the field-of-view, resulting in 100 million voxels being reconstructed from a single 1.3 megapixel image. However, the effective resolution varies significantly with scene content. Because this effect is common to a wide range of computational cameras, we provide new theory for analyzing resolution in such systems.

Learning Convex Regularizers for Optimal Bayesian Denoising

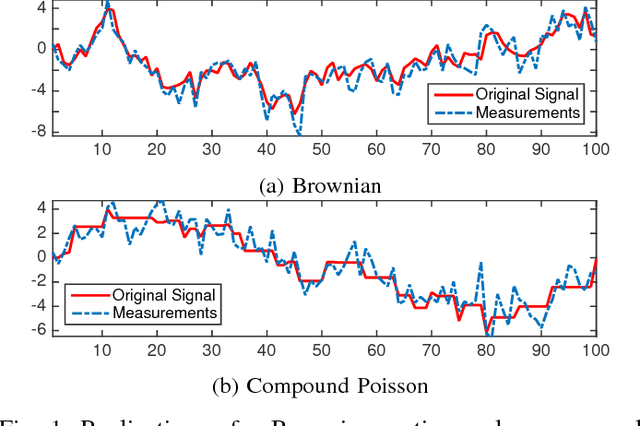
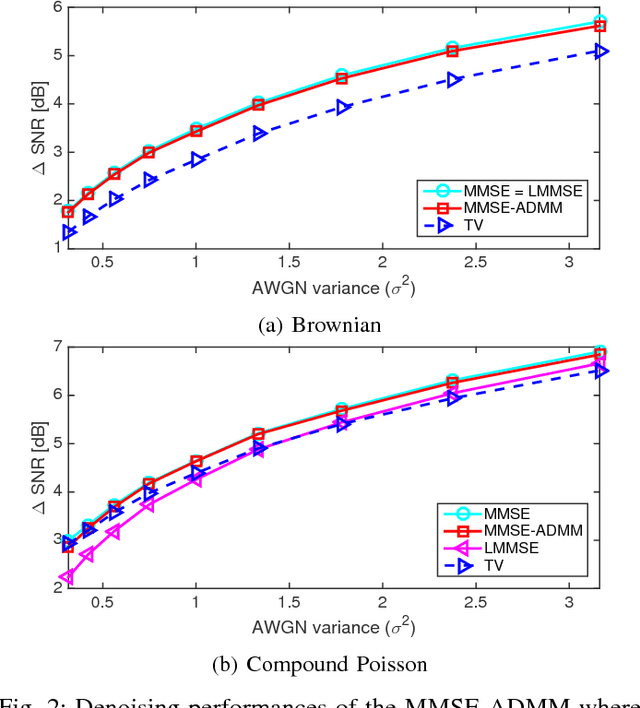
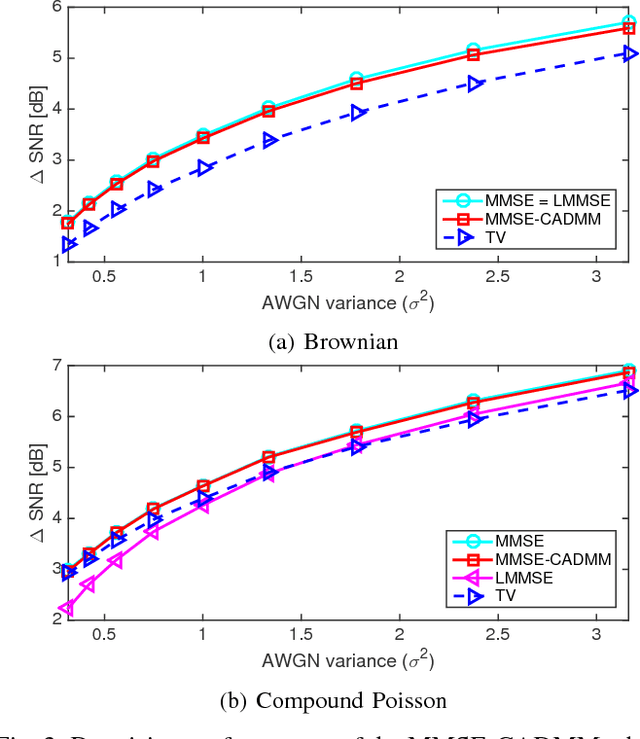
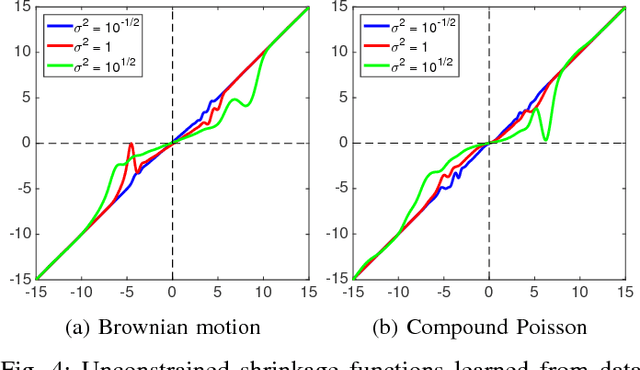
We propose a data-driven algorithm for the maximum a posteriori (MAP) estimation of stochastic processes from noisy observations. The primary statistical properties of the sought signal is specified by the penalty function (i.e., negative logarithm of the prior probability density function). Our alternating direction method of multipliers (ADMM)-based approach translates the estimation task into successive applications of the proximal mapping of the penalty function. Capitalizing on this direct link, we define the proximal operator as a parametric spline curve and optimize the spline coefficients by minimizing the average reconstruction error for a given training set. The key aspects of our learning method are that the associated penalty function is constrained to be convex and the convergence of the ADMM iterations is proven. As a result of these theoretical guarantees, adaptation of the proposed framework to different levels of measurement noise is extremely simple and does not require any retraining. We apply our method to estimation of both sparse and non-sparse models of L\'{e}vy processes for which the minimum mean square error (MMSE) estimators are available. We carry out a single training session and perform comparisons at various signal-to-noise ratio (SNR) values. Simulations illustrate that the performance of our algorithm is practically identical to the one of the MMSE estimator irrespective of the noise power.

Bayesian Estimation for Continuous-Time Sparse Stochastic Processes

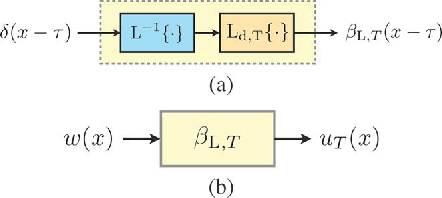
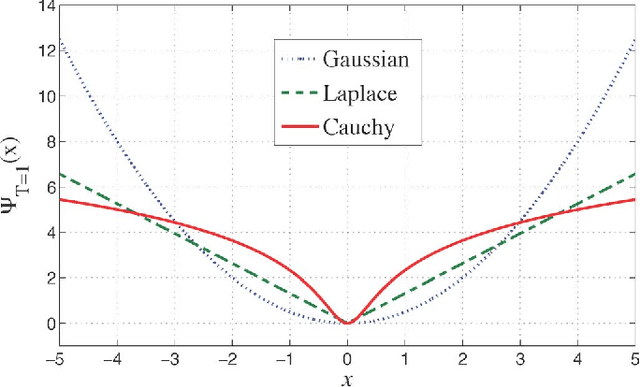
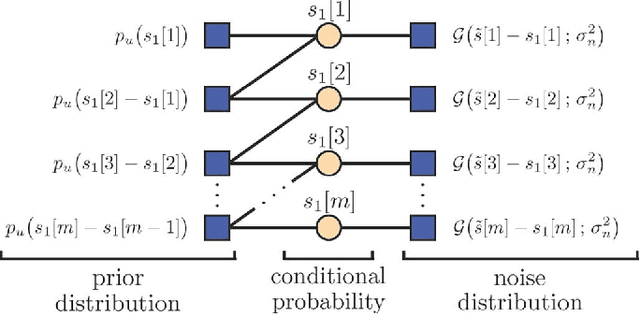
We consider continuous-time sparse stochastic processes from which we have only a finite number of noisy/noiseless samples. Our goal is to estimate the noiseless samples (denoising) and the signal in-between (interpolation problem). By relying on tools from the theory of splines, we derive the joint a priori distribution of the samples and show how this probability density function can be factorized. The factorization enables us to tractably implement the maximum a posteriori and minimum mean-square error (MMSE) criteria as two statistical approaches for estimating the unknowns. We compare the derived statistical methods with well-known techniques for the recovery of sparse signals, such as the $\ell_1$ norm and Log ($\ell_1$-$\ell_0$ relaxation) regularization methods. The simulation results show that, under certain conditions, the performance of the regularization techniques can be very close to that of the MMSE estimator.