Memory-efficient Learning for Large-scale Computational Imaging
Paper and Code
Mar 11, 2020
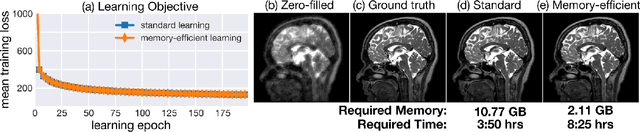
Critical aspects of computational imaging systems, such as experimental design and image priors, can be optimized through deep networks formed by the unrolled iterations of classical model-based reconstructions (termed physics-based networks). However, for real-world large-scale inverse problems, computing gradients via backpropagation is infeasible due to memory limitations of graphics processing units. In this work, we propose a memory-efficient learning procedure that exploits the reversibility of the network's layers to enable data-driven design for large-scale computational imaging systems. We demonstrate our method on a small-scale compressed sensing example, as well as two large-scale real-world systems: multi-channel magnetic resonance imaging and super-resolution optical microscopy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge