Bayesian Estimation for Continuous-Time Sparse Stochastic Processes
Paper and Code
Oct 19, 2012
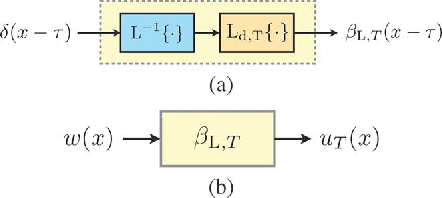
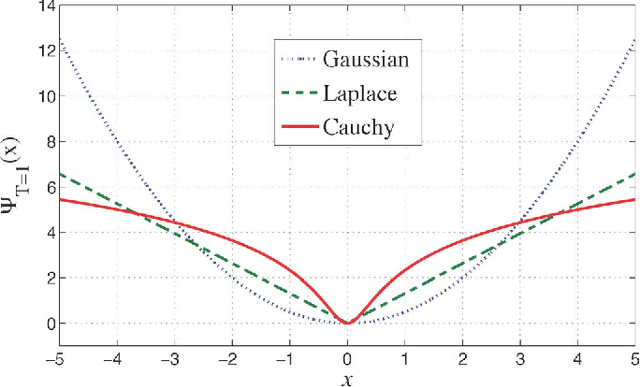
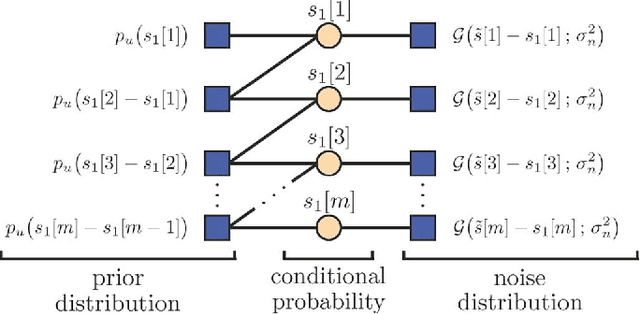
We consider continuous-time sparse stochastic processes from which we have only a finite number of noisy/noiseless samples. Our goal is to estimate the noiseless samples (denoising) and the signal in-between (interpolation problem). By relying on tools from the theory of splines, we derive the joint a priori distribution of the samples and show how this probability density function can be factorized. The factorization enables us to tractably implement the maximum a posteriori and minimum mean-square error (MMSE) criteria as two statistical approaches for estimating the unknowns. We compare the derived statistical methods with well-known techniques for the recovery of sparse signals, such as the $\ell_1$ norm and Log ($\ell_1$-$\ell_0$ relaxation) regularization methods. The simulation results show that, under certain conditions, the performance of the regularization techniques can be very close to that of the MMSE estimator.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge