Learning-based Image Reconstruction via Parallel Proximal Algorithm
Paper and Code
Jan 29, 2018
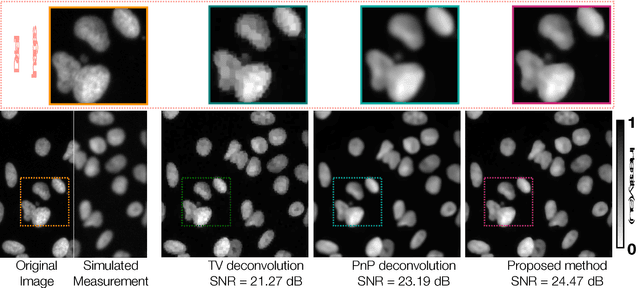
In the past decade, sparsity-driven regularization has led to advancement of image reconstruction algorithms. Traditionally, such regularizers rely on analytical models of sparsity (e.g. total variation (TV)). However, more recent methods are increasingly centered around data-driven arguments inspired by deep learning. In this letter, we propose to generalize TV regularization by replacing the l1-penalty with an alternative prior that is trainable. Specifically, our method learns the prior via extending the recently proposed fast parallel proximal algorithm (FPPA) to incorporate data-adaptive proximal operators. The proposed framework does not require additional inner iterations for evaluating the proximal mappings of the corresponding learned prior. Moreover, our formalism ensures that the training and reconstruction processes share the same algorithmic structure, making the end-to-end implementation intuitive. As an example, we demonstrate our algorithm on the problem of deconvolution in a fluorescence microscope.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge