Training Hybrid Neural Networks with Multimode Optical Nonlinearities Using Digital Twins

The ability to train ever-larger neural networks brings artificial intelligence to the forefront of scientific and technical discoveries. However, their exponentially increasing size creates a proportionally greater demand for energy and computational hardware. Incorporating complex physical events in networks as fixed, efficient computation modules can address this demand by decreasing the complexity of trainable layers. Here, we utilize ultrashort pulse propagation in multimode fibers, which perform large-scale nonlinear transformations, for this purpose. Training the hybrid architecture is achieved through a neural model that differentiably approximates the optical system. The training algorithm updates the neural simulator and backpropagates the error signal over this proxy to optimize layers preceding the optical one. Our experimental results achieve state-of-the-art image classification accuracies and simulation fidelity. Moreover, the framework demonstrates exceptional resilience to experimental drifts. By integrating low-energy physical systems into neural networks, this approach enables scalable, energy-efficient AI models with significantly reduced computational demands.

Optical Diffusion Models for Image Generation

Diffusion models generate new samples by progressively decreasing the noise from the initially provided random distribution. This inference procedure generally utilizes a trained neural network numerous times to obtain the final output, creating significant latency and energy consumption on digital electronic hardware such as GPUs. In this study, we demonstrate that the propagation of a light beam through a semi-transparent medium can be programmed to implement a denoising diffusion model on image samples. This framework projects noisy image patterns through passive diffractive optical layers, which collectively only transmit the predicted noise term in the image. The optical transparent layers, which are trained with an online training approach, backpropagating the error to the analytical model of the system, are passive and kept the same across different steps of denoising. Hence this method enables high-speed image generation with minimal power consumption, benefiting from the bandwidth and energy efficiency of optical information processing.

Training of Physical Neural Networks

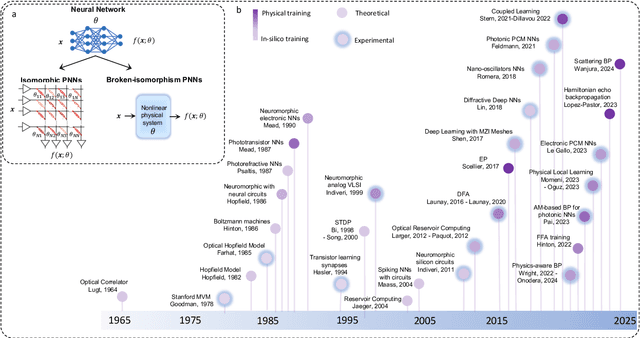
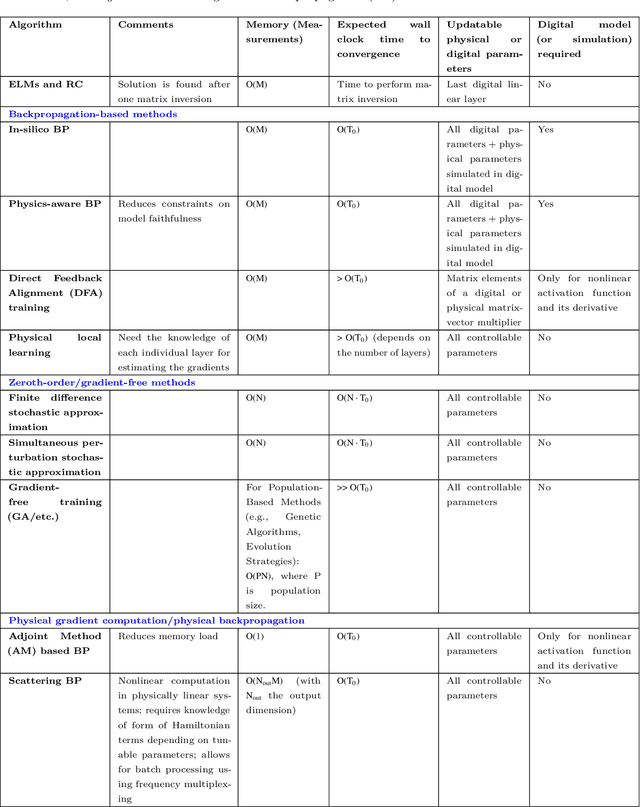
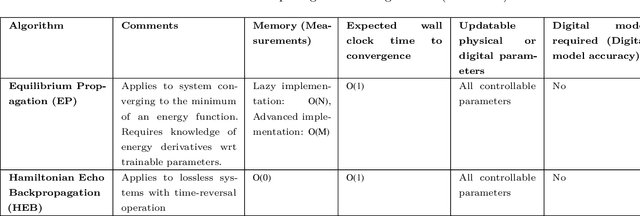
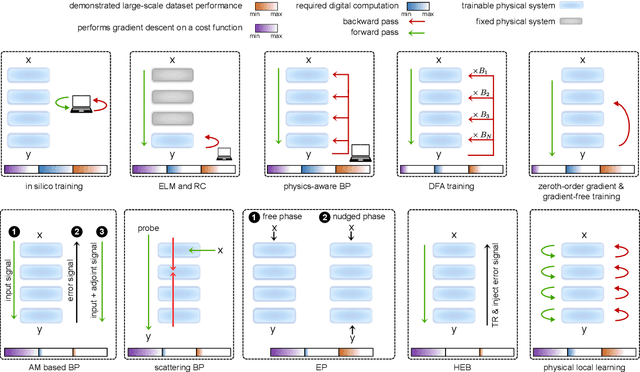
Physical neural networks (PNNs) are a class of neural-like networks that leverage the properties of physical systems to perform computation. While PNNs are so far a niche research area with small-scale laboratory demonstrations, they are arguably one of the most underappreciated important opportunities in modern AI. Could we train AI models 1000x larger than current ones? Could we do this and also have them perform inference locally and privately on edge devices, such as smartphones or sensors? Research over the past few years has shown that the answer to all these questions is likely "yes, with enough research": PNNs could one day radically change what is possible and practical for AI systems. To do this will however require rethinking both how AI models work, and how they are trained - primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs at large scale, many methods including backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs, and so far no method has been shown to scale to the same scale and performance as the backpropagation algorithm widely used in deep learning today. However, this is rapidly changing, and a diverse ecosystem of training techniques provides clues for how PNNs may one day be utilized to create both more efficient realizations of current-scale AI models, and to enable unprecedented-scale models.

Subwavelength Imaging using a Solid-Immersion Diffractive Optical Processor

Phase imaging is widely used in biomedical imaging, sensing, and material characterization, among other fields. However, direct imaging of phase objects with subwavelength resolution remains a challenge. Here, we demonstrate subwavelength imaging of phase and amplitude objects based on all-optical diffractive encoding and decoding. To resolve subwavelength features of an object, the diffractive imager uses a thin, high-index solid-immersion layer to transmit high-frequency information of the object to a spatially-optimized diffractive encoder, which converts/encodes high-frequency information of the input into low-frequency spatial modes for transmission through air. The subsequent diffractive decoder layers (in air) are jointly designed with the encoder using deep-learning-based optimization, and communicate with the encoder layer to create magnified images of input objects at its output, revealing subwavelength features that would otherwise be washed away due to diffraction limit. We demonstrate that this all-optical collaboration between a diffractive solid-immersion encoder and the following decoder layers in air can resolve subwavelength phase and amplitude features of input objects in a highly compact design. To experimentally demonstrate its proof-of-concept, we used terahertz radiation and developed a fabrication method for creating monolithic multi-layer diffractive processors. Through these monolithically fabricated diffractive encoder-decoder pairs, we demonstrated phase-to-intensity transformations and all-optically reconstructed subwavelength phase features of input objects by directly transforming them into magnified intensity features at the output. This solid-immersion-based diffractive imager, with its compact and cost-effective design, can find wide-ranging applications in bioimaging, endoscopy, sensing and materials characterization.

Nonlinear Processing with Linear Optics

Deep neural networks have achieved remarkable breakthroughs by leveraging multiple layers of data processing to extract hidden representations, albeit at the cost of large electronic computing power. To enhance energy efficiency and speed, the optical implementation of neural networks aims to harness the advantages of optical bandwidth and the energy efficiency of optical interconnections. In the absence of low-power optical nonlinearities, the challenge in the implementation of multilayer optical networks lies in realizing multiple optical layers without resorting to electronic components. In this study, we present a novel framework that uses multiple scattering that is capable of synthesizing programmable linear and nonlinear transformations concurrently at low optical power by leveraging the nonlinear relationship between the scattering potential, represented by data, and the scattered field. Theoretical and experimental investigations show that repeating the data by multiple scattering enables non-linear optical computing at low power continuous wave light.

Forward-Forward Training of an Optical Neural Network

Neural networks (NN) have demonstrated remarkable capabilities in various tasks, but their computation-intensive nature demands faster and more energy-efficient hardware implementations. Optics-based platforms, using technologies such as silicon photonics and spatial light modulators, offer promising avenues for achieving this goal. However, training multiple trainable layers in tandem with these physical systems poses challenges, as they are difficult to fully characterize and describe with differentiable functions, hindering the use of error backpropagation algorithm. The recently introduced Forward-Forward Algorithm (FFA) eliminates the need for perfect characterization of the learning system and shows promise for efficient training with large numbers of programmable parameters. The FFA does not require backpropagating an error signal to update the weights, rather the weights are updated by only sending information in one direction. The local loss function for each set of trainable weights enables low-power analog hardware implementations without resorting to metaheuristic algorithms or reinforcement learning. In this paper, we present an experiment utilizing multimode nonlinear wave propagation in an optical fiber demonstrating the feasibility of the FFA approach using an optical system. The results show that incorporating optical transforms in multilayer NN architectures trained with the FFA, can lead to performance improvements, even with a relatively small number of trainable weights. The proposed method offers a new path to the challenge of training optical NNs and provides insights into leveraging physical transformations for enhancing NN performance.

Nonlinear Optical Data Transformer for Machine Learning

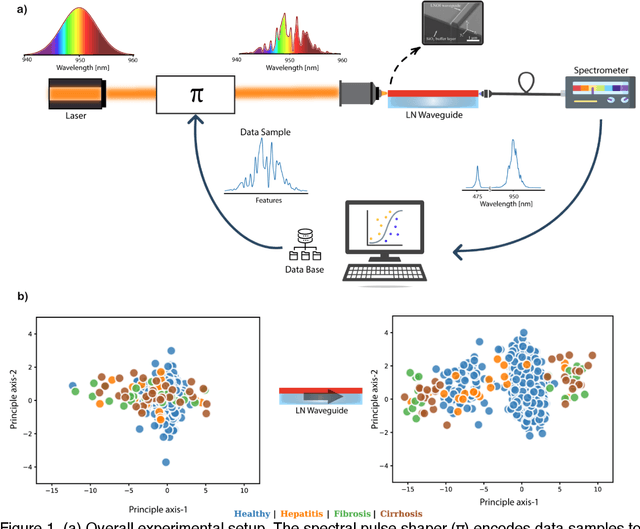
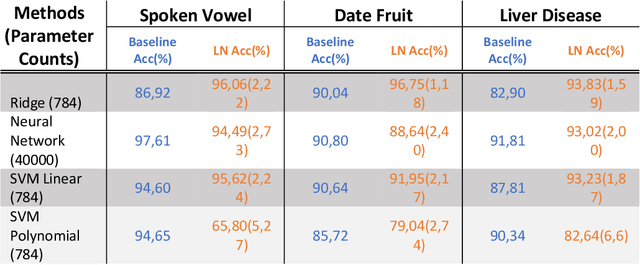
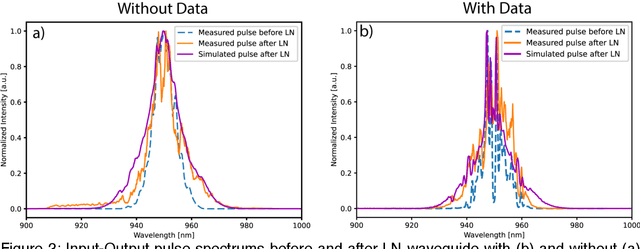
Modern machine learning models use an ever-increasing number of parameters to train (175 billion parameters for GPT-3) with large datasets to obtain better performance. Bigger is better has been the norm. Optical computing has been reawakened as a potential solution to large-scale computing through optical accelerators that carry out linear operations while reducing electrical power. However, to achieve efficient computing with light, creating and controlling nonlinearity optically rather than electronically remains a challenge. This study explores a reservoir computing (RC) approach whereby a 14 mm long few-mode waveguide in LiNbO3 on insulator is used as a complex nonlinear optical processor. A dataset is encoded digitally on the spectrum of a femtosecond pulse which is then launched in the waveguide. The output spectrum depends nonlinearly on the input. We experimentally show that a simple digital linear classifier with 784 parameters using the output spectrum from the waveguide as input increased the classification accuracy of several databases compared to non-transformed data, approximately 10$\%$. In comparison, a deep digital neural network (NN) with 40000 parameters was necessary to achieve the same accuracy. Reducing the number of parameters by a factor of $\sim$50 illustrates that a compact optical RC approach can perform on par with a deep digital NN.

Physics-informed neural networks for diffraction tomography

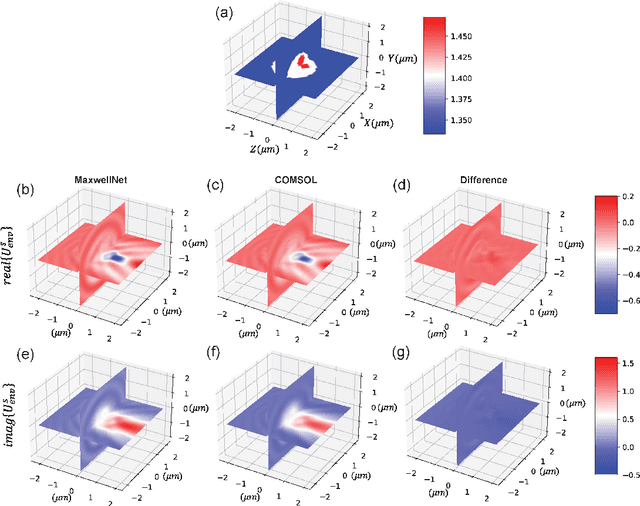
We propose a physics-informed neural network as the forward model for tomographic reconstructions of biological samples. We demonstrate that by training this network with the Helmholtz equation as a physical loss, we can predict the scattered field accurately. It will be shown that a pretrained network can be fine-tuned for different samples and used for solving the scattering problem much faster than other numerical solutions. We evaluate our methodology with numerical and experimental results. Our physics-informed neural networks can be generalized for any forward and inverse scattering problem.

Single-cell phase-contrast tomograms data encoded by 3D Zernike descriptors

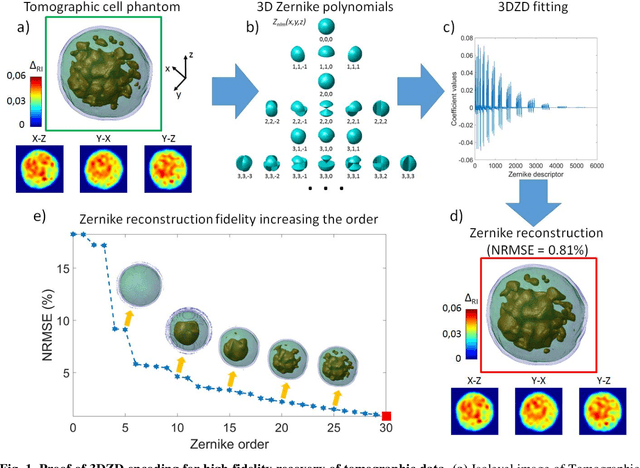
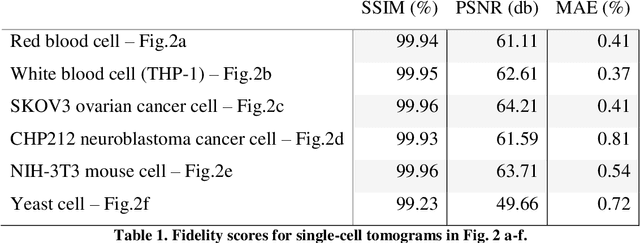
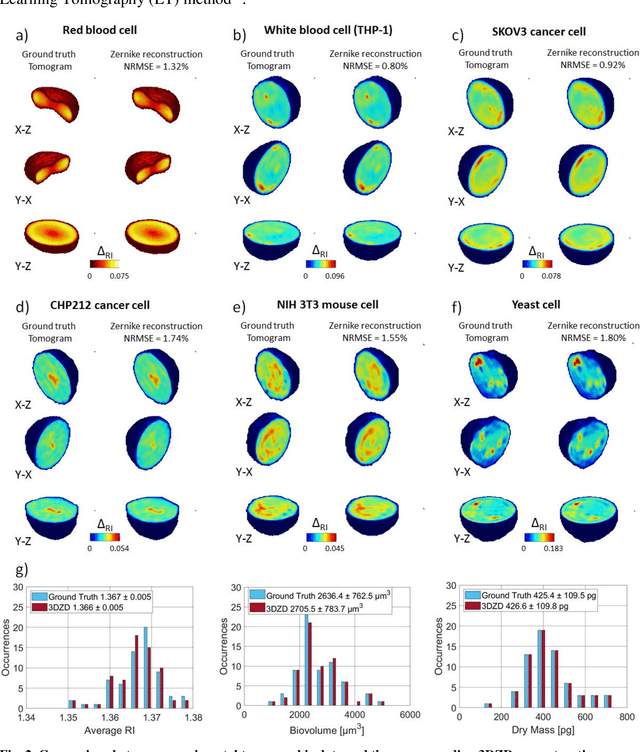
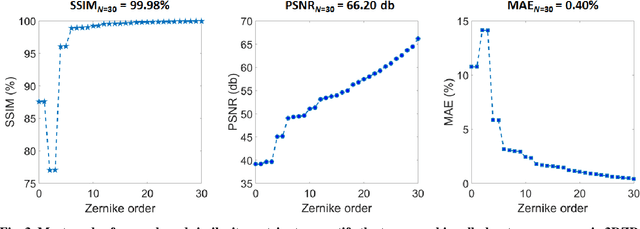
Phase-contrast tomographic flow cytometry combines quantitative 3D analysis of unstained single cells and high-throughput. A crucial issue of this method is the storage and management of the huge amount of 3D tomographic data. Here we show an effective quasi lossless compression of tomograms data through 3D Zernike descriptors, unlocking data management tasks and computational pipelines that were unattainable until now.

Optical Diffraction Tomography based on 3D Physics-Inspired Neural Network (PINN)

Optical diffraction tomography (ODT) is an emerging 3D imaging technique that is used for the 3D reconstruction of the refractive index (RI) for semi-transparent samples. Various inverse models have been proposed to reconstruct the 3D RI based on the holographic detection of different samples such as the Born and the Rytov approximations. However, such approximations usually suffer from the so-called missing-cone problem that results in an elongation of the final reconstruction along the optical axis. Different iterative schemes have been proposed to solve the missing cone problem relying on physical forward models and an error function that aims at filling in the k-space and thus eliminating the missing-cone problem and reaching better reconstruction accuracy. In this paper, we propose a different approach where a 3D neural network (NN) is employed. The NN is trained with a cost function derived from a physical model based on the physics of optical wave propagation. The 3D NN starts with an initial guess for the 3D RI reconstruction (i.e. Born, or Rytov) and aims at reconstructing better 3D reconstruction based on an error function. With this technique, the NN can be trained without any examples of the relation between the ill-posed reconstruction (Born or Rytov) and the ground truth (true shape).