Quantum Equilibrium Propagation for efficient training of quantum systems based on Onsager reciprocity

The widespread adoption of machine learning and artificial intelligence in all branches of science and technology has created a need for energy-efficient, alternative hardware platforms. While such neuromorphic approaches have been proposed and realised for a wide range of platforms, physically extracting the gradients required for training remains challenging as generic approaches only exist in certain cases. Equilibrium propagation (EP) is such a procedure that has been introduced and applied to classical energy-based models which relax to an equilibrium. Here, we show a direct connection between EP and Onsager reciprocity and exploit this to derive a quantum version of EP. This can be used to optimize loss functions that depend on the expectation values of observables of an arbitrary quantum system. Specifically, we illustrate this new concept with supervised and unsupervised learning examples in which the input or the solvable task is of quantum mechanical nature, e.g., the recognition of quantum many-body ground states, quantum phase exploration, sensing and phase boundary exploration. We propose that in the future quantum EP may be used to solve tasks such as quantum phase discovery with a quantum simulator even for Hamiltonians which are numerically hard to simulate or even partially unknown. Our scheme is relevant for a variety of quantum simulation platforms such as ion chains, superconducting qubit arrays, neutral atom Rydberg tweezer arrays and strongly interacting atoms in optical lattices.

Training of Physical Neural Networks

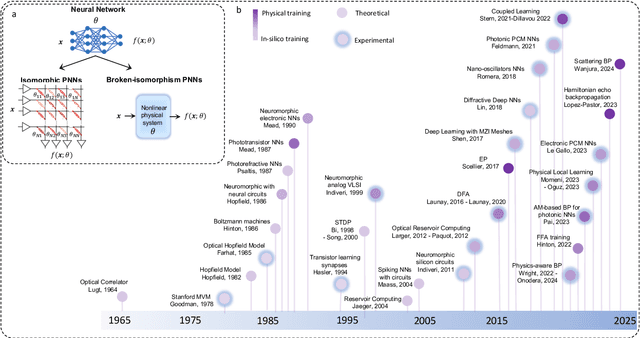
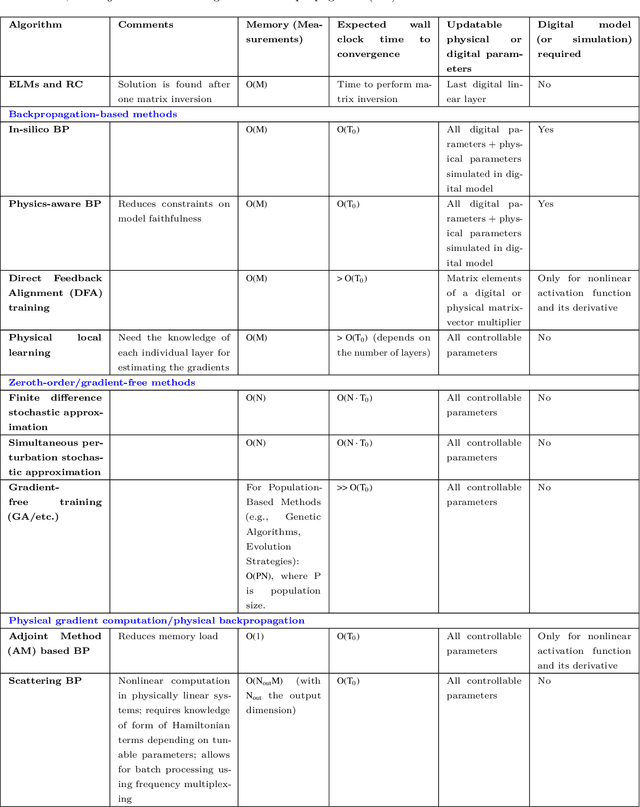
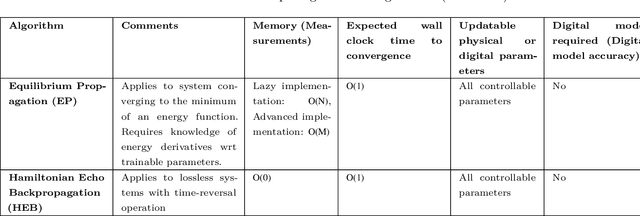
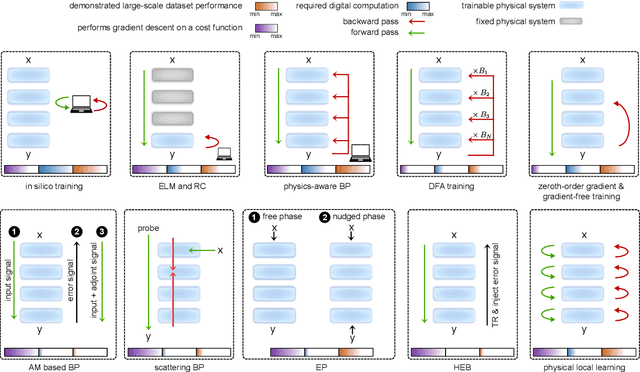
Physical neural networks (PNNs) are a class of neural-like networks that leverage the properties of physical systems to perform computation. While PNNs are so far a niche research area with small-scale laboratory demonstrations, they are arguably one of the most underappreciated important opportunities in modern AI. Could we train AI models 1000x larger than current ones? Could we do this and also have them perform inference locally and privately on edge devices, such as smartphones or sensors? Research over the past few years has shown that the answer to all these questions is likely "yes, with enough research": PNNs could one day radically change what is possible and practical for AI systems. To do this will however require rethinking both how AI models work, and how they are trained - primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs at large scale, many methods including backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs, and so far no method has been shown to scale to the same scale and performance as the backpropagation algorithm widely used in deep learning today. However, this is rapidly changing, and a diverse ecosystem of training techniques provides clues for how PNNs may one day be utilized to create both more efficient realizations of current-scale AI models, and to enable unprecedented-scale models.

Training Coupled Phase Oscillators as a Neuromorphic Platform using Equilibrium Propagation

Given the rapidly growing scale and resource requirements of machine learning applications, the idea of building more efficient learning machines much closer to the laws of physics is an attractive proposition. One central question for identifying promising candidates for such neuromorphic platforms is whether not only inference but also training can exploit the physical dynamics. In this work, we show that it is possible to successfully train a system of coupled phase oscillators - one of the most widely investigated nonlinear dynamical systems with a multitude of physical implementations, comprising laser arrays, coupled mechanical limit cycles, superfluids, and exciton-polaritons. To this end, we apply the approach of equilibrium propagation, which permits to extract training gradients via a physical realization of backpropagation, based only on local interactions. The complex energy landscape of the XY/ Kuramoto model leads to multistability, and we show how to address this challenge. Our study identifies coupled phase oscillators as a new general-purpose neuromorphic platform and opens the door towards future experimental implementations.