Schemato -- An LLM for Netlist-to-Schematic Conversion

Machine learning models are advancing circuit design, particularly in analog circuits. They typically generate netlists that lack human interpretability. This is a problem as human designers heavily rely on the interpretability of circuit diagrams or schematics to intuitively understand, troubleshoot, and develop designs. Hence, to integrate domain knowledge effectively, it is crucial to translate ML-generated netlists into interpretable schematics quickly and accurately. We propose Schemato, a large language model (LLM) for netlist-to-schematic conversion. In particular, we consider our approach in the two settings of converting netlists to .asc files for LTSpice and LATEX files for CircuiTikz schematics. Experiments on our circuit dataset show that Schemato achieves up to 93% compilation success rate for the netlist-to-LaTeX conversion task, surpassing the 26% rate scored by the state-of-the-art LLMs. Furthermore, our experiments show that Schemato generates schematics with a mean structural similarity index measure that is 3xhigher than the best performing LLMs, therefore closer to the reference human design.

GraCo -- A Graph Composer for Integrated Circuits

Designing integrated circuits involves substantial complexity, posing challenges in revealing its potential applications - from custom digital cells to analog circuits. Despite extensive research over the past decades in building versatile and automated frameworks, there remains open room to explore more computationally efficient AI-based solutions. This paper introduces the graph composer GraCo, a novel method for synthesizing integrated circuits using reinforcement learning (RL). GraCo learns to construct a graph step-by-step, which is then converted into a netlist and simulated with SPICE. We demonstrate that GraCo is highly configurable, enabling the incorporation of prior design knowledge into the framework. We formalize how this prior knowledge can be utilized and, in particular, show that applying consistency checks enhances the efficiency of the sampling process. To evaluate its performance, we compare GraCo to a random baseline, which is known to perform well for smaller design space problems. We demonstrate that GraCo can discover circuits for tasks such as generating standard cells, including the inverter and the two-input NAND (NAND2) gate. Compared to a random baseline, GraCo requires 5x fewer sampling steps to design an inverter and successfully synthesizes a NAND2 gate that is 2.5x faster.

Training of Physical Neural Networks

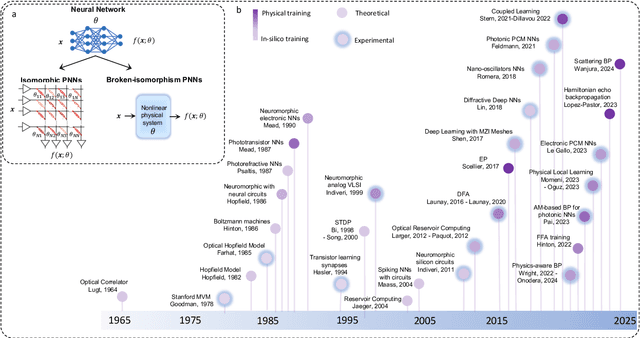
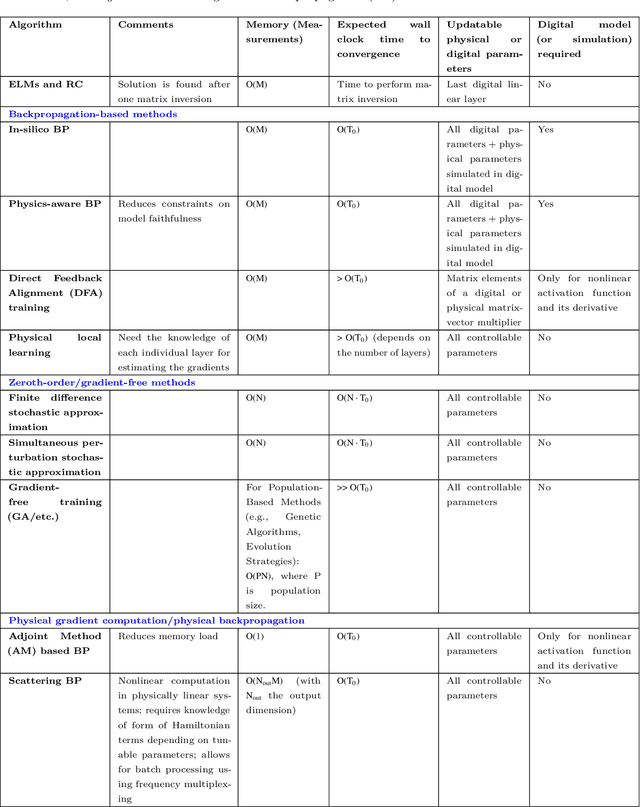
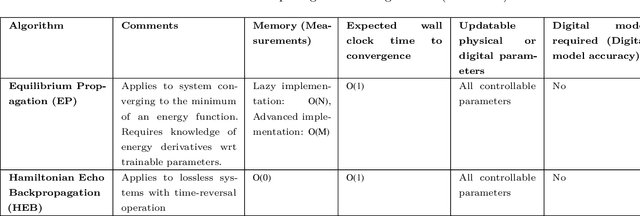
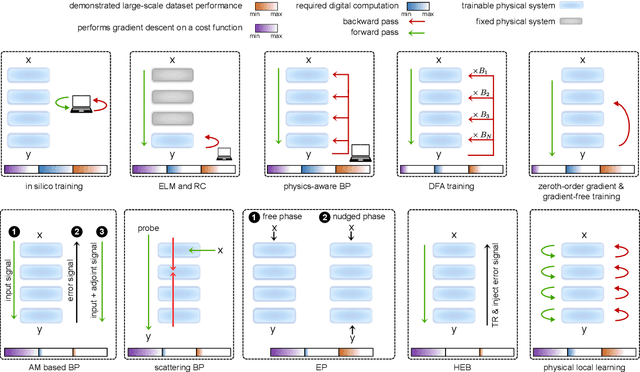
Physical neural networks (PNNs) are a class of neural-like networks that leverage the properties of physical systems to perform computation. While PNNs are so far a niche research area with small-scale laboratory demonstrations, they are arguably one of the most underappreciated important opportunities in modern AI. Could we train AI models 1000x larger than current ones? Could we do this and also have them perform inference locally and privately on edge devices, such as smartphones or sensors? Research over the past few years has shown that the answer to all these questions is likely "yes, with enough research": PNNs could one day radically change what is possible and practical for AI systems. To do this will however require rethinking both how AI models work, and how they are trained - primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs at large scale, many methods including backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs, and so far no method has been shown to scale to the same scale and performance as the backpropagation algorithm widely used in deep learning today. However, this is rapidly changing, and a diverse ecosystem of training techniques provides clues for how PNNs may one day be utilized to create both more efficient realizations of current-scale AI models, and to enable unprecedented-scale models.

Backpropagation-free Training of Deep Physical Neural Networks

Recent years have witnessed the outstanding success of deep learning in various fields such as vision and natural language processing. This success is largely indebted to the massive size of deep learning models that is expected to increase unceasingly. This growth of the deep learning models is accompanied by issues related to their considerable energy consumption, both during the training and inference phases, as well as their scalability. Although a number of work based on unconventional physical systems have been proposed which addresses the issue of energy efficiency in the inference phase, efficient training of deep learning models has remained unaddressed. So far, training of digital deep learning models mainly relies on backpropagation, which is not suitable for physical implementation as it requires perfect knowledge of the computation performed in the so-called forward pass of the neural network. Here, we tackle this issue by proposing a simple deep neural network architecture augmented by a biologically plausible learning algorithm, referred to as "model-free forward-forward training". The proposed architecture enables training deep physical neural networks consisting of layers of physical nonlinear systems, without requiring detailed knowledge of the nonlinear physical layers' properties. We show that our method outperforms state-of-the-art hardware-aware training methods by improving training speed, decreasing digital computations, and reducing power consumption in physical systems. We demonstrate the adaptability of the proposed method, even in systems exposed to dynamic or unpredictable external perturbations. To showcase the universality of our approach, we train diverse wave-based physical neural networks that vary in the underlying wave phenomenon and the type of non-linearity they use, to perform vowel and image classification tasks experimentally.

Physics-inspired Neuroacoustic Computing Based on Tunable Nonlinear Multiple-scattering

Waves, such as light and sound, inherently bounce and mix due to multiple scattering induced by the complex material objects that surround us. This scattering process severely scrambles the information carried by waves, challenging conventional communication systems, sensing paradigms, and wave-based computing schemes. Here, we show that instead of being a hindrance, multiple scattering can be beneficial to enable and enhance analog nonlinear information mapping, allowing for the direct physical implementation of computational paradigms such as reservoir computing and extreme learning machines. We propose a physics-inspired version of such computational architectures for speech and vowel recognition that operate directly in the native domain of the input signal, namely on real-sounds, without any digital pre-processing or encoding conversion and backpropagation training computation. We first implement it in a proof-of-concept prototype, a nonlinear chaotic acoustic cavity containing multiple tunable and power-efficient nonlinear meta-scatterers. We prove the efficiency of the acoustic-based computing system for vowel recognition tasks with high testing classification accuracy (91.4%). Finally, we demonstrate the high performance of vowel recognition in the natural environment of a reverberation room. Our results open the way for efficient acoustic learning machines that operate directly on the input sound, and leverage physics to enable Natural Language Processing (NLP).

Wave-based extreme deep learning based on non-linear time-Floquet entanglement

Wave-based analog signal processing holds the promise of extremely fast, on-the-fly, power-efficient data processing, occurring as a wave propagates through an artificially engineered medium. Yet, due to the fundamentally weak non-linearities of traditional wave materials, such analog processors have been so far largely confined to simple linear projections such as image edge detection or matrix multiplications. Complex neuromorphic computing tasks, which inherently require strong non-linearities, have so far remained out-of-reach of wave-based solutions, with a few attempts that implemented non-linearities on the digital front, or used weak and inflexible non-linear sensors, restraining the learning performance. Here, we tackle this issue by demonstrating the relevance of Time-Floquet physics to induce a strong non-linear entanglement between signal inputs at different frequencies, enabling a power-efficient and versatile wave platform for analog extreme deep learning involving a single, uniformly modulated dielectric layer and a scattering medium. We prove the efficiency of the method for extreme learning machines and reservoir computing to solve a range of challenging learning tasks, from forecasting chaotic time series to the simultaneous classification of distinct datasets. Our results open the way for wave-based machine learning with high energy efficiency, speed, and scalability.