Training of Physical Neural Networks

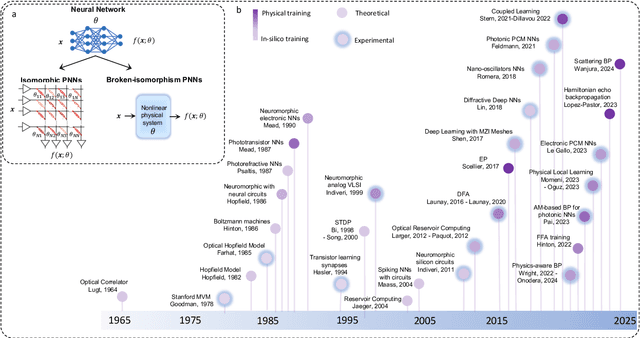
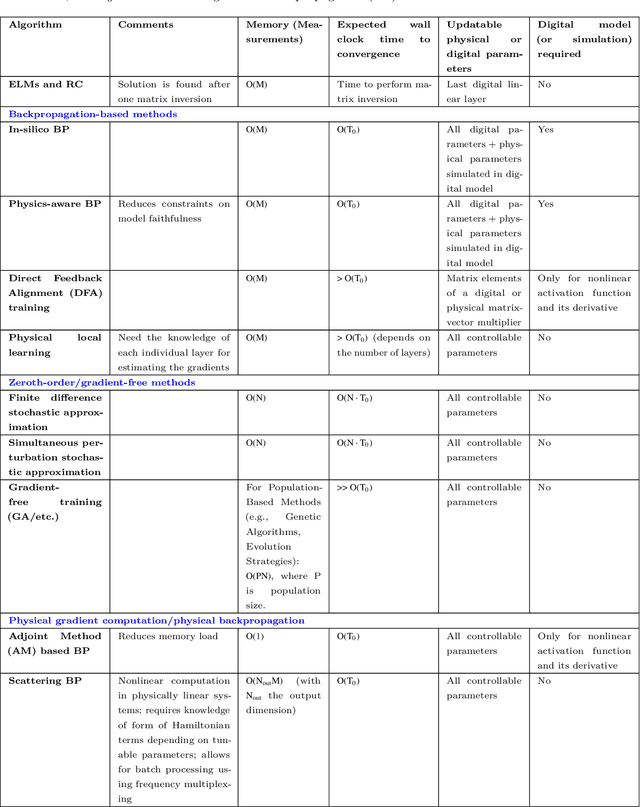
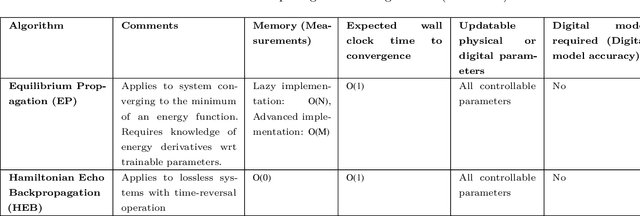
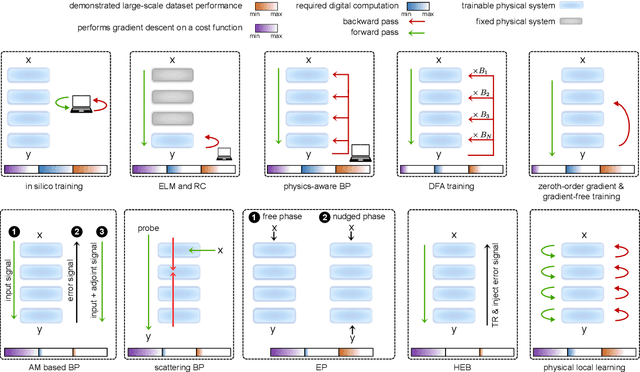
Physical neural networks (PNNs) are a class of neural-like networks that leverage the properties of physical systems to perform computation. While PNNs are so far a niche research area with small-scale laboratory demonstrations, they are arguably one of the most underappreciated important opportunities in modern AI. Could we train AI models 1000x larger than current ones? Could we do this and also have them perform inference locally and privately on edge devices, such as smartphones or sensors? Research over the past few years has shown that the answer to all these questions is likely "yes, with enough research": PNNs could one day radically change what is possible and practical for AI systems. To do this will however require rethinking both how AI models work, and how they are trained - primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs at large scale, many methods including backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs, and so far no method has been shown to scale to the same scale and performance as the backpropagation algorithm widely used in deep learning today. However, this is rapidly changing, and a diverse ecosystem of training techniques provides clues for how PNNs may one day be utilized to create both more efficient realizations of current-scale AI models, and to enable unprecedented-scale models.

Scaling on-chip photonic neural processors using arbitrarily programmable wave propagation

On-chip photonic processors for neural networks have potential benefits in both speed and energy efficiency but have not yet reached the scale at which they can outperform electronic processors. The dominant paradigm for designing on-chip photonics is to make networks of relatively bulky discrete components connected by one-dimensional waveguides. A far more compact alternative is to avoid explicitly defining any components and instead sculpt the continuous substrate of the photonic processor to directly perform the computation using waves freely propagating in two dimensions. We propose and demonstrate a device whose refractive index as a function of space, $n(x,z)$, can be rapidly reprogrammed, allowing arbitrary control over the wave propagation in the device. Our device, a 2D-programmable waveguide, combines photoconductive gain with the electro-optic effect to achieve massively parallel modulation of the refractive index of a slab waveguide, with an index modulation depth of $10^{-3}$ and approximately $10^4$ programmable degrees of freedom. We used a prototype device with a functional area of $12\,\text{mm}^2$ to perform neural-network inference with up to 49-dimensional input vectors in a single pass, achieving 96% accuracy on vowel classification and 86% accuracy on $7 \times 7$-pixel MNIST handwritten-digit classification. This is a scale beyond that of previous photonic chips relying on discrete components, illustrating the benefit of the continuous-waves paradigm. In principle, with large enough chip area, the reprogrammability of the device's refractive index distribution enables the reconfigurable realization of any passive, linear photonic circuit or device. This promises the development of more compact and versatile photonic systems for a wide range of applications, including optical processing, smart sensing, spectroscopy, and optical communications.

The hardware is the software

Human brains and bodies are not hardware running software: the hardware is the software. We reason that because the microscopic physics of artificial-intelligence hardware and of human biological "hardware" is distinct, neuromorphic engineers need to be cautious (and yet also creative) in how we take inspiration from biological intelligence. We should focus primarily on principles and design ideas that respect -- and embrace -- the underlying hardware physics of non-biological intelligent systems, rather than abstracting it away. We see a major role for neuroscience in neuromorphic computing as identifying the physics-agnostic principles of biological intelligence -- that is the principles of biological intelligence that can be gainfully adapted and applied to any physical hardware.

Quantum-noise-limited optical neural networks operating at a few quanta per activation

Analog physical neural networks, which hold promise for improved energy efficiency and speed compared to digital electronic neural networks, are nevertheless typically operated in a relatively high-power regime so that the signal-to-noise ratio (SNR) is large (>10). What happens if an analog system is instead operated in an ultra-low-power regime, in which the behavior of the system becomes highly stochastic and the noise is no longer a small perturbation on the signal? In this paper, we study this question in the setting of optical neural networks operated in the limit where some layers use only a single photon to cause a neuron activation. Neuron activations in this limit are dominated by quantum noise from the fundamentally probabilistic nature of single-photon detection of weak optical signals. We show that it is possible to train stochastic optical neural networks to perform deterministic image-classification tasks with high accuracy in spite of the extremely high noise (SNR ~ 1) by using a training procedure that directly models the stochastic behavior of photodetection. We experimentally demonstrated MNIST classification with a test accuracy of 98% using an optical neural network with a hidden layer operating in the single-photon regime; the optical energy used to perform the classification corresponds to 0.008 photons per multiply-accumulate (MAC) operation, which is equivalent to 0.003 attojoules of optical energy per MAC. Our experiment used >40x fewer photons per inference than previous state-of-the-art low-optical-energy demonstrations, to achieve the same accuracy of >90%. Our work shows that some extremely stochastic analog systems, including those operating in the limit where quantum noise dominates, can nevertheless be used as layers in neural networks that deterministically perform classification tasks with high accuracy if they are appropriately trained.

Optical Transformers

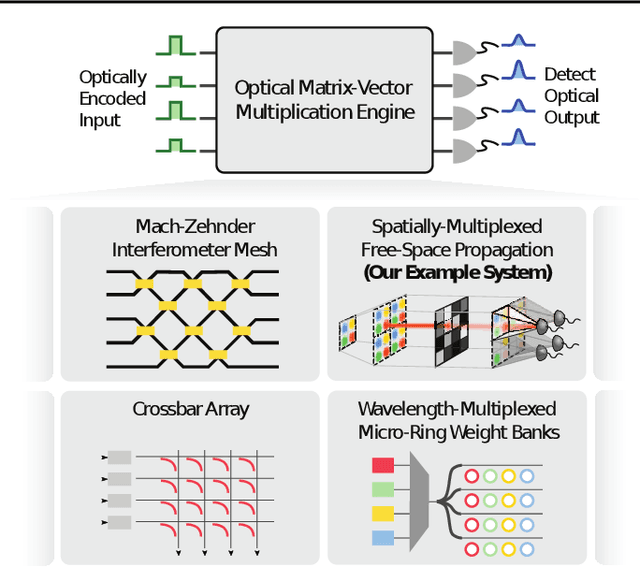
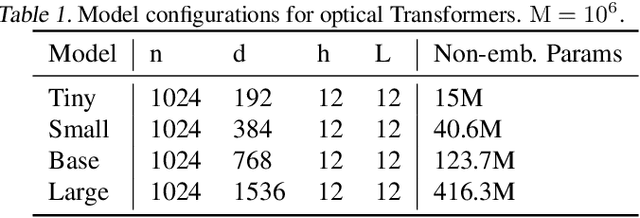
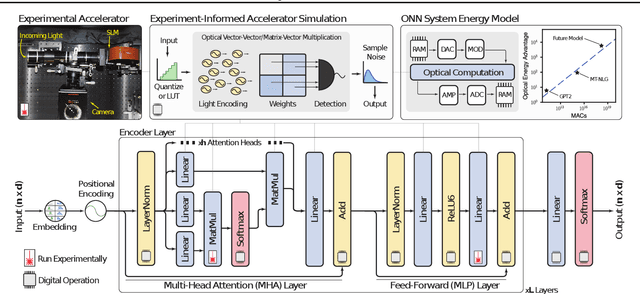
The rapidly increasing size of deep-learning models has caused renewed and growing interest in alternatives to digital computers to dramatically reduce the energy cost of running state-of-the-art neural networks. Optical matrix-vector multipliers are best suited to performing computations with very large operands, which suggests that large Transformer models could be a good target for optical computing. To test this idea, we performed small-scale optical experiments with a prototype accelerator to demonstrate that Transformer operations can run on optical hardware despite noise and errors. Using simulations, validated by our experiments, we then explored the energy efficiency of optical implementations of Transformers and identified scaling laws for model performance with respect to optical energy usage. We found that the optical energy per multiply-accumulate (MAC) scales as $\frac{1}{d}$ where $d$ is the Transformer width, an asymptotic advantage over digital systems. We conclude that with well-engineered, large-scale optical hardware, it may be possible to achieve a $100 \times$ energy-efficiency advantage for running some of the largest current Transformer models, and that if both the models and the optical hardware are scaled to the quadrillion-parameter regime, optical computers could have a $>8,000\times$ energy-efficiency advantage over state-of-the-art digital-electronic processors that achieve 300 fJ/MAC. We analyzed how these results motivate and inform the construction of future optical accelerators along with optics-amenable deep-learning approaches. With assumptions about future improvements to electronics and Transformer quantization techniques (5$\times$ cheaper memory access, double the digital--analog conversion efficiency, and 4-bit precision), we estimated that optical computers' advantage against current 300-fJ/MAC digital processors could grow to $>100,000\times$.

Image sensing with multilayer, nonlinear optical neural networks

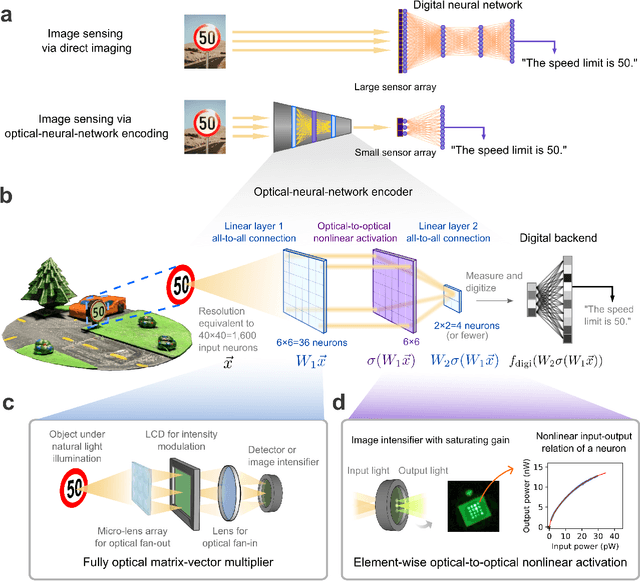
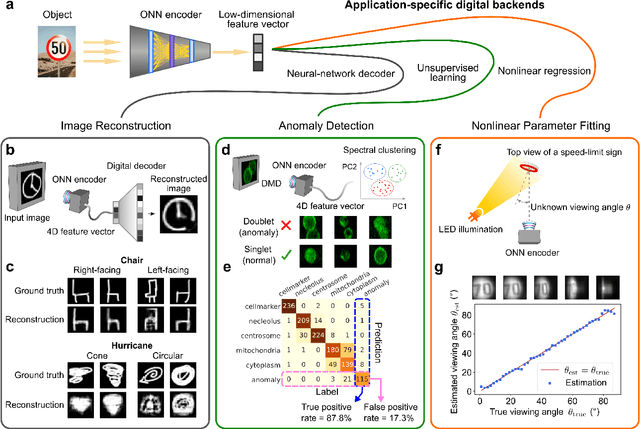
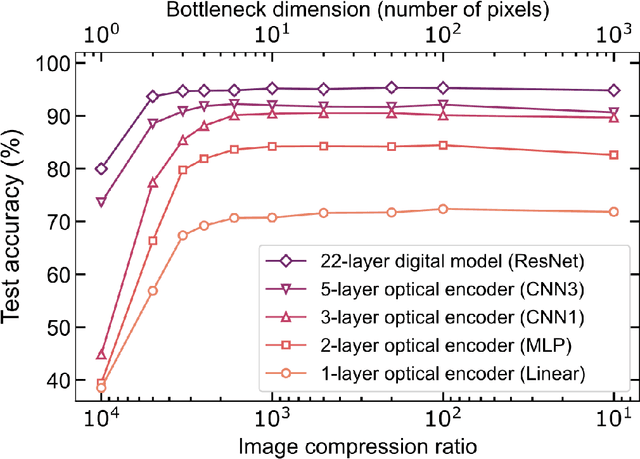
Optical imaging is commonly used for both scientific and technological applications across industry and academia. In image sensing, a measurement, such as of an object's position, is performed by computational analysis of a digitized image. An emerging image-sensing paradigm breaks this delineation between data collection and analysis by designing optical components to perform not imaging, but encoding. By optically encoding images into a compressed, low-dimensional latent space suitable for efficient post-analysis, these image sensors can operate with fewer pixels and fewer photons, allowing higher-throughput, lower-latency operation. Optical neural networks (ONNs) offer a platform for processing data in the analog, optical domain. ONN-based sensors have however been limited to linear processing, but nonlinearity is a prerequisite for depth, and multilayer NNs significantly outperform shallow NNs on many tasks. Here, we realize a multilayer ONN pre-processor for image sensing, using a commercial image intensifier as a parallel optoelectronic, optical-to-optical nonlinear activation function. We demonstrate that the nonlinear ONN pre-processor can achieve compression ratios of up to 800:1 while still enabling high accuracy across several representative computer-vision tasks, including machine-vision benchmarks, flow-cytometry image classification, and identification of objects in real scenes. In all cases we find that the ONN's nonlinearity and depth allowed it to outperform a purely linear ONN encoder. Although our experiments are specialized to ONN sensors for incoherent-light images, alternative ONN platforms should facilitate a range of ONN sensors. These ONN sensors may surpass conventional sensors by pre-processing optical information in spatial, temporal, and/or spectral dimensions, potentially with coherent and quantum qualities, all natively in the optical domain.

An optical neural network using less than 1 photon per multiplication

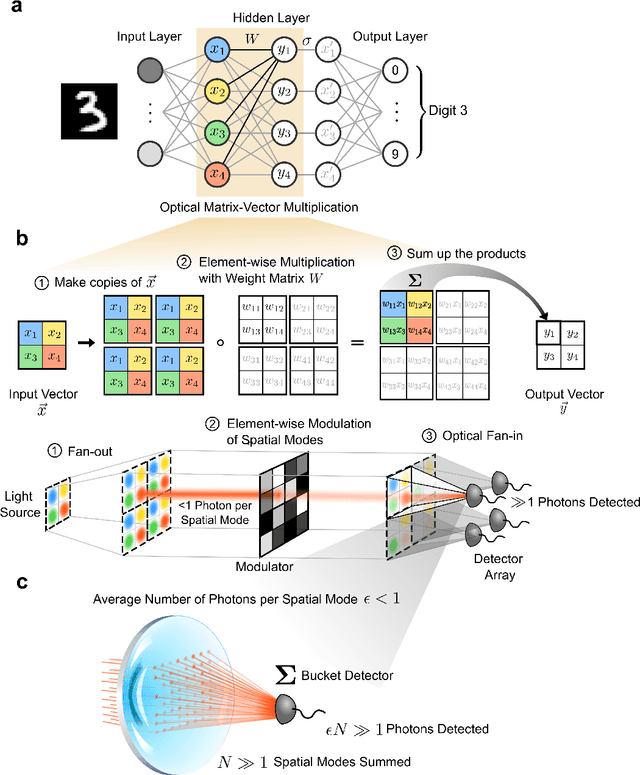
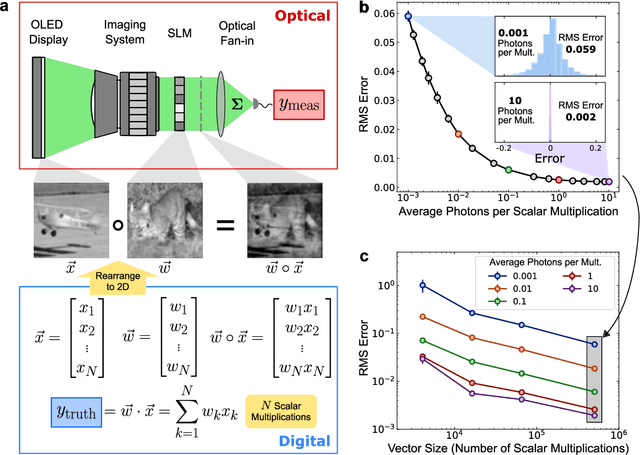
Deep learning has rapidly become a widespread tool in both scientific and commercial endeavors. Milestones of deep learning exceeding human performance have been achieved for a growing number of tasks over the past several years, across areas as diverse as game-playing, natural-language translation, and medical-image analysis. However, continued progress is increasingly hampered by the high energy costs associated with training and running deep neural networks on electronic processors. Optical neural networks have attracted attention as an alternative physical platform for deep learning, as it has been theoretically predicted that they can fundamentally achieve higher energy efficiency than neural networks deployed on conventional digital computers. Here, we experimentally demonstrate an optical neural network achieving 99% accuracy on handwritten-digit classification using ~3.2 detected photons per weight multiplication and ~90% accuracy using ~0.64 photons (~$2.4 \times 10^{-19}$ J of optical energy) per weight multiplication. This performance was achieved using a custom free-space optical processor that executes matrix-vector multiplications in a massively parallel fashion, with up to ~0.5 million scalar (weight) multiplications performed at the same time. Using commercially available optical components and standard neural-network training methods, we demonstrated that optical neural networks can operate near the standard quantum limit with extremely low optical powers and still achieve high accuracy. Our results provide a proof-of-principle for low-optical-power operation, and with careful system design including the surrounding electronics used for data storage and control, open up a path to realizing optical processors that require only $10^{-16}$ J total energy per scalar multiplication -- which is orders of magnitude more efficient than current digital processors.

Deep physical neural networks enabled by a backpropagation algorithm for arbitrary physical systems

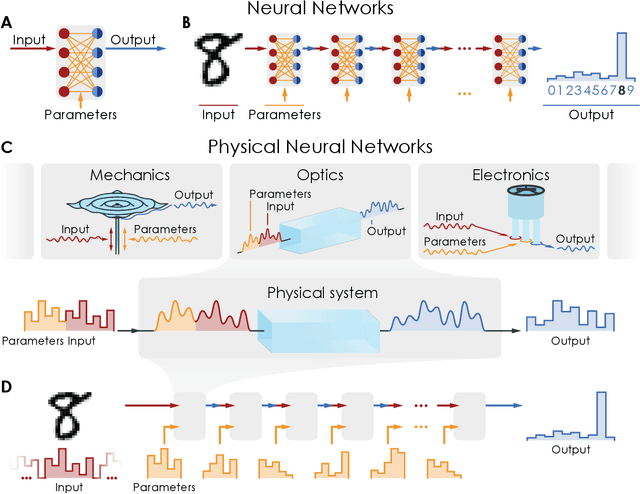
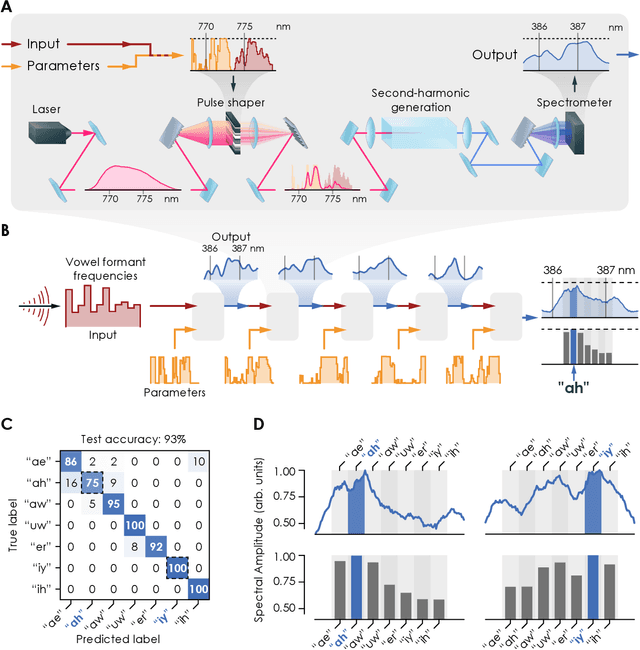
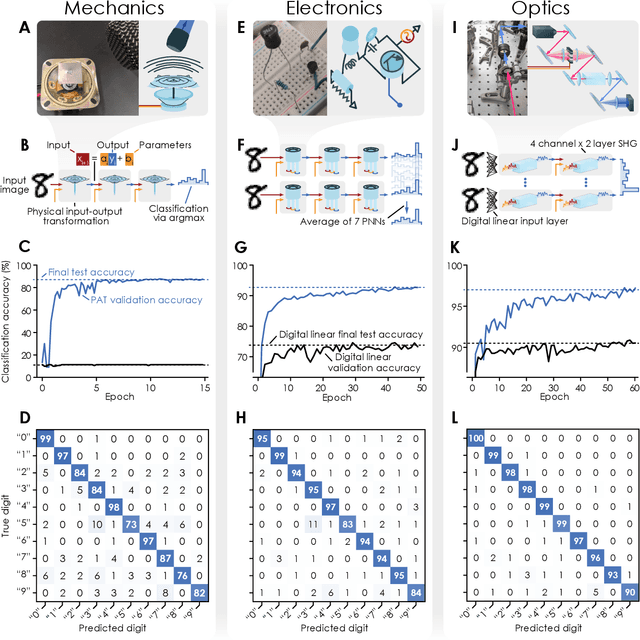
Deep neural networks have become a pervasive tool in science and engineering. However, modern deep neural networks' growing energy requirements now increasingly limit their scaling and broader use. We propose a radical alternative for implementing deep neural network models: Physical Neural Networks. We introduce a hybrid physical-digital algorithm called Physics-Aware Training to efficiently train sequences of controllable physical systems to act as deep neural networks. This method automatically trains the functionality of any sequence of real physical systems, directly, using backpropagation, the same technique used for modern deep neural networks. To illustrate their generality, we demonstrate physical neural networks with three diverse physical systems-optical, mechanical, and electrical. Physical neural networks may facilitate unconventional machine learning hardware that is orders of magnitude faster and more energy efficient than conventional electronic processors.