Training of Physical Neural Networks

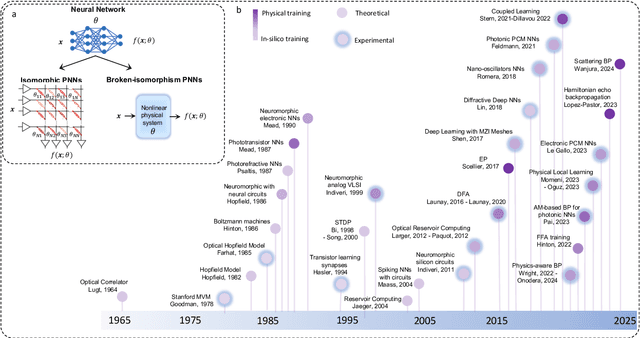
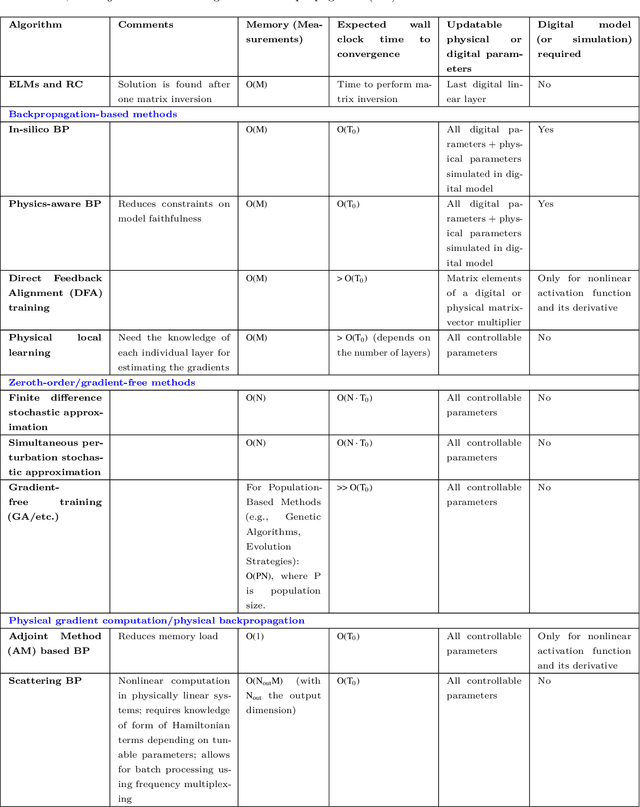
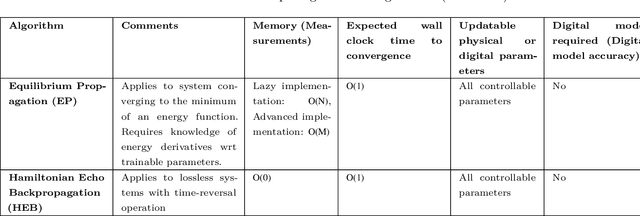
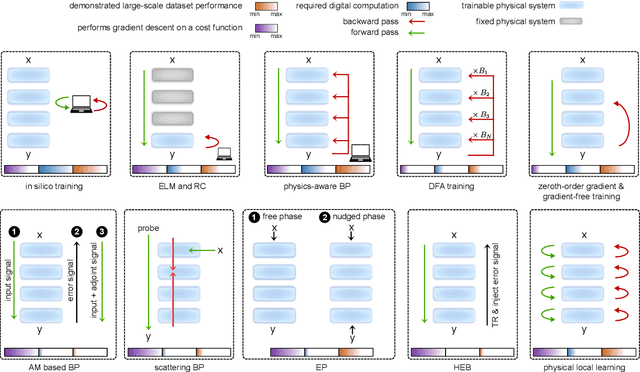
Physical neural networks (PNNs) are a class of neural-like networks that leverage the properties of physical systems to perform computation. While PNNs are so far a niche research area with small-scale laboratory demonstrations, they are arguably one of the most underappreciated important opportunities in modern AI. Could we train AI models 1000x larger than current ones? Could we do this and also have them perform inference locally and privately on edge devices, such as smartphones or sensors? Research over the past few years has shown that the answer to all these questions is likely "yes, with enough research": PNNs could one day radically change what is possible and practical for AI systems. To do this will however require rethinking both how AI models work, and how they are trained - primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs at large scale, many methods including backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs, and so far no method has been shown to scale to the same scale and performance as the backpropagation algorithm widely used in deep learning today. However, this is rapidly changing, and a diverse ecosystem of training techniques provides clues for how PNNs may one day be utilized to create both more efficient realizations of current-scale AI models, and to enable unprecedented-scale models.

Efficient Computation Using Spatial-Photonic Ising Machines: Utilizing Low-Rank and Circulant Matrix Constraints

We explore the potential of spatial-photonic Ising machines (SPIMs) to address computationally intensive Ising problems that employ low-rank and circulant coupling matrices. Our results indicate that the performance of SPIMs is critically affected by the rank and precision of the coupling matrices. By developing and assessing advanced decomposition techniques, we expand the range of problems SPIMs can solve, overcoming the limitations of traditional Mattis-type matrices. Our approach accommodates a diverse array of coupling matrices, including those with inherently low ranks, applicable to complex NP-complete problems. We explore the practical benefits of low-rank approximation in optimization tasks, particularly in financial optimization, to demonstrate the real-world applications of SPIMs. Finally, we evaluate the computational limitations imposed by SPIM hardware precision and suggest strategies to optimize the performance of these systems within these constraints.

Large-scale Sustainable Search on Unconventional Computing Hardware

Since the advent of the Internet, quantifying the relative importance of web pages is at the core of search engine methods. According to one algorithm, PageRank, the worldwide web structure is represented by the Google matrix, whose principal eigenvector components assign a numerical value to web pages for their ranking. Finding such a dominant eigenvector on an ever-growing number of web pages becomes a computationally intensive task incompatible with Moore's Law. We demonstrate that special-purpose optical machines such as networks of optical parametric oscillators, lasers, and gain-dissipative condensates, may aid in accelerating the reliable reconstruction of principal eigenvectors of real-life web graphs. We discuss the feasibility of simulating the PageRank algorithm on large Google matrices using such unconventional hardware. We offer alternative rankings based on the minimisation of spin Hamiltonians. Our estimates show that special-purpose optical machines may provide dramatic improvements in power consumption over classical computing architectures.

XY Neural Networks

The classical XY model is a lattice model of statistical mechanics notable for its universality in the rich hierarchy of the optical, laser and condensed matter systems. We show how to build complex structures for machine learning based on the XY model's nonlinear blocks. The final target is to reproduce the deep learning architectures, which can perform complicated tasks usually attributed to such architectures: speech recognition, visual processing, or other complex classification types with high quality. We developed the robust and transparent approach for the construction of such models, which has universal applicability (i.e. does not strongly connect to any particular physical system), allows many possible extensions while at the same time preserving the simplicity of the methodology.