Efficient Computation Using Spatial-Photonic Ising Machines: Utilizing Low-Rank and Circulant Matrix Constraints

We explore the potential of spatial-photonic Ising machines (SPIMs) to address computationally intensive Ising problems that employ low-rank and circulant coupling matrices. Our results indicate that the performance of SPIMs is critically affected by the rank and precision of the coupling matrices. By developing and assessing advanced decomposition techniques, we expand the range of problems SPIMs can solve, overcoming the limitations of traditional Mattis-type matrices. Our approach accommodates a diverse array of coupling matrices, including those with inherently low ranks, applicable to complex NP-complete problems. We explore the practical benefits of low-rank approximation in optimization tasks, particularly in financial optimization, to demonstrate the real-world applications of SPIMs. Finally, we evaluate the computational limitations imposed by SPIM hardware precision and suggest strategies to optimize the performance of these systems within these constraints.

Maximum entropy models capture melodic styles

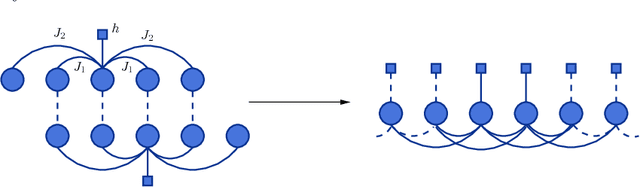
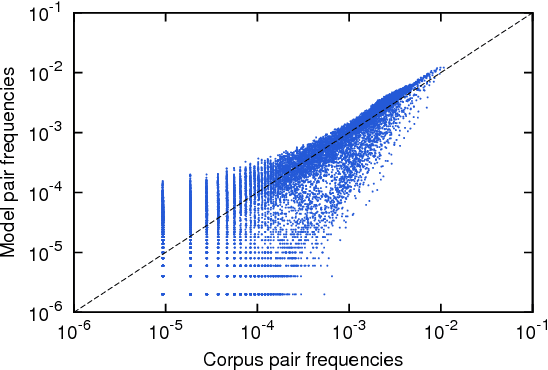
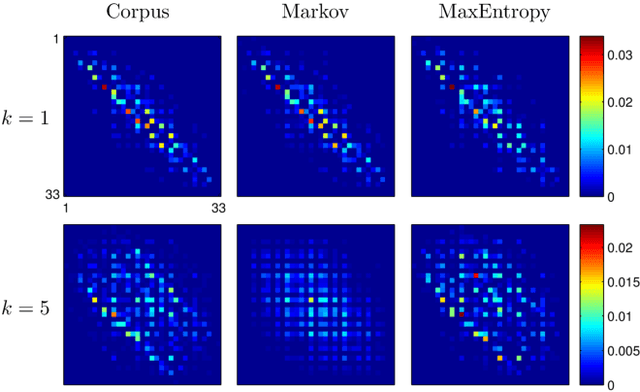
We introduce a Maximum Entropy model able to capture the statistics of melodies in music. The model can be used to generate new melodies that emulate the style of the musical corpus which was used to train it. Instead of using the $n-$body interactions of $(n-1)-$order Markov models, traditionally used in automatic music generation, we use a $k-$nearest neighbour model with pairwise interactions only. In that way, we keep the number of parameters low and avoid over-fitting problems typical of Markov models. We show that long-range musical phrases don't need to be explicitly enforced using high-order Markov interactions, but can instead emerge from multiple, competing, pairwise interactions. We validate our Maximum Entropy model by contrasting how much the generated sequences capture the style of the original corpus without plagiarizing it. To this end we use a data-compression approach to discriminate the levels of borrowing and innovation featured by the artificial sequences. The results show that our modelling scheme outperforms both fixed-order and variable-order Markov models. This shows that, despite being based only on pairwise interactions, this Maximum Entropy scheme opens the possibility to generate musically sensible alterations of the original phrases, providing a way to generate innovation.

Style Imitation and Chord Invention in Polyphonic Music with Exponential Families

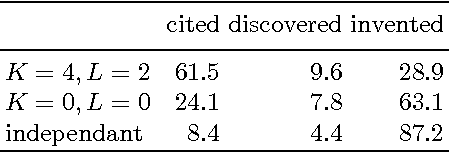
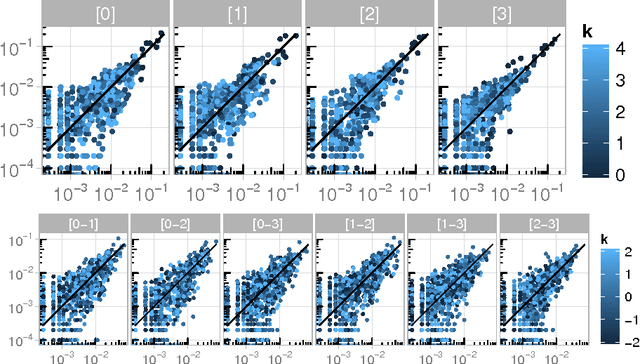
Modeling polyphonic music is a particularly challenging task because of the intricate interplay between melody and harmony. A good model should satisfy three requirements: statistical accuracy (capturing faithfully the statistics of correlations at various ranges, horizontally and vertically), flexibility (coping with arbitrary user constraints), and generalization capacity (inventing new material, while staying in the style of the training corpus). Models proposed so far fail on at least one of these requirements. We propose a statistical model of polyphonic music, based on the maximum entropy principle. This model is able to learn and reproduce pairwise statistics between neighboring note events in a given corpus. The model is also able to invent new chords and to harmonize unknown melodies. We evaluate the invention capacity of the model by assessing the amount of cited, re-discovered, and invented chords on a corpus of Bach chorales. We discuss how the model enables the user to specify and enforce user-defined constraints, which makes it useful for style-based, interactive music generation.