Zero-shot Musical Stem Retrieval with Joint-Embedding Predictive Architectures

In this paper, we tackle the task of musical stem retrieval. Given a musical mix, it consists in retrieving a stem that would fit with it, i.e., that would sound pleasant if played together. To do so, we introduce a new method based on Joint-Embedding Predictive Architectures, where an encoder and a predictor are jointly trained to produce latent representations of a context and predict latent representations of a target. In particular, we design our predictor to be conditioned on arbitrary instruments, enabling our model to perform zero-shot stem retrieval. In addition, we discover that pretraining the encoder using contrastive learning drastically improves the model's performance. We validate the retrieval performances of our model using the MUSDB18 and MoisesDB datasets. We show that it significantly outperforms previous baselines on both datasets, showcasing its ability to support more or less precise (and possibly unseen) conditioning. We also evaluate the learned embeddings on a beat tracking task, demonstrating that they retain temporal structure and local information.

Stem-JEPA: A Joint-Embedding Predictive Architecture for Musical Stem Compatibility Estimation

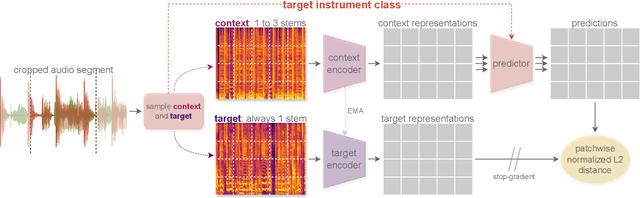
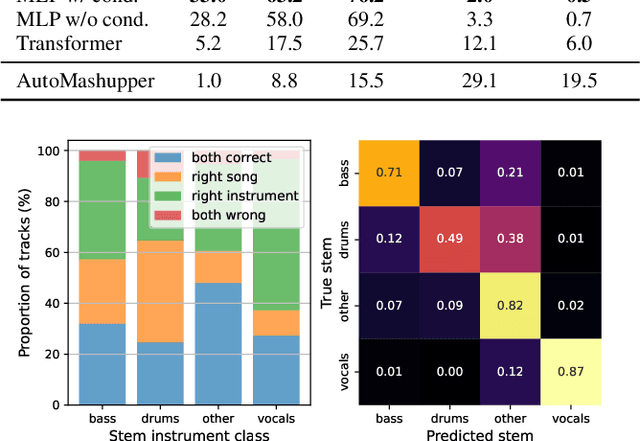
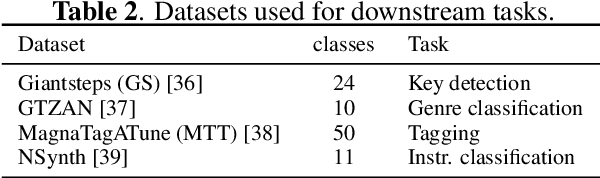
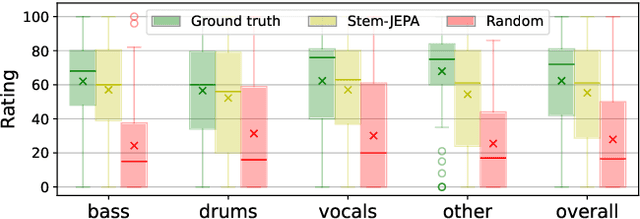
This paper explores the automated process of determining stem compatibility by identifying audio recordings of single instruments that blend well with a given musical context. To tackle this challenge, we present Stem-JEPA, a novel Joint-Embedding Predictive Architecture (JEPA) trained on a multi-track dataset using a self-supervised learning approach. Our model comprises two networks: an encoder and a predictor, which are jointly trained to predict the embeddings of compatible stems from the embeddings of a given context, typically a mix of several instruments. Training a model in this manner allows its use in estimating stem compatibility - retrieving, aligning, or generating a stem to match a given mix - or for downstream tasks such as genre or key estimation, as the training paradigm requires the model to learn information related to timbre, harmony, and rhythm. We evaluate our model's performance on a retrieval task on the MUSDB18 dataset, testing its ability to find the missing stem from a mix and through a subjective user study. We also show that the learned embeddings capture temporal alignment information and, finally, evaluate the representations learned by our model on several downstream tasks, highlighting that they effectively capture meaningful musical features.

Investigating Design Choices in Joint-Embedding Predictive Architectures for General Audio Representation Learning

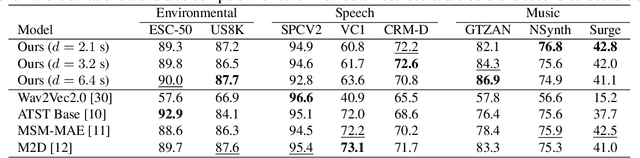
This paper addresses the problem of self-supervised general-purpose audio representation learning. We explore the use of Joint-Embedding Predictive Architectures (JEPA) for this task, which consists of splitting an input mel-spectrogram into two parts (context and target), computing neural representations for each, and training the neural network to predict the target representations from the context representations. We investigate several design choices within this framework and study their influence through extensive experiments by evaluating our models on various audio classification benchmarks, including environmental sounds, speech and music downstream tasks. We focus notably on which part of the input data is used as context or target and show experimentally that it significantly impacts the model's quality. In particular, we notice that some effective design choices in the image domain lead to poor performance on audio, thus highlighting major differences between these two modalities.

PESTO: Pitch Estimation with Self-supervised Transposition-equivariant Objective

In this paper, we address the problem of pitch estimation using Self Supervised Learning (SSL). The SSL paradigm we use is equivariance to pitch transposition, which enables our model to accurately perform pitch estimation on monophonic audio after being trained only on a small unlabeled dataset. We use a lightweight ($<$ 30k parameters) Siamese neural network that takes as inputs two different pitch-shifted versions of the same audio represented by its Constant-Q Transform. To prevent the model from collapsing in an encoder-only setting, we propose a novel class-based transposition-equivariant objective which captures pitch information. Furthermore, we design the architecture of our network to be transposition-preserving by introducing learnable Toeplitz matrices. We evaluate our model for the two tasks of singing voice and musical instrument pitch estimation and show that our model is able to generalize across tasks and datasets while being lightweight, hence remaining compatible with low-resource devices and suitable for real-time applications. In particular, our results surpass self-supervised baselines and narrow the performance gap between self-supervised and supervised methods for pitch estimation.

The Piano Inpainting Application

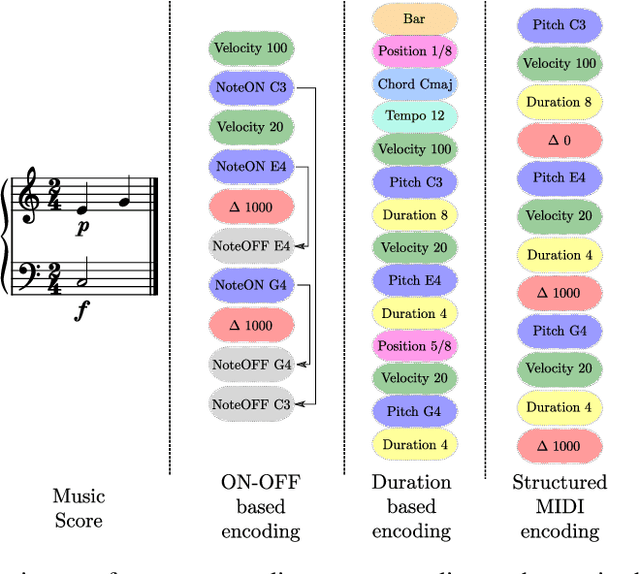
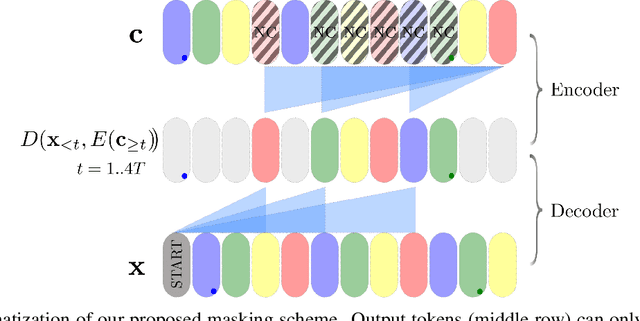
Autoregressive models are now capable of generating high-quality minute-long expressive MIDI piano performances. Even though this progress suggests new tools to assist music composition, we observe that generative algorithms are still not widely used by artists due to the limited control they offer, prohibitive inference times or the lack of integration within musicians' workflows. In this work, we present the Piano Inpainting Application (PIA), a generative model focused on inpainting piano performances, as we believe that this elementary operation (restoring missing parts of a piano performance) encourages human-machine interaction and opens up new ways to approach music composition. Our approach relies on an encoder-decoder Linear Transformer architecture trained on a novel representation for MIDI piano performances termed Structured MIDI Encoding. By uncovering an interesting synergy between Linear Transformers and our inpainting task, we are able to efficiently inpaint contiguous regions of a piano performance, which makes our model suitable for interactive and responsive A.I.-assisted composition. Finally, we introduce our freely-available Ableton Live PIA plugin, which allows musicians to smoothly generate or modify any MIDI clip using PIA within a widely-used professional Digital Audio Workstation.

CRASH: Raw Audio Score-based Generative Modeling for Controllable High-resolution Drum Sound Synthesis

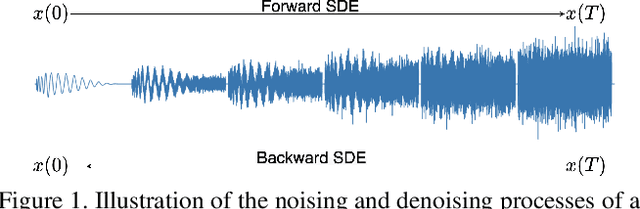
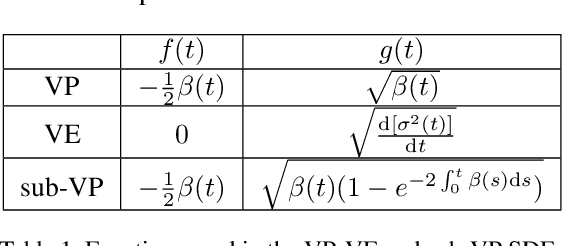
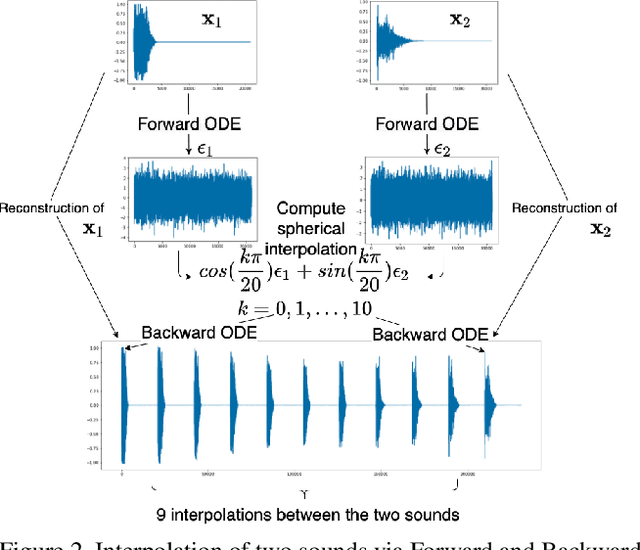
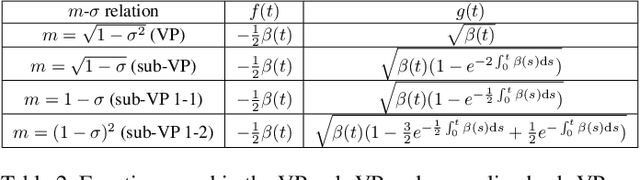
In this paper, we propose a novel score-base generative model for unconditional raw audio synthesis. Our proposal builds upon the latest developments on diffusion process modeling with stochastic differential equations, which already demonstrated promising results on image generation. We motivate novel heuristics for the choice of the diffusion processes better suited for audio generation, and consider the use of a conditional U-Net to approximate the score function. While previous approaches on diffusion models on audio were mainly designed as speech vocoders in medium resolution, our method termed CRASH (Controllable Raw Audio Synthesis with High-resolution) allows us to generate short percussive sounds in 44.1kHz in a controllable way. Through extensive experiments, we showcase on a drum sound generation task the numerous sampling schemes offered by our method (unconditional generation, deterministic generation, inpainting, interpolation, variations, class-conditional sampling) and propose the class-mixing sampling, a novel way to generate "hybrid" sounds. Our proposed method closes the gap with GAN-based methods on raw audio, while offering more flexible generation capabilities with lighter and easier-to-train models.

Spectrogram Inpainting for Interactive Generation of Instrument Sounds

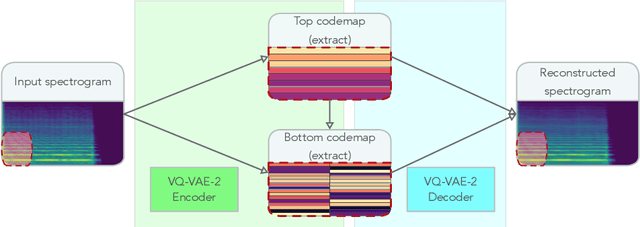
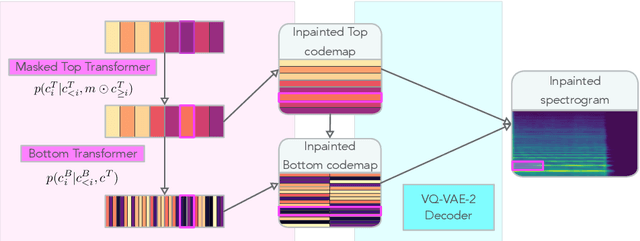
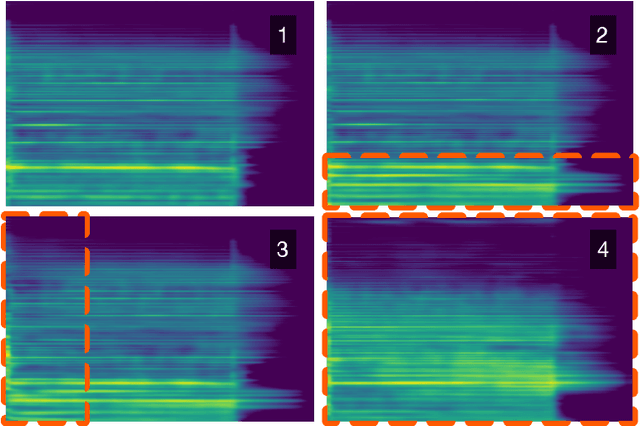
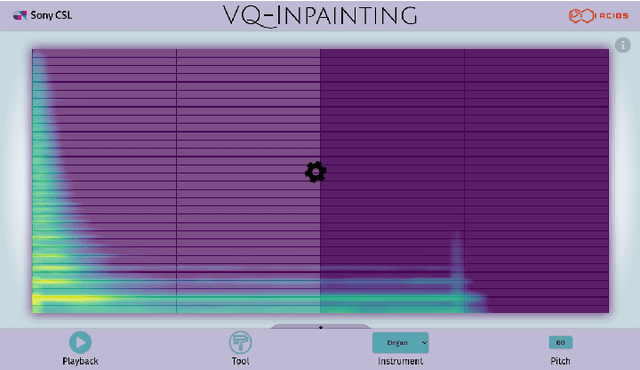
Modern approaches to sound synthesis using deep neural networks are hard to control, especially when fine-grained conditioning information is not available, hindering their adoption by musicians. In this paper, we cast the generation of individual instrumental notes as an inpainting-based task, introducing novel and unique ways to iteratively shape sounds. To this end, we propose a two-step approach: first, we adapt the VQ-VAE-2 image generation architecture to spectrograms in order to convert real-valued spectrograms into compact discrete codemaps, we then implement token-masked Transformers for the inpainting-based generation of these codemaps. We apply the proposed architecture on the NSynth dataset on masked resampling tasks. Most crucially, we open-source an interactive web interface to transform sounds by inpainting, for artists and practitioners alike, opening up to new, creative uses.

Incorporating Music Knowledge in Continual Dataset Augmentation for Music Generation

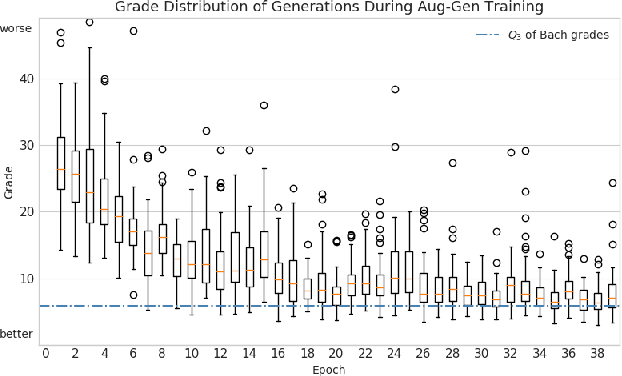
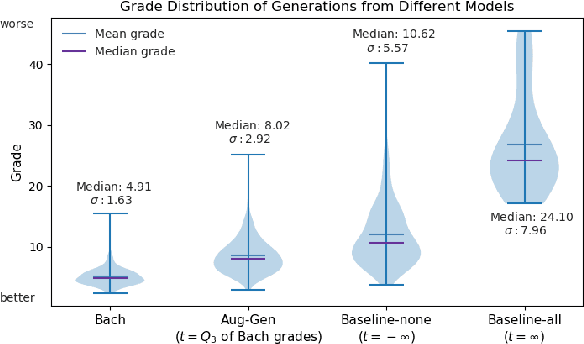
Deep learning has rapidly become the state-of-the-art approach for music generation. However, training a deep model typically requires a large training set, which is often not available for specific musical styles. In this paper, we present augmentative generation (Aug-Gen), a method of dataset augmentation for any music generation system trained on a resource-constrained domain. The key intuition of this method is that the training data for a generative system can be augmented by examples the system produces during the course of training, provided these examples are of sufficiently high quality and variety. We apply Aug-Gen to Transformer-based chorale generation in the style of J.S. Bach, and show that this allows for longer training and results in better generative output.

Vector Quantized Contrastive Predictive Coding for Template-based Music Generation

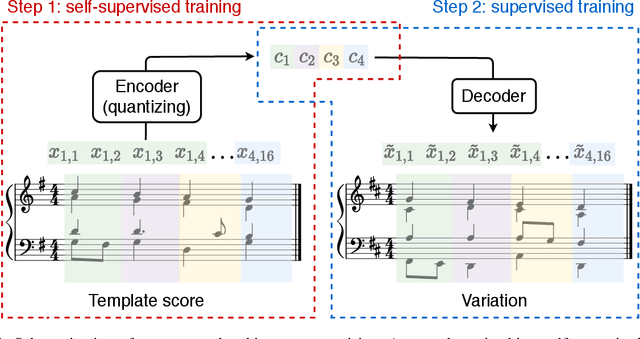
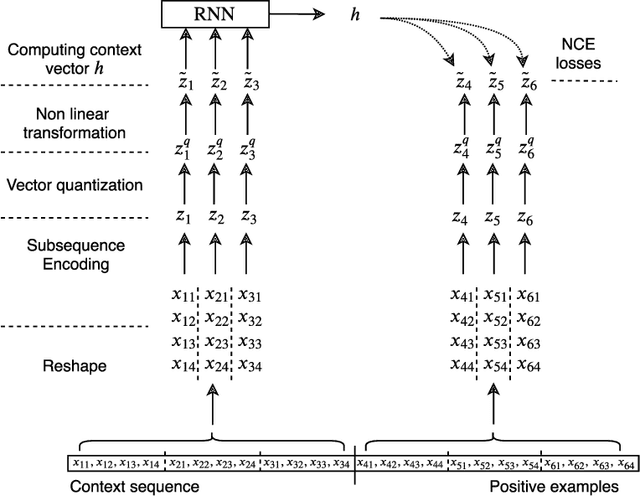
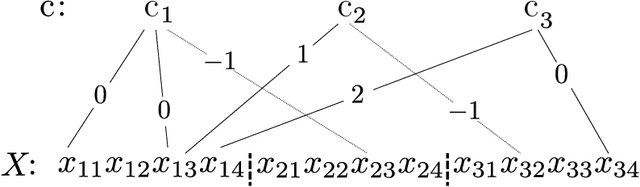
In this work, we propose a flexible method for generating variations of discrete sequences in which tokens can be grouped into basic units, like sentences in a text or bars in music. More precisely, given a template sequence, we aim at producing novel sequences sharing perceptible similarities with the original template without relying on any annotation; so our problem of generating variations is intimately linked to the problem of learning relevant high-level representations without supervision. Our contribution is two-fold: First, we propose a self-supervised encoding technique, named Vector Quantized Contrastive Predictive Coding which allows to learn a meaningful assignment of the basic units over a discrete set of codes, together with mechanisms allowing to control the information content of these learnt discrete representations. Secondly, we show how these compressed representations can be used to generate variations of a template sequence by using an appropriate attention pattern in the Transformer architecture. We illustrate our approach on the corpus of J.S. Bach chorales where we discuss the musical meaning of the learnt discrete codes and show that our proposed method allows to generate coherent and high-quality variations of a given template.

Schoenberg-Rao distances: Entropy-based and geometry-aware statistical Hilbert distances

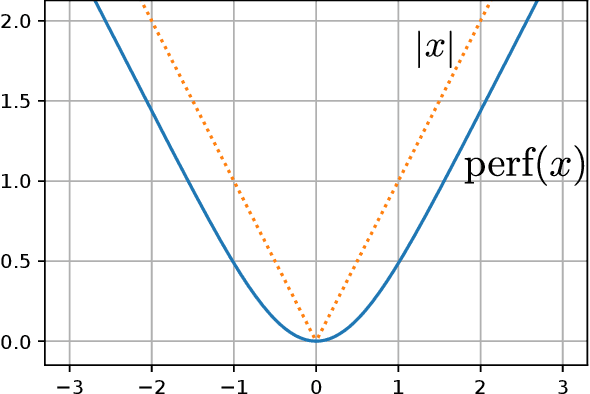
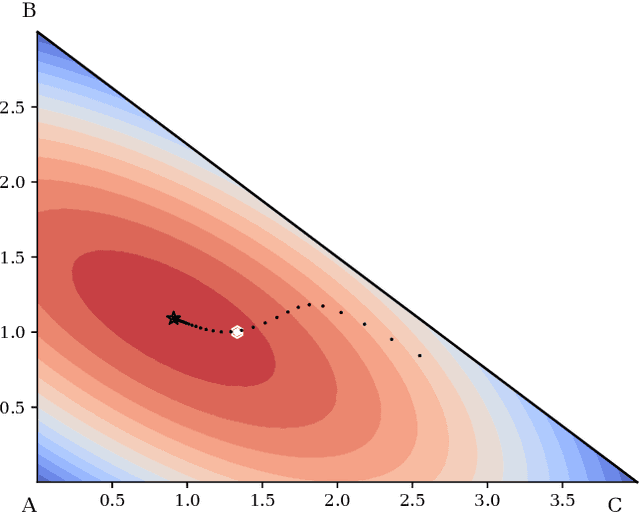
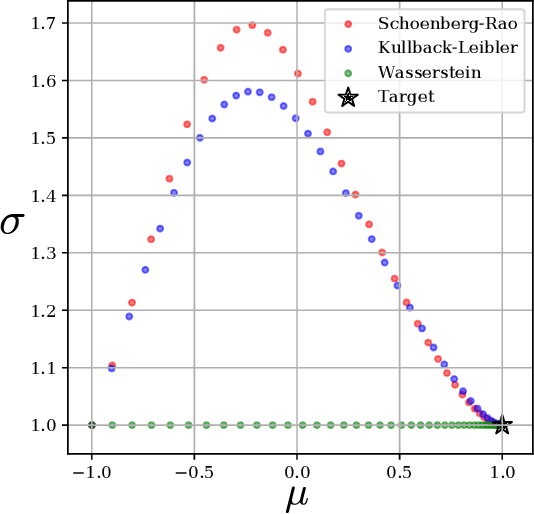
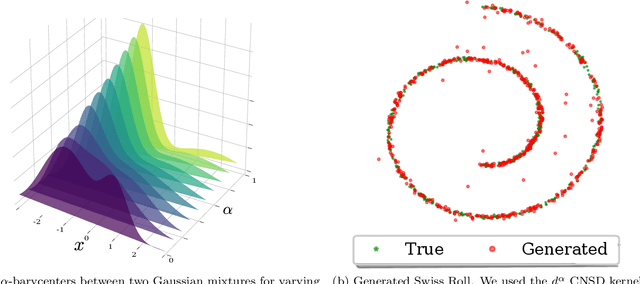
Distances between probability distributions that take into account the geometry of their sample space,like the Wasserstein or the Maximum Mean Discrepancy (MMD) distances have received a lot of attention in machine learning as they can, for instance, be used to compare probability distributions with disjoint supports. In this paper, we study a class of statistical Hilbert distances that we term the Schoenberg-Rao distances, a generalization of the MMD that allows one to consider a broader class of kernels, namely the conditionally negative semi-definite kernels. In particular, we introduce a principled way to construct such kernels and derive novel closed-form distances between mixtures of Gaussian distributions, among others. These distances, derived from the concave Rao's quadratic entropy, enjoy nice theoretical properties and possess interpretable hyperparameters which can be tuned for specific applications. Our method constitutes a practical alternative to Wasserstein distances and we illustrate its efficiency on a broad range of machine learning tasks such as density estimation, generative modeling and mixture simplification.