Meta-learning characteristics and dynamics of quantum systems

While machine learning holds great promise for quantum technologies, most current methods focus on predicting or controlling a specific quantum system. Meta-learning approaches, however, can adapt to new systems for which little data is available, by leveraging knowledge obtained from previous data associated with similar systems. In this paper, we meta-learn dynamics and characteristics of closed and open two-level systems, as well as the Heisenberg model. Based on experimental data of a Loss-DiVincenzo spin-qubit hosted in a Ge/Si core/shell nanowire for different gate voltage configurations, we predict qubit characteristics i.e. $g$-factor and Rabi frequency using meta-learning. The algorithm we introduce improves upon previous state-of-the-art meta-learning methods for physics-based systems by introducing novel techniques such as adaptive learning rates and a global optimizer for improved robustness and increased computational efficiency. We benchmark our method against other meta-learning methods, a vanilla transformer, and a multilayer perceptron, and demonstrate improved performance.

Quantum feedback control with a transformer neural network architecture

Attention-based neural networks such as transformers have revolutionized various fields such as natural language processing, genomics, and vision. Here, we demonstrate the use of transformers for quantum feedback control through a supervised learning approach. In particular, due to the transformer's ability to capture long-range temporal correlations and training efficiency, we show that it can surpass some of the limitations of previous control approaches, e.g.~those based on recurrent neural networks trained using a similar approach or reinforcement learning. We numerically show, for the example of state stabilization of a two-level system, that our bespoke transformer architecture can achieve unit fidelity to a target state in a short time even in the presence of inefficient measurement and Hamiltonian perturbations that were not included in the training set. We also demonstrate that this approach generalizes well to the control of non-Markovian systems. Our approach can be used for quantum error correction, fast control of quantum states in the presence of colored noise, as well as real-time tuning, and characterization of quantum devices.

Quantum Equilibrium Propagation for efficient training of quantum systems based on Onsager reciprocity

The widespread adoption of machine learning and artificial intelligence in all branches of science and technology has created a need for energy-efficient, alternative hardware platforms. While such neuromorphic approaches have been proposed and realised for a wide range of platforms, physically extracting the gradients required for training remains challenging as generic approaches only exist in certain cases. Equilibrium propagation (EP) is such a procedure that has been introduced and applied to classical energy-based models which relax to an equilibrium. Here, we show a direct connection between EP and Onsager reciprocity and exploit this to derive a quantum version of EP. This can be used to optimize loss functions that depend on the expectation values of observables of an arbitrary quantum system. Specifically, we illustrate this new concept with supervised and unsupervised learning examples in which the input or the solvable task is of quantum mechanical nature, e.g., the recognition of quantum many-body ground states, quantum phase exploration, sensing and phase boundary exploration. We propose that in the future quantum EP may be used to solve tasks such as quantum phase discovery with a quantum simulator even for Hamiltonians which are numerically hard to simulate or even partially unknown. Our scheme is relevant for a variety of quantum simulation platforms such as ion chains, superconducting qubit arrays, neutral atom Rydberg tweezer arrays and strongly interacting atoms in optical lattices.

Training of Physical Neural Networks

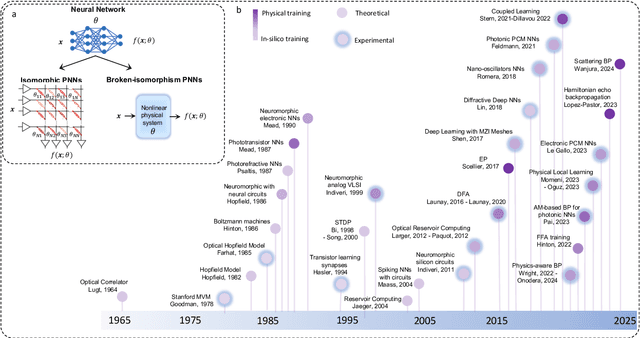
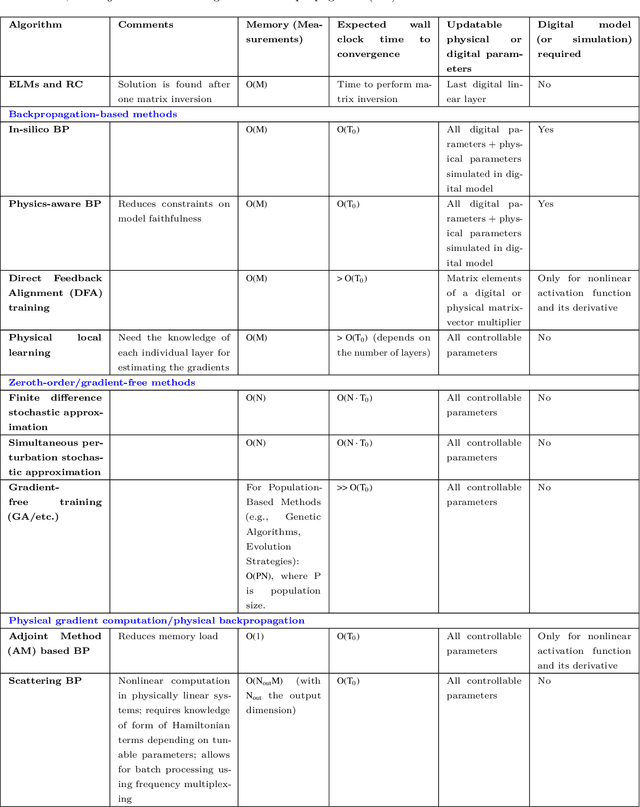
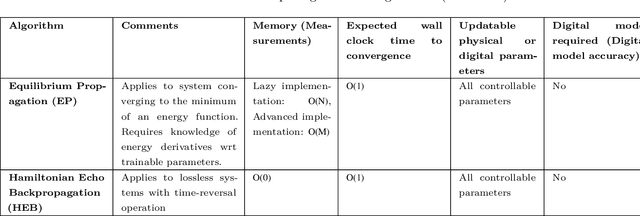
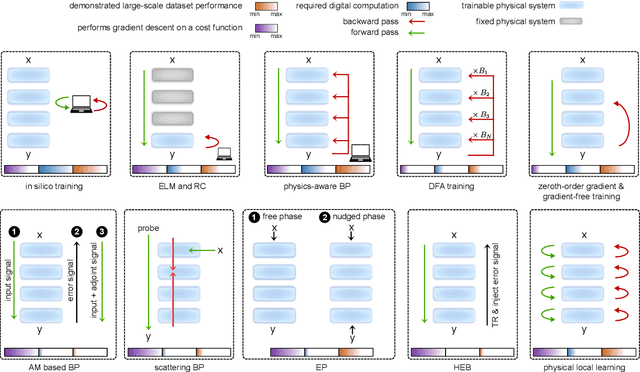
Physical neural networks (PNNs) are a class of neural-like networks that leverage the properties of physical systems to perform computation. While PNNs are so far a niche research area with small-scale laboratory demonstrations, they are arguably one of the most underappreciated important opportunities in modern AI. Could we train AI models 1000x larger than current ones? Could we do this and also have them perform inference locally and privately on edge devices, such as smartphones or sensors? Research over the past few years has shown that the answer to all these questions is likely "yes, with enough research": PNNs could one day radically change what is possible and practical for AI systems. To do this will however require rethinking both how AI models work, and how they are trained - primarily by considering the problems through the constraints of the underlying hardware physics. To train PNNs at large scale, many methods including backpropagation-based and backpropagation-free approaches are now being explored. These methods have various trade-offs, and so far no method has been shown to scale to the same scale and performance as the backpropagation algorithm widely used in deep learning today. However, this is rapidly changing, and a diverse ecosystem of training techniques provides clues for how PNNs may one day be utilized to create both more efficient realizations of current-scale AI models, and to enable unprecedented-scale models.

Tackling Decision Processes with Non-Cumulative Objectives using Reinforcement Learning

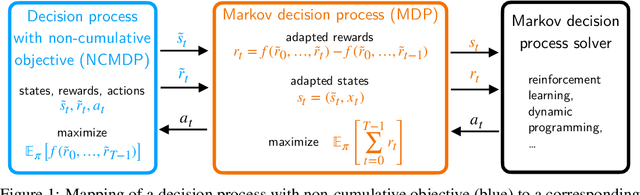
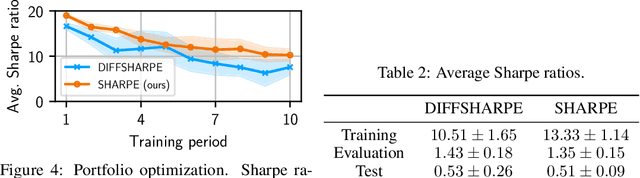
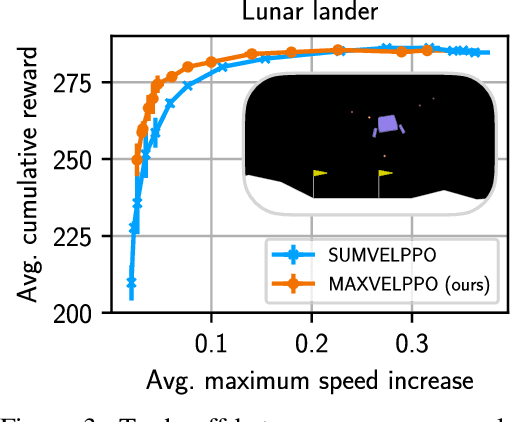
Markov decision processes (MDPs) are used to model a wide variety of applications ranging from game playing over robotics to finance. Their optimal policy typically maximizes the expected sum of rewards given at each step of the decision process. However, a large class of problems does not fit straightforwardly into this framework: Non-cumulative Markov decision processes (NCMDPs), where instead of the expected sum of rewards, the expected value of an arbitrary function of the rewards is maximized. Example functions include the maximum of the rewards or their mean divided by their standard deviation. In this work, we introduce a general mapping of NCMDPs to standard MDPs. This allows all techniques developed to find optimal policies for MDPs, such as reinforcement learning or dynamic programming, to be directly applied to the larger class of NCMDPs. Focusing on reinforcement learning, we show applications in a diverse set of tasks, including classical control, portfolio optimization in finance, and discrete optimization problems. Given our approach, we can improve both final performance and training time compared to relying on standard MDPs.

Training Coupled Phase Oscillators as a Neuromorphic Platform using Equilibrium Propagation

Given the rapidly growing scale and resource requirements of machine learning applications, the idea of building more efficient learning machines much closer to the laws of physics is an attractive proposition. One central question for identifying promising candidates for such neuromorphic platforms is whether not only inference but also training can exploit the physical dynamics. In this work, we show that it is possible to successfully train a system of coupled phase oscillators - one of the most widely investigated nonlinear dynamical systems with a multitude of physical implementations, comprising laser arrays, coupled mechanical limit cycles, superfluids, and exciton-polaritons. To this end, we apply the approach of equilibrium propagation, which permits to extract training gradients via a physical realization of backpropagation, based only on local interactions. The complex energy landscape of the XY/ Kuramoto model leads to multistability, and we show how to address this challenge. Our study identifies coupled phase oscillators as a new general-purpose neuromorphic platform and opens the door towards future experimental implementations.

Optimizing ZX-Diagrams with Deep Reinforcement Learning

ZX-diagrams are a powerful graphical language for the description of quantum processes with applications in fundamental quantum mechanics, quantum circuit optimization, tensor network simulation, and many more. The utility of ZX-diagrams relies on a set of local transformation rules that can be applied to them without changing the underlying quantum process they describe. These rules can be exploited to optimize the structure of ZX-diagrams for a range of applications. However, finding an optimal sequence of transformation rules is generally an open problem. In this work, we bring together ZX-diagrams with reinforcement learning, a machine learning technique designed to discover an optimal sequence of actions in a decision-making problem and show that a trained reinforcement learning agent can significantly outperform other optimization techniques like a greedy strategy or simulated annealing. The use of graph neural networks to encode the policy of the agent enables generalization to diagrams much bigger than seen during the training phase.

Deep Bayesian Experimental Design for Quantum Many-Body Systems

Bayesian experimental design is a technique that allows to efficiently select measurements to characterize a physical system by maximizing the expected information gain. Recent developments in deep neural networks and normalizing flows allow for a more efficient approximation of the posterior and thus the extension of this technique to complex high-dimensional situations. In this paper, we show how this approach holds promise for adaptive measurement strategies to characterize present-day quantum technology platforms. In particular, we focus on arrays of coupled cavities and qubit arrays. Both represent model systems of high relevance for modern applications, like quantum simulations and computing, and both have been realized in platforms where measurement and control can be exploited to characterize and counteract unavoidable disorder. Thus, they represent ideal targets for applications of Bayesian experimental design.

Investigation of inverse design of multilayer thin-films with conditional invertible Neural Networks

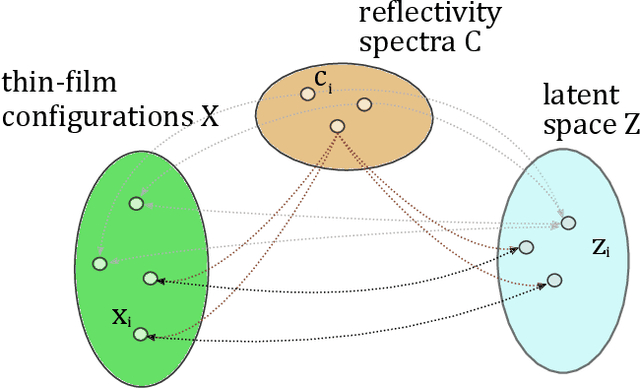
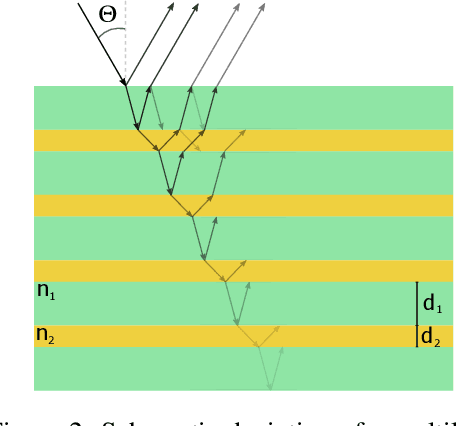
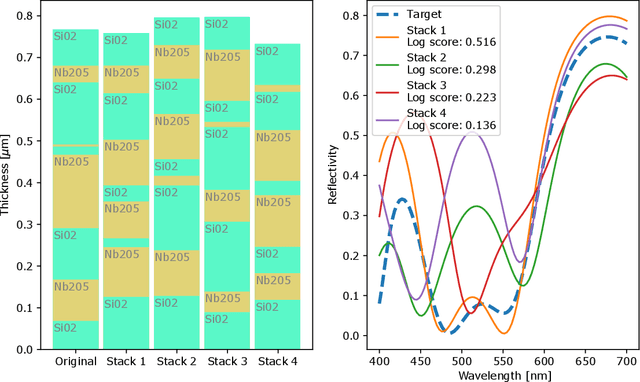
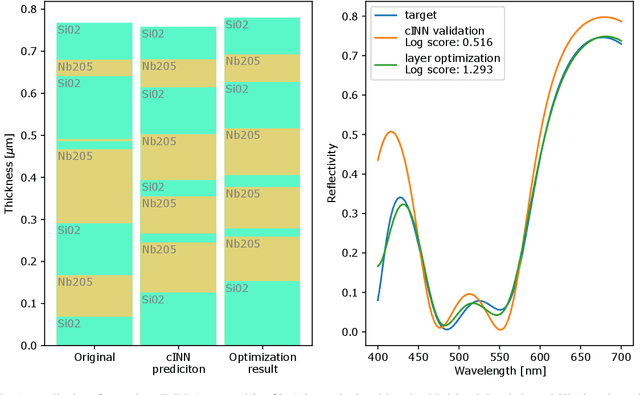
The task of designing optical multilayer thin-films regarding a given target is currently solved using gradient-based optimization in conjunction with methods that can introduce additional thin-film layers. Recently, Deep Learning and Reinforcement Learning have been been introduced to the task of designing thin-films with great success, however a trained network is usually only able to become proficient for a single target and must be retrained if the optical targets are varied. In this work, we apply conditional Invertible Neural Networks (cINN) to inversely designing multilayer thin-films given an optical target. Since the cINN learns the energy landscape of all thin-film configurations within the training dataset, we show that cINNs can generate a stochastic ensemble of proposals for thin-film configurations that that are reasonably close to the desired target depending only on random variables. By refining the proposed configurations further by a local optimization, we show that the generated thin-films reach the target with significantly greater precision than comparable state-of-the art approaches. Furthermore, we tested the generative capabilities on samples which are outside the training data distribution and found that the cINN was able to predict thin-films for out-of-distribution targets, too. The results suggest that in order to improve the generative design of thin-films, it is instructive to use established and new machine learning methods in conjunction in order to obtain the most favorable results.

Artificial Intelligence and Machine Learning for Quantum Technologies

In recent years, the dramatic progress in machine learning has begun to impact many areas of science and technology significantly. In the present perspective article, we explore how quantum technologies are benefiting from this revolution. We showcase in illustrative examples how scientists in the past few years have started to use machine learning and more broadly methods of artificial intelligence to analyze quantum measurements, estimate the parameters of quantum devices, discover new quantum experimental setups, protocols, and feedback strategies, and generally improve aspects of quantum computing, quantum communication, and quantum simulation. We highlight open challenges and future possibilities and conclude with some speculative visions for the next decade.