Tackling Decision Processes with Non-Cumulative Objectives using Reinforcement Learning
Paper and Code
May 22, 2024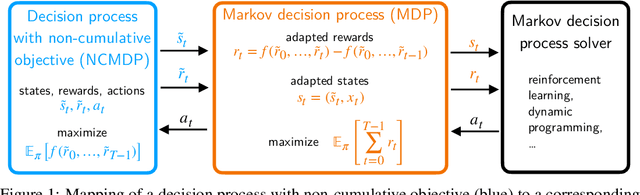

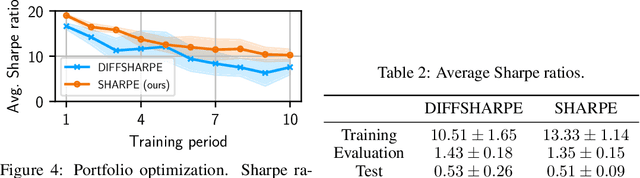
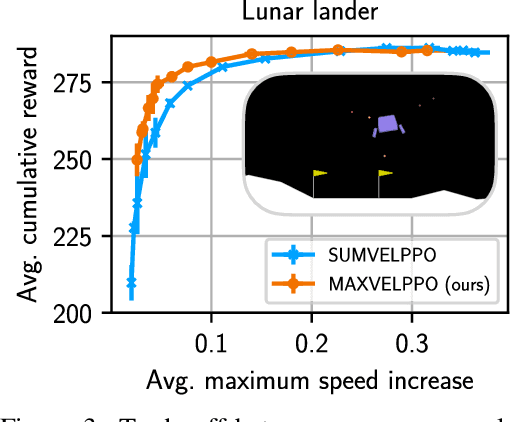
Markov decision processes (MDPs) are used to model a wide variety of applications ranging from game playing over robotics to finance. Their optimal policy typically maximizes the expected sum of rewards given at each step of the decision process. However, a large class of problems does not fit straightforwardly into this framework: Non-cumulative Markov decision processes (NCMDPs), where instead of the expected sum of rewards, the expected value of an arbitrary function of the rewards is maximized. Example functions include the maximum of the rewards or their mean divided by their standard deviation. In this work, we introduce a general mapping of NCMDPs to standard MDPs. This allows all techniques developed to find optimal policies for MDPs, such as reinforcement learning or dynamic programming, to be directly applied to the larger class of NCMDPs. Focusing on reinforcement learning, we show applications in a diverse set of tasks, including classical control, portfolio optimization in finance, and discrete optimization problems. Given our approach, we can improve both final performance and training time compared to relying on standard MDPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge