QuantGraph: A Receding-Horizon Quantum Graph Solver

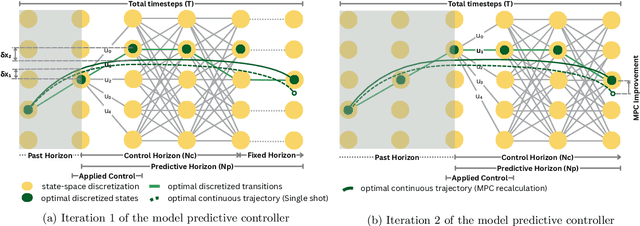
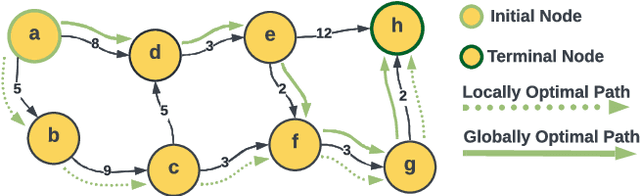
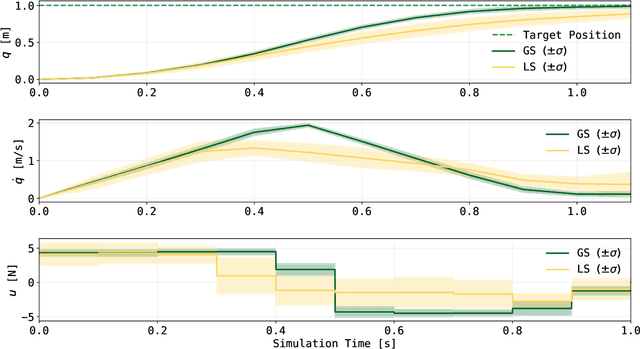
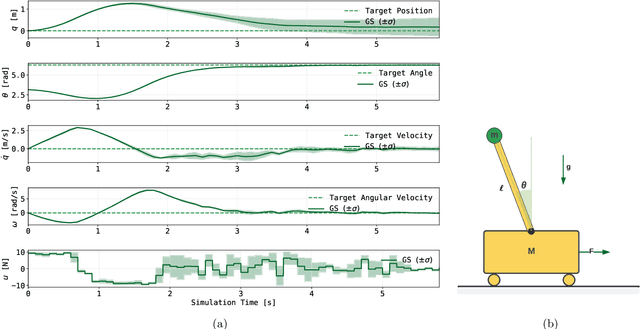
Dynamic programming is a cornerstone of graph-based optimization. While effective, it scales unfavorably with problem size. In this work, we present QuantGraph, a two-stage quantum-enhanced framework that casts local and global graph-optimization problems as quantum searches over discrete trajectory spaces. The solver is designed to operate efficiently by first finding a sequence of locally optimal transitions in the graph (local stage), without considering full trajectories. The accumulated cost of these transitions acts as a threshold that prunes the search space (up to 60% reduction for certain examples). The subsequent global stage, based on this threshold, refines the solution. Both stages utilize variants of the Grover-adaptive-search algorithm. To achieve scalability and robustness, we draw on principles from control theory and embed QuantGraph's global stage within a receding-horizon model-predictive-control scheme. This classical layer stabilizes and guides the quantum search, improving precision and reducing computational burden. In practice, the resulting closed-loop system exhibits robust behavior and lower overall complexity. Notably, for a fixed query budget, QuantGraph attains a 2x increase in control-discretization precision while still benefiting from Grover-search's inherent quadratic speedup compared to classical methods.

MetaSym: A Symplectic Meta-learning Framework for Physical Intelligence

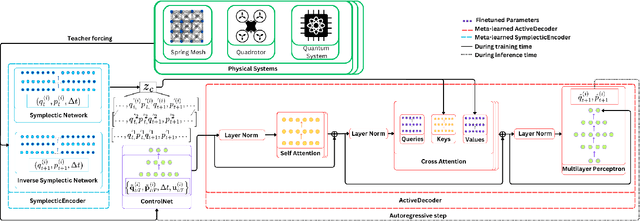
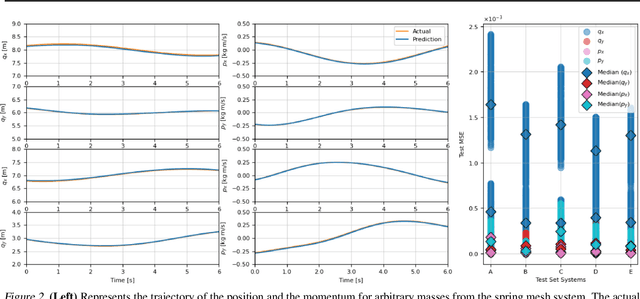
Scalable and generalizable physics-aware deep learning has long been considered a significant challenge with various applications across diverse domains ranging from robotics to molecular dynamics. Central to almost all physical systems are symplectic forms, the geometric backbone that underpins fundamental invariants like energy and momentum. In this work, we introduce a novel deep learning architecture, MetaSym. In particular, MetaSym combines a strong symplectic inductive bias obtained from a symplectic encoder and an autoregressive decoder with meta-attention. This principled design ensures that core physical invariants remain intact while allowing flexible, data-efficient adaptation to system heterogeneities. We benchmark MetaSym on highly varied datasets such as a high-dimensional spring mesh system (Otness et al., 2021), an open quantum system with dissipation and measurement backaction, and robotics-inspired quadrotor dynamics. Our results demonstrate superior performance in modeling dynamics under few-shot adaptation, outperforming state-of-the-art baselines with far larger models.

Quantum feedback control with a transformer neural network architecture

Attention-based neural networks such as transformers have revolutionized various fields such as natural language processing, genomics, and vision. Here, we demonstrate the use of transformers for quantum feedback control through a supervised learning approach. In particular, due to the transformer's ability to capture long-range temporal correlations and training efficiency, we show that it can surpass some of the limitations of previous control approaches, e.g.~those based on recurrent neural networks trained using a similar approach or reinforcement learning. We numerically show, for the example of state stabilization of a two-level system, that our bespoke transformer architecture can achieve unit fidelity to a target state in a short time even in the presence of inefficient measurement and Hamiltonian perturbations that were not included in the training set. We also demonstrate that this approach generalizes well to the control of non-Markovian systems. Our approach can be used for quantum error correction, fast control of quantum states in the presence of colored noise, as well as real-time tuning, and characterization of quantum devices.