Optical Diffraction Tomography based on 3D Physics-Inspired Neural Network (PINN)
Paper and Code
Jun 10, 2022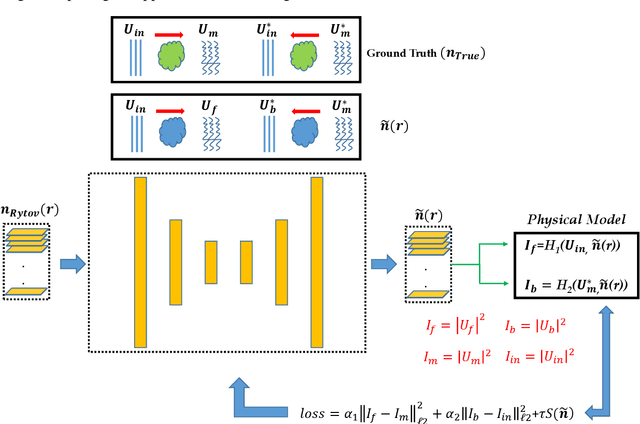

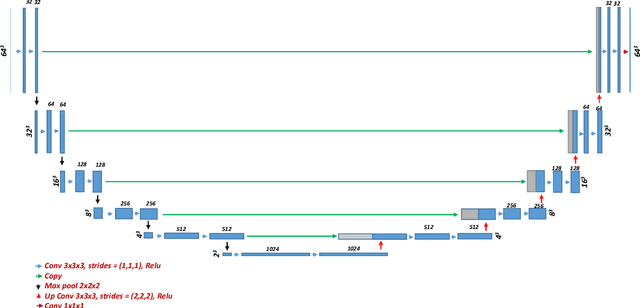

Optical diffraction tomography (ODT) is an emerging 3D imaging technique that is used for the 3D reconstruction of the refractive index (RI) for semi-transparent samples. Various inverse models have been proposed to reconstruct the 3D RI based on the holographic detection of different samples such as the Born and the Rytov approximations. However, such approximations usually suffer from the so-called missing-cone problem that results in an elongation of the final reconstruction along the optical axis. Different iterative schemes have been proposed to solve the missing cone problem relying on physical forward models and an error function that aims at filling in the k-space and thus eliminating the missing-cone problem and reaching better reconstruction accuracy. In this paper, we propose a different approach where a 3D neural network (NN) is employed. The NN is trained with a cost function derived from a physical model based on the physics of optical wave propagation. The 3D NN starts with an initial guess for the 3D RI reconstruction (i.e. Born, or Rytov) and aims at reconstructing better 3D reconstruction based on an error function. With this technique, the NN can be trained without any examples of the relation between the ill-posed reconstruction (Born or Rytov) and the ground truth (true shape).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge