Subwavelength Imaging using a Solid-Immersion Diffractive Optical Processor

Phase imaging is widely used in biomedical imaging, sensing, and material characterization, among other fields. However, direct imaging of phase objects with subwavelength resolution remains a challenge. Here, we demonstrate subwavelength imaging of phase and amplitude objects based on all-optical diffractive encoding and decoding. To resolve subwavelength features of an object, the diffractive imager uses a thin, high-index solid-immersion layer to transmit high-frequency information of the object to a spatially-optimized diffractive encoder, which converts/encodes high-frequency information of the input into low-frequency spatial modes for transmission through air. The subsequent diffractive decoder layers (in air) are jointly designed with the encoder using deep-learning-based optimization, and communicate with the encoder layer to create magnified images of input objects at its output, revealing subwavelength features that would otherwise be washed away due to diffraction limit. We demonstrate that this all-optical collaboration between a diffractive solid-immersion encoder and the following decoder layers in air can resolve subwavelength phase and amplitude features of input objects in a highly compact design. To experimentally demonstrate its proof-of-concept, we used terahertz radiation and developed a fabrication method for creating monolithic multi-layer diffractive processors. Through these monolithically fabricated diffractive encoder-decoder pairs, we demonstrated phase-to-intensity transformations and all-optically reconstructed subwavelength phase features of input objects by directly transforming them into magnified intensity features at the output. This solid-immersion-based diffractive imager, with its compact and cost-effective design, can find wide-ranging applications in bioimaging, endoscopy, sensing and materials characterization.

Physics-informed neural networks for diffraction tomography

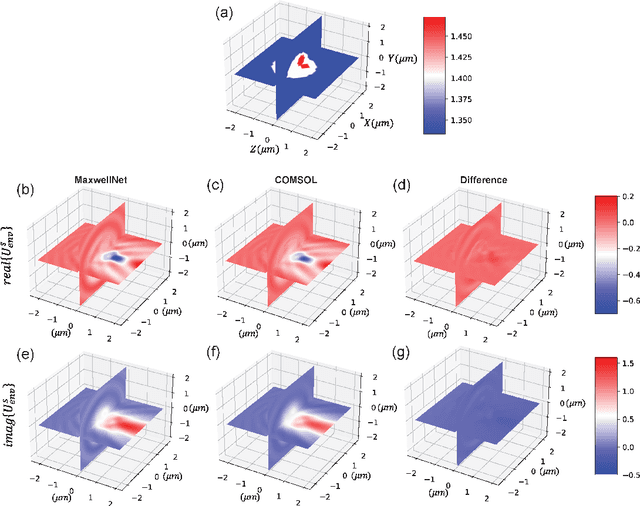
We propose a physics-informed neural network as the forward model for tomographic reconstructions of biological samples. We demonstrate that by training this network with the Helmholtz equation as a physical loss, we can predict the scattered field accurately. It will be shown that a pretrained network can be fine-tuned for different samples and used for solving the scattering problem much faster than other numerical solutions. We evaluate our methodology with numerical and experimental results. Our physics-informed neural networks can be generalized for any forward and inverse scattering problem.

Optical Diffraction Tomography based on 3D Physics-Inspired Neural Network (PINN)

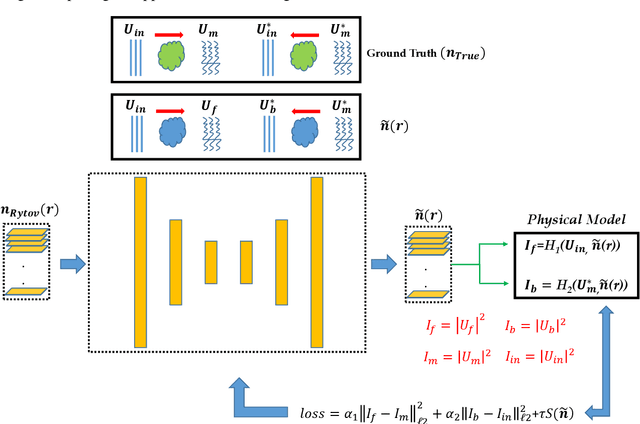
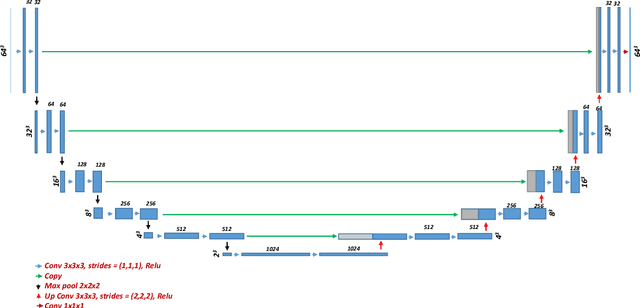
Optical diffraction tomography (ODT) is an emerging 3D imaging technique that is used for the 3D reconstruction of the refractive index (RI) for semi-transparent samples. Various inverse models have been proposed to reconstruct the 3D RI based on the holographic detection of different samples such as the Born and the Rytov approximations. However, such approximations usually suffer from the so-called missing-cone problem that results in an elongation of the final reconstruction along the optical axis. Different iterative schemes have been proposed to solve the missing cone problem relying on physical forward models and an error function that aims at filling in the k-space and thus eliminating the missing-cone problem and reaching better reconstruction accuracy. In this paper, we propose a different approach where a 3D neural network (NN) is employed. The NN is trained with a cost function derived from a physical model based on the physics of optical wave propagation. The 3D NN starts with an initial guess for the 3D RI reconstruction (i.e. Born, or Rytov) and aims at reconstructing better 3D reconstruction based on an error function. With this technique, the NN can be trained without any examples of the relation between the ill-posed reconstruction (Born or Rytov) and the ground truth (true shape).