Learning Coarse-Grained Dynamics on Graph

We consider a Graph Neural Network (GNN) non-Markovian modeling framework to identify coarse-grained dynamical systems on graphs. Our main idea is to systematically determine the GNN architecture by inspecting how the leading term of the Mori-Zwanzig memory term depends on the coarse-grained interaction coefficients that encode the graph topology. Based on this analysis, we found that the appropriate GNN architecture that will account for $K$-hop dynamical interactions has to employ a Message Passing (MP) mechanism with at least $2K$ steps. We also deduce that the memory length required for an accurate closure model decreases as a function of the interaction strength under the assumption that the interaction strength exhibits a power law that decays as a function of the hop distance. Supporting numerical demonstrations on two examples, a heterogeneous Kuramoto oscillator model and a power system, suggest that the proposed GNN architecture can predict the coarse-grained dynamics under fixed and time-varying graph topologies.

Modal Analysis of Spatiotemporal Data via Multivariate Gaussian Process Regression

Modal analysis has become an essential tool to understand the coherent structure of complex flows. The classical modal analysis methods, such as dynamic mode decomposition (DMD) and spectral proper orthogonal decomposition (SPOD), rely on a sufficient amount of data that is regularly sampled in time. However, often one needs to deal with sparse temporally irregular data, e.g., due to experimental measurements and simulation algorithm. To overcome the limitations of data scarcity and irregular sampling, we propose a novel modal analysis technique using multi-variate Gaussian process regression (MVGPR). We first establish the connection between MVGPR and the existing modal analysis techniques, DMD and SPOD, from a linear system identification perspective. Next, leveraging this connection, we develop a MVGPR-based modal analysis technique that addresses the aforementioned limitations. The capability of MVGPR is endowed by its judiciously designed kernel structure for correlation function, that is derived from the assumed linear dynamics. Subsequently, the proposed MVGPR method is benchmarked against DMD and SPOD on a range of examples, from academic and synthesized data to unsteady airfoil aerodynamics. The results demonstrate MVGPR as a promising alternative to classical modal analysis methods, especially in the scenario of scarce and temporally irregular data.

PyPose v0.6: The Imperative Programming Interface for Robotics

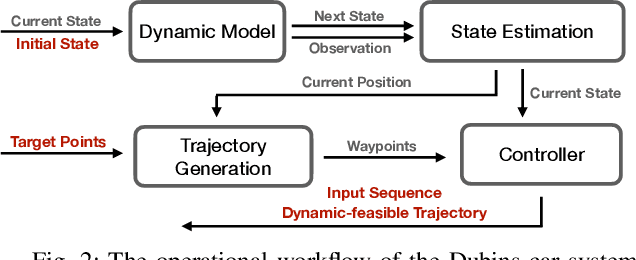
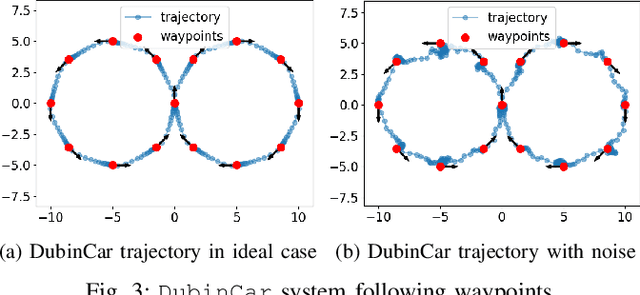
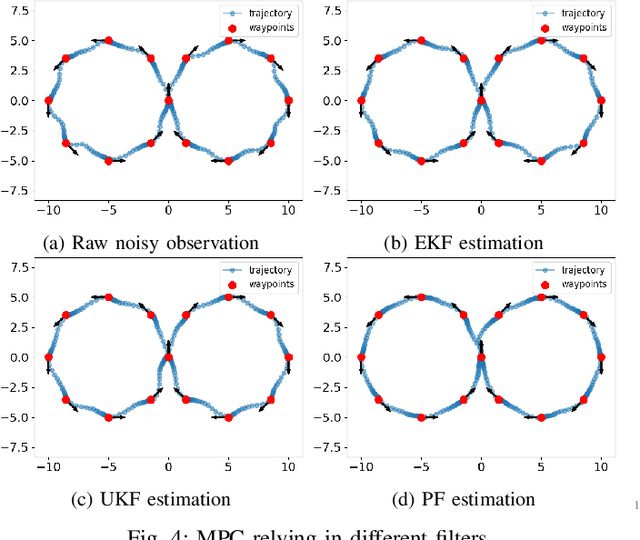
PyPose is an open-source library for robot learning. It combines a learning-based approach with physics-based optimization, which enables seamless end-to-end robot learning. It has been used in many tasks due to its meticulously designed application programming interface (API) and efficient implementation. From its initial launch in early 2022, PyPose has experienced significant enhancements, incorporating a wide variety of new features into its platform. To satisfy the growing demand for understanding and utilizing the library and reduce the learning curve of new users, we present the fundamental design principle of the imperative programming interface, and showcase the flexible usage of diverse functionalities and modules using an extremely simple Dubins car example. We also demonstrate that the PyPose can be easily used to navigate a real quadruped robot with a few lines of code.

Learning Koopman Operators with Control Using Bi-level Optimization

The accurate modeling and control of nonlinear dynamical effects are crucial for numerous robotic systems. The Koopman formalism emerges as a valuable tool for linear control design in nonlinear systems within unknown environments. However, it still remains a challenging task to learn the Koopman operator with control from data, and in particular, the simultaneous identification of the Koopman linear dynamics and the mapping between the state and Koopman spaces. Conventional approaches, based on single-level unconstrained optimization, may lack model robustness, training efficiency, and long-term predictive accuracy. This paper presents a bi-level optimization framework that jointly learns the Koopman embedding mapping and Koopman dynamics with explicit multi-step dynamical constraints, eliminating the need for heuristically-tuned loss terms. Leveraging implicit differentiation, our formulation allows back-propagation in standard learning framework and the use of state-of-the-art optimizers, yielding more stable and robust system performance over various applications compared to conventional methods.

PyPose: A Library for Robot Learning with Physics-based Optimization

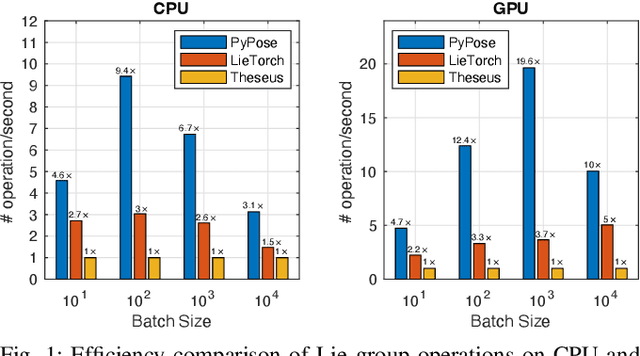
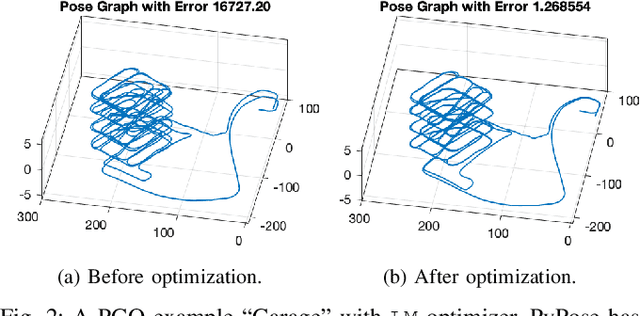
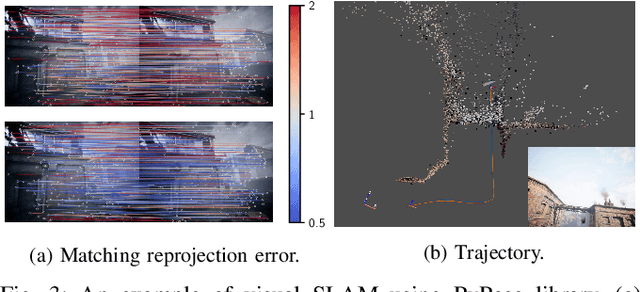
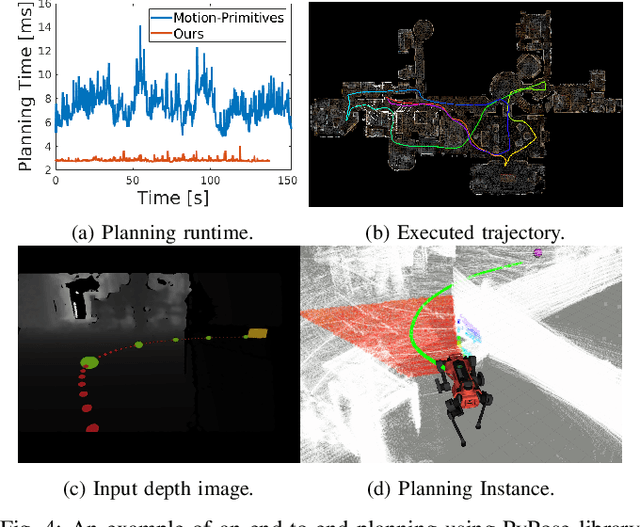
Deep learning has had remarkable success in robotic perception, but its data-centric nature suffers when it comes to generalizing to ever-changing environments. By contrast, physics-based optimization generalizes better, but it does not perform as well in complicated tasks due to the lack of high-level semantic information and the reliance on manual parametric tuning. To take advantage of these two complementary worlds, we present PyPose: a robotics-oriented, PyTorch-based library that combines deep perceptual models with physics-based optimization techniques. Our design goal for PyPose is to make it user-friendly, efficient, and interpretable with a tidy and well-organized architecture. Using an imperative style interface, it can be easily integrated into real-world robotic applications. Besides, it supports parallel computing of any order gradients of Lie groups and Lie algebras and $2^{\text{nd}}$-order optimizers, such as trust region methods. Experiments show that PyPose achieves 3-20$\times$ speedup in computation compared to state-of-the-art libraries. To boost future research, we provide concrete examples across several fields of robotics, including SLAM, inertial navigation, planning, and control.