ATAS: Any-to-Any Self-Distillation for Enhanced Open-Vocabulary Dense Prediction

Vision-language models such as CLIP have recently propelled open-vocabulary dense prediction tasks by enabling recognition of a broad range of visual concepts. However, CLIP still struggles with fine-grained, region-level understanding, hindering its effectiveness on these dense prediction tasks. We identify two pivotal factors required to address this limitation: semantic coherence and fine-grained vision-language alignment. Current adaptation methods often improve fine-grained alignment at the expense of semantic coherence, and often rely on extra modules or supervised fine-tuning. To overcome these issues, we propose Any-to-Any Self-Distillation (ATAS), a novel approach that simultaneously enhances semantic coherence and fine-grained alignment by leveraging own knowledge of a model across all representation levels. Unlike prior methods, ATAS uses only unlabeled images and an internal self-distillation process to refine representations of CLIP vision encoders, preserving local semantic consistency while sharpening local detail recognition. On open-vocabulary object detection and semantic segmentation benchmarks, ATAS achieves substantial performance gains, outperforming baseline CLIP models. These results validate the effectiveness of our approach and underscore the importance of jointly maintaining semantic coherence and fine-grained alignment for advanced open-vocabulary dense prediction.

Model-based Preference Optimization in Abstractive Summarization without Human Feedback

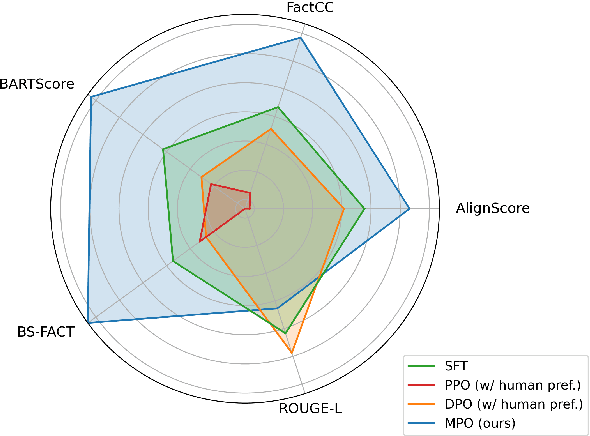
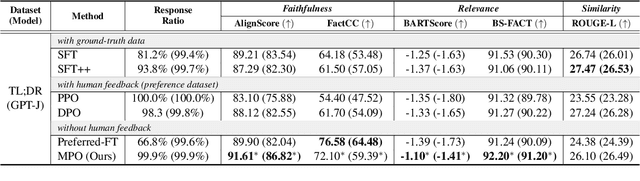
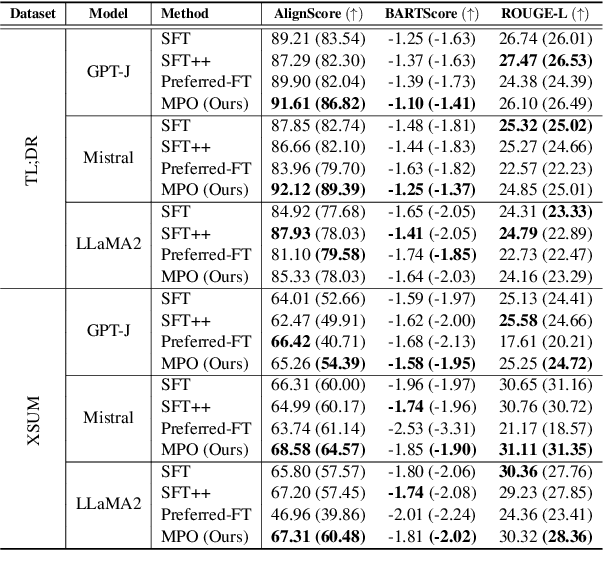
In abstractive summarization, the challenge of producing concise and accurate summaries arises from the vast amount of information contained in the source document. Consequently, although Large Language Models (LLMs) can generate fluent text, they often introduce inaccuracies by hallucinating content not found in the original source. While supervised fine-tuning methods that maximize likelihood contribute to this issue, they do not consistently enhance the faithfulness of the summaries. Preference-based optimization methods, such as Direct Preference Optimization (DPO), can further refine the model to align with human preferences. However, these methods still heavily depend on costly human feedback. In this work, we introduce a novel and straightforward approach called Model-based Preference Optimization (MPO) to fine-tune LLMs for improved summarization abilities without any human feedback. By leveraging the model's inherent summarization capabilities, we create a preference dataset that is fully generated by the model using different decoding strategies. Our experiments on standard summarization datasets and various metrics demonstrate that our proposed MPO significantly enhances the quality of generated summaries without relying on human feedback.

Modal Analysis of Spatiotemporal Data via Multivariate Gaussian Process Regression

Modal analysis has become an essential tool to understand the coherent structure of complex flows. The classical modal analysis methods, such as dynamic mode decomposition (DMD) and spectral proper orthogonal decomposition (SPOD), rely on a sufficient amount of data that is regularly sampled in time. However, often one needs to deal with sparse temporally irregular data, e.g., due to experimental measurements and simulation algorithm. To overcome the limitations of data scarcity and irregular sampling, we propose a novel modal analysis technique using multi-variate Gaussian process regression (MVGPR). We first establish the connection between MVGPR and the existing modal analysis techniques, DMD and SPOD, from a linear system identification perspective. Next, leveraging this connection, we develop a MVGPR-based modal analysis technique that addresses the aforementioned limitations. The capability of MVGPR is endowed by its judiciously designed kernel structure for correlation function, that is derived from the assumed linear dynamics. Subsequently, the proposed MVGPR method is benchmarked against DMD and SPOD on a range of examples, from academic and synthesized data to unsteady airfoil aerodynamics. The results demonstrate MVGPR as a promising alternative to classical modal analysis methods, especially in the scenario of scarce and temporally irregular data.