Learning Coarse-Grained Dynamics on Graph

We consider a Graph Neural Network (GNN) non-Markovian modeling framework to identify coarse-grained dynamical systems on graphs. Our main idea is to systematically determine the GNN architecture by inspecting how the leading term of the Mori-Zwanzig memory term depends on the coarse-grained interaction coefficients that encode the graph topology. Based on this analysis, we found that the appropriate GNN architecture that will account for $K$-hop dynamical interactions has to employ a Message Passing (MP) mechanism with at least $2K$ steps. We also deduce that the memory length required for an accurate closure model decreases as a function of the interaction strength under the assumption that the interaction strength exhibits a power law that decays as a function of the hop distance. Supporting numerical demonstrations on two examples, a heterogeneous Kuramoto oscillator model and a power system, suggest that the proposed GNN architecture can predict the coarse-grained dynamics under fixed and time-varying graph topologies.

Stationary Density Estimation of Itô Diffusions Using Deep Learning

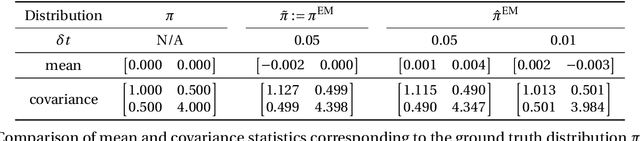
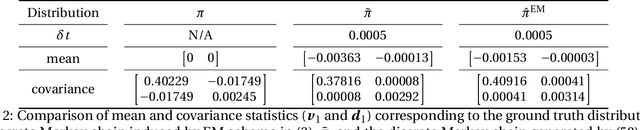
In this paper, we consider the density estimation problem associated with the stationary measure of ergodic It\^o diffusions from a discrete-time series that approximate the solutions of the stochastic differential equations. To take an advantage of the characterization of density function through the stationary solution of a parabolic-type Fokker-Planck PDE, we proceed as follows. First, we employ deep neural networks to approximate the drift and diffusion terms of the SDE by solving appropriate supervised learning tasks. Subsequently, we solve a steady-state Fokker-Plank equation associated with the estimated drift and diffusion coefficients with a neural-network-based least-squares method. We establish the convergence of the proposed scheme under appropriate mathematical assumptions, accounting for the generalization errors induced by regressing the drift and diffusion coefficients, and the PDE solvers. This theoretical study relies on a recent perturbation theory of Markov chain result that shows a linear dependence of the density estimation to the error in estimating the drift term, and generalization error results of nonparametric regression and of PDE regression solution obtained with neural-network models. The effectiveness of this method is reflected by numerical simulations of a two-dimensional Student's t distribution and a 20-dimensional Langevin dynamics.

Solving PDEs on Unknown Manifolds with Machine Learning

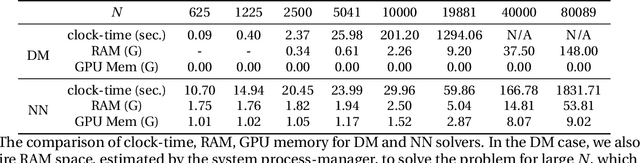
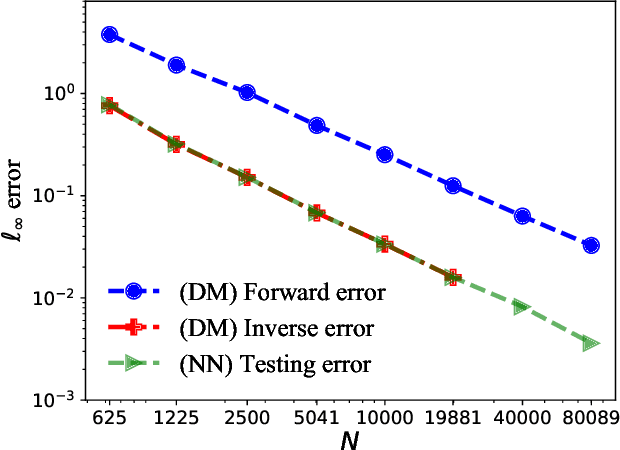
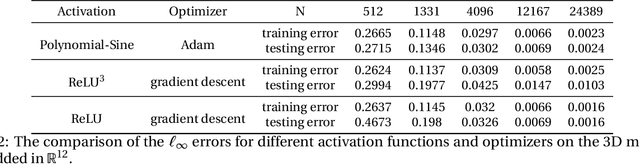
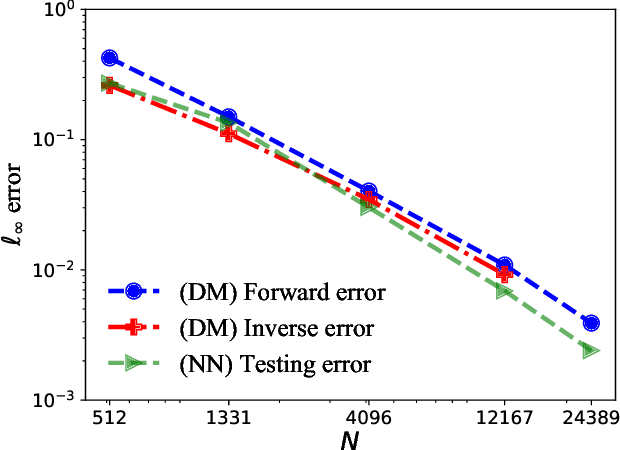
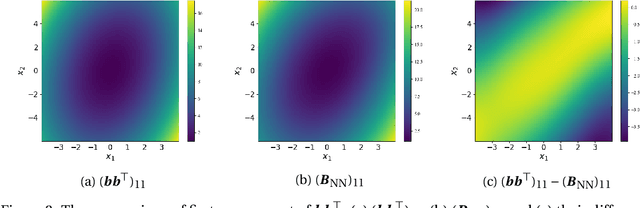
This paper proposes a mesh-free computational framework and machine learning theory for solving elliptic PDEs on unknown manifolds, identified with point clouds, based on diffusion maps (DM) and deep learning. The PDE solver is formulated as a supervised learning task to solve a least-squares regression problem that imposes an algebraic equation approximating a PDE (and boundary conditions if applicable). This algebraic equation involves a graph-Laplacian type matrix obtained via DM asymptotic expansion, which is a consistent estimator of second-order elliptic differential operators. The resulting numerical method is to solve a highly non-convex empirical risk minimization problem subjected to a solution from a hypothesis space of neural-network type functions. In a well-posed elliptic PDE setting, when the hypothesis space consists of feedforward neural networks with either infinite width or depth, we show that the global minimizer of the empirical loss function is a consistent solution in the limit of large training data. When the hypothesis space is a two-layer neural network, we show that for a sufficiently large width, the gradient descent method can identify a global minimizer of the empirical loss function. Supporting numerical examples demonstrate the convergence of the solutions and the effectiveness of the proposed solver in avoiding numerical issues that hampers the traditional approach when a large data set becomes available, e.g., large matrix inversion.

Error Bounds of the Invariant Statistics in Machine Learning of Ergodic Itô Diffusions

This paper studies the theoretical underpinnings of machine learning of ergodic It\^o diffusions. The objective is to understand the convergence properties of the invariant statistics when the underlying system of stochastic differential equations (SDEs) is empirically estimated with a supervised regression framework. Using the perturbation theory of ergodic Markov chains and the linear response theory, we deduce a linear dependence of the errors of one-point and two-point invariant statistics on the error in the learning of the drift and diffusion coefficients. More importantly, our study shows that the usual $L^2$-norm characterization of the learning generalization error is insufficient for achieving this linear dependence result. We find that sufficient conditions for such a linear dependence result are through learning algorithms that produce a uniformly Lipschitz and consistent estimator in the hypothesis space that retains certain characteristics of the drift coefficients, such as the usual linear growth condition that guarantees the existence of solutions of the underlying SDEs. We examine these conditions on two well-understood learning algorithms: the kernel-based spectral regression method and the shallow random neural networks with the ReLU activation function.

Machine Learning for Prediction with Missing Dynamics

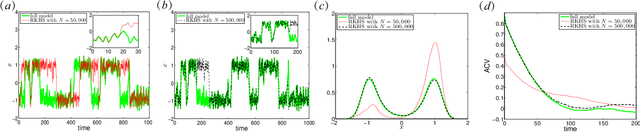
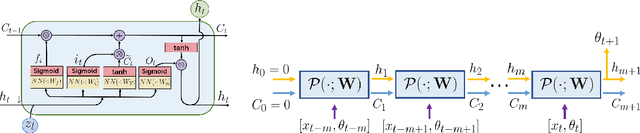
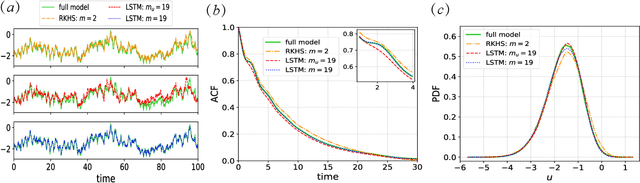
This article presents a general framework for recovering missing dynamical systems using available data and machine learning techniques. The proposed framework reformulates the prediction problem as a supervised learning problem to approximate a map that takes the memories of the resolved and identifiable unresolved variables to the missing components in the resolved dynamics. We demonstrate the effectiveness of the proposed framework with a theoretical guarantee of a path-wise convergence of the resolved variables up to finite time and numerical tests on prototypical models in various scientific domains. These include the 57-mode barotropic stress models with multiscale interactions that mimic the blocked and unblocked patterns observed in the atmosphere, the nonlinear Schr\"{o}dinger equation which found many applications in physics such as optics and Bose-Einstein-Condense, the Kuramoto-Sivashinsky equation which spatiotemporal chaotic pattern formation models trapped ion mode in plasma and phase dynamics in reaction-diffusion systems. While many machine learning techniques can be used to validate the proposed framework, we found that recurrent neural networks outperform kernel regression methods in terms of recovering the trajectory of the resolved components and the equilibrium one-point and two-point statistics. This superb performance suggests that recurrent neural networks are an effective tool for recovering the missing dynamics that involves approximation of high-dimensional functions.