Stochastic Quantum Sampling for Non-Logconcave Distributions and Estimating Partition Functions

We present quantum algorithms for sampling from non-logconcave probability distributions in the form of $\pi(x) \propto \exp(-\beta f(x))$. Here, $f$ can be written as a finite sum $f(x):= \frac{1}{N}\sum_{k=1}^N f_k(x)$. Our approach is based on quantum simulated annealing on slowly varying Markov chains derived from unadjusted Langevin algorithms, removing the necessity for function evaluations which can be computationally expensive for large data sets in mixture modeling and multi-stable systems. We also incorporate a stochastic gradient oracle that implements the quantum walk operators inexactly by only using mini-batch gradients. As a result, our stochastic gradient based algorithm only accesses small subsets of data points in implementing the quantum walk. One challenge of quantizing the resulting Markov chains is that they do not satisfy the detailed balance condition in general. Consequently, the mixing time of the algorithm cannot be expressed in terms of the spectral gap of the transition density, making the quantum algorithms nontrivial to analyze. To overcome these challenges, we first build a hypothetical Markov chain that is reversible, and also converges to the target distribution. Then, we quantified the distance between our algorithm's output and the target distribution by using this hypothetical chain as a bridge to establish the total complexity. Our quantum algorithms exhibit polynomial speedups in terms of both dimension and precision dependencies when compared to the best-known classical algorithms.

Efficient Quantum Algorithms for Quantum Optimal Control

In this paper, we present efficient quantum algorithms that are exponentially faster than classical algorithms for solving the quantum optimal control problem. This problem involves finding the control variable that maximizes a physical quantity at time $T$, where the system is governed by a time-dependent Schr\"odinger equation. This type of control problem also has an intricate relation with machine learning. Our algorithms are based on a time-dependent Hamiltonian simulation method and a fast gradient-estimation algorithm. We also provide a comprehensive error analysis to quantify the total error from various steps, such as the finite-dimensional representation of the control function, the discretization of the Schr\"odinger equation, the numerical quadrature, and optimization. Our quantum algorithms require fault-tolerant quantum computers.

The Mori-Zwanzig formulation of deep learning

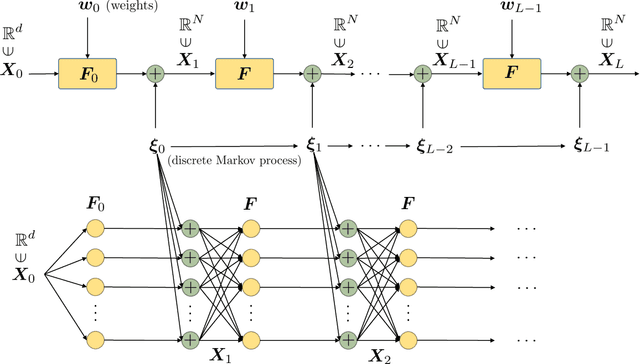
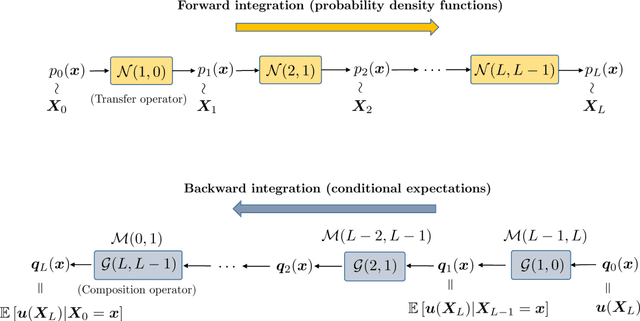
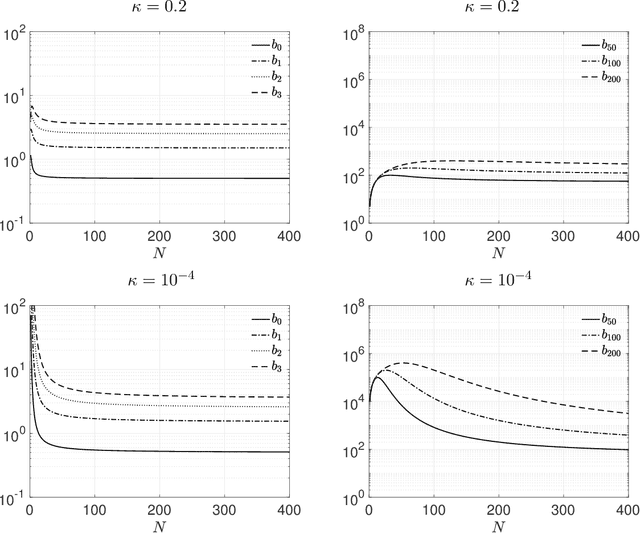
We develop a new formulation of deep learning based on the Mori-Zwanzig (MZ) formalism of irreversible statistical mechanics. The new formulation is built upon the well-known duality between deep neural networks and discrete stochastic dynamical systems, and it allows us to directly propagate quantities of interest (conditional expectations and probability density functions) forward and backward through the network by means of exact linear operator equations. Such new equations can be used as a starting point to develop new effective parameterizations of deep neural networks, and provide a new framework to study deep-learning via operator theoretic methods. The proposed MZ formulation of deep learning naturally introduces a new concept, i.e., the memory of the neural network, which plays a fundamental role in low-dimensional modeling and parameterization. By using the theory of contraction mappings, we develop sufficient conditions for the memory of the neural network to decay with the number of layers. This allows us to rigorously transform deep networks into shallow ones, e.g., by reducing the number of neurons per layer (using projection operators), or by reducing the total number of layers (using the decay property of the memory operator).

Stability Preserving Data-driven Models With Latent Dynamics

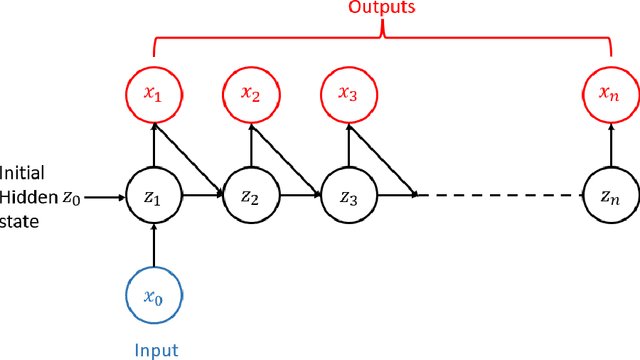
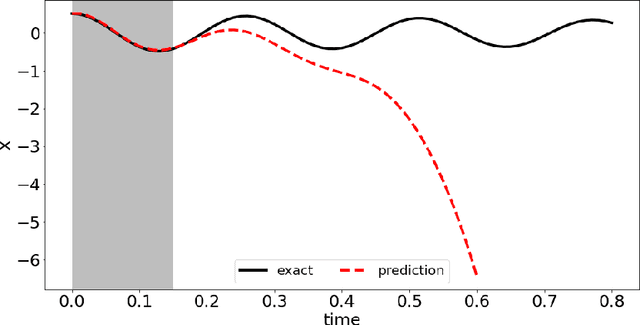
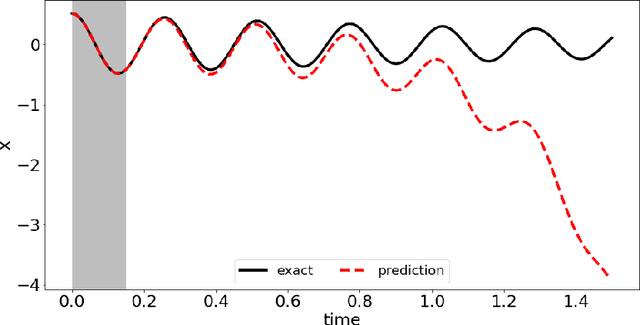
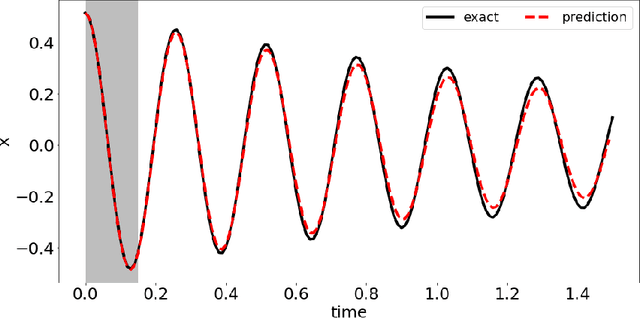
In this paper, we introduce a data-driven modeling approach for dynamics problems with latent variables. The state-space of the proposed model includes artificial latent variables, in addition to observed variables that can be fitted to a given data set. We present a model framework where the stability of the coupled dynamics can be easily enforced. The model is implemented by recurrent cells and trained using backpropagation through time. Numerical examples using benchmark tests from order reduction problems demonstrate the stability of the model and the efficiency of the recurrent cell implementation. As applications, two fluid-structure interaction problems are considered to illustrate the accuracy and predictive capability of the model.

A Local Convergence Theory for the Stochastic Gradient Descent Method in Non-Convex Optimization With Non-isolated Local Minima

Non-convex loss functions arise frequently in modern machine learning, and for the theoretical analysis of stochastic optimization methods, the presence of non-isolated minima presents a unique challenge that has remained under-explored. In this paper, we study the local convergence of the stochastic gradient descent method to non-isolated global minima. Under mild assumptions, we estimate the probability for the iterations to stay near the minima by adopting the notion of stochastic stability. After establishing such stability, we present the lower bound complexity in terms of various error criteria for a given error tolerance $\epsilon$ and a failure probability $\gamma$.

Error Bounds of the Invariant Statistics in Machine Learning of Ergodic Itô Diffusions

This paper studies the theoretical underpinnings of machine learning of ergodic It\^o diffusions. The objective is to understand the convergence properties of the invariant statistics when the underlying system of stochastic differential equations (SDEs) is empirically estimated with a supervised regression framework. Using the perturbation theory of ergodic Markov chains and the linear response theory, we deduce a linear dependence of the errors of one-point and two-point invariant statistics on the error in the learning of the drift and diffusion coefficients. More importantly, our study shows that the usual $L^2$-norm characterization of the learning generalization error is insufficient for achieving this linear dependence result. We find that sufficient conditions for such a linear dependence result are through learning algorithms that produce a uniformly Lipschitz and consistent estimator in the hypothesis space that retains certain characteristics of the drift coefficients, such as the usual linear growth condition that guarantees the existence of solutions of the underlying SDEs. We examine these conditions on two well-understood learning algorithms: the kernel-based spectral regression method and the shallow random neural networks with the ReLU activation function.