Yushuang Luo
Stability Preserving Data-driven Models With Latent Dynamics
Apr 20, 2022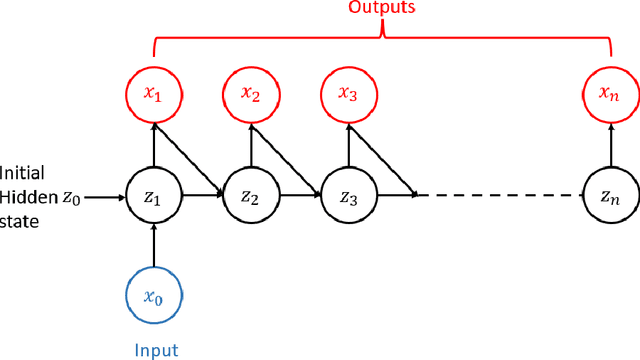
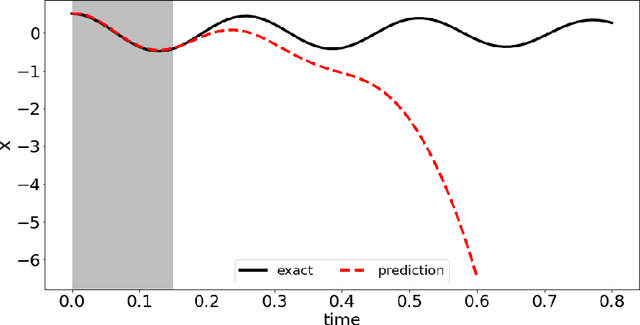
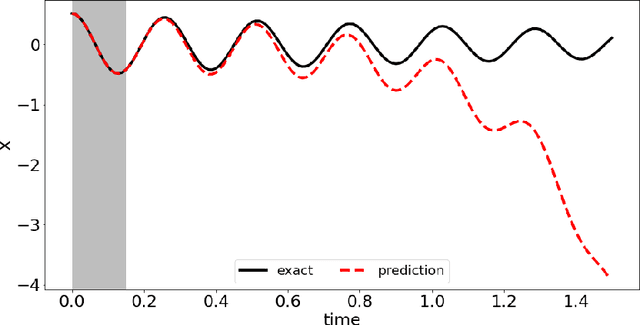
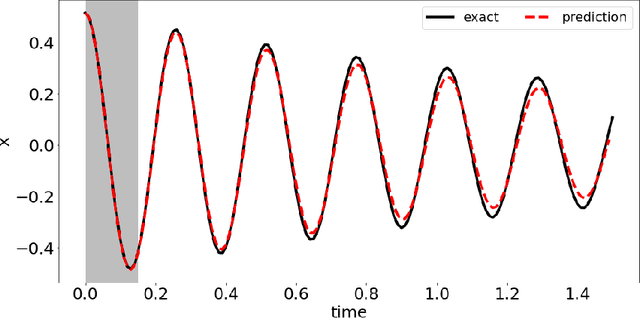
Abstract:In this paper, we introduce a data-driven modeling approach for dynamics problems with latent variables. The state-space of the proposed model includes artificial latent variables, in addition to observed variables that can be fitted to a given data set. We present a model framework where the stability of the coupled dynamics can be easily enforced. The model is implemented by recurrent cells and trained using backpropagation through time. Numerical examples using benchmark tests from order reduction problems demonstrate the stability of the model and the efficiency of the recurrent cell implementation. As applications, two fluid-structure interaction problems are considered to illustrate the accuracy and predictive capability of the model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge