Daniele Venturi
Uncertainty propagation in feed-forward neural network models
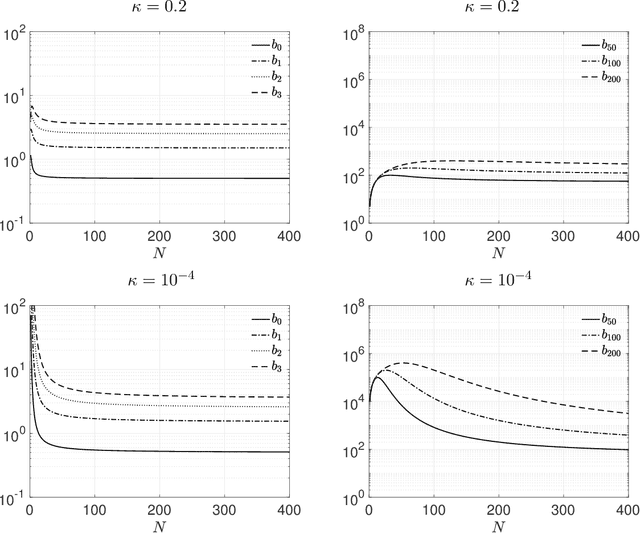
Mar 27, 2025Abstract:We develop new uncertainty propagation methods for feed-forward neural network architectures with leaky ReLu activation functions subject to random perturbations in the input vectors. In particular, we derive analytical expressions for the probability density function (PDF) of the neural network output and its statistical moments as a function of the input uncertainty and the parameters of the network, i.e., weights and biases. A key finding is that an appropriate linearization of the leaky ReLu activation function yields accurate statistical results even for large perturbations in the input vectors. This can be attributed to the way information propagates through the network. We also propose new analytically tractable Gaussian copula surrogate models to approximate the full joint PDF of the neural network output. To validate our theorical results, we conduct Monte Carlo simulations and a thorough error analysis on a multi-layer neural network representing a nonlinear integro-differential operator between two polynomial function spaces. Our findings demonstrate excellent agreement between the theoretical predictions and Monte Carlo simulations.
Watermarks in the Sand: Impossibility of Strong Watermarking for Generative Models
Nov 15, 2023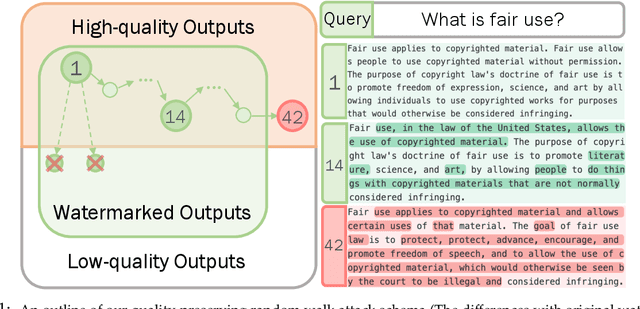

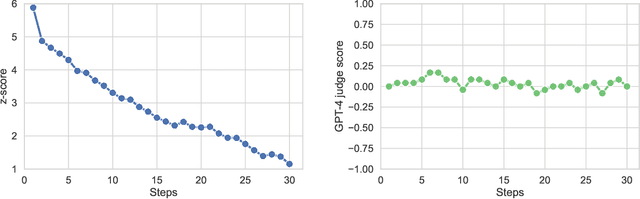

Abstract:Watermarking generative models consists of planting a statistical signal (watermark) in a model's output so that it can be later verified that the output was generated by the given model. A strong watermarking scheme satisfies the property that a computationally bounded attacker cannot erase the watermark without causing significant quality degradation. In this paper, we study the (im)possibility of strong watermarking schemes. We prove that, under well-specified and natural assumptions, strong watermarking is impossible to achieve. This holds even in the private detection algorithm setting, where the watermark insertion and detection algorithms share a secret key, unknown to the attacker. To prove this result, we introduce a generic efficient watermark attack; the attacker is not required to know the private key of the scheme or even which scheme is used. Our attack is based on two assumptions: (1) The attacker has access to a "quality oracle" that can evaluate whether a candidate output is a high-quality response to a prompt, and (2) The attacker has access to a "perturbation oracle" which can modify an output with a nontrivial probability of maintaining quality, and which induces an efficiently mixing random walk on high-quality outputs. We argue that both assumptions can be satisfied in practice by an attacker with weaker computational capabilities than the watermarked model itself, to which the attacker has only black-box access. Furthermore, our assumptions will likely only be easier to satisfy over time as models grow in capabilities and modalities. We demonstrate the feasibility of our attack by instantiating it to attack three existing watermarking schemes for large language models: Kirchenbauer et al. (2023), Kuditipudi et al. (2023), and Zhao et al. (2023). The same attack successfully removes the watermarks planted by all three schemes, with only minor quality degradation.
The Mori-Zwanzig formulation of deep learning
Sep 15, 2022
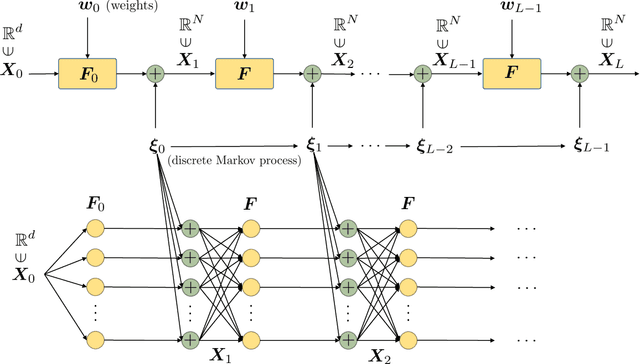
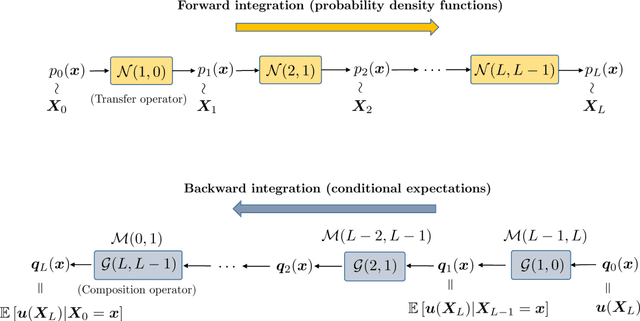
Abstract:We develop a new formulation of deep learning based on the Mori-Zwanzig (MZ) formalism of irreversible statistical mechanics. The new formulation is built upon the well-known duality between deep neural networks and discrete stochastic dynamical systems, and it allows us to directly propagate quantities of interest (conditional expectations and probability density functions) forward and backward through the network by means of exact linear operator equations. Such new equations can be used as a starting point to develop new effective parameterizations of deep neural networks, and provide a new framework to study deep-learning via operator theoretic methods. The proposed MZ formulation of deep learning naturally introduces a new concept, i.e., the memory of the neural network, which plays a fundamental role in low-dimensional modeling and parameterization. By using the theory of contraction mappings, we develop sufficient conditions for the memory of the neural network to decay with the number of layers. This allows us to rigorously transform deep networks into shallow ones, e.g., by reducing the number of neurons per layer (using projection operators), or by reducing the total number of layers (using the decay property of the memory operator).
Improving neural network predictions of material properties with limited data using transfer learning
Jun 29, 2020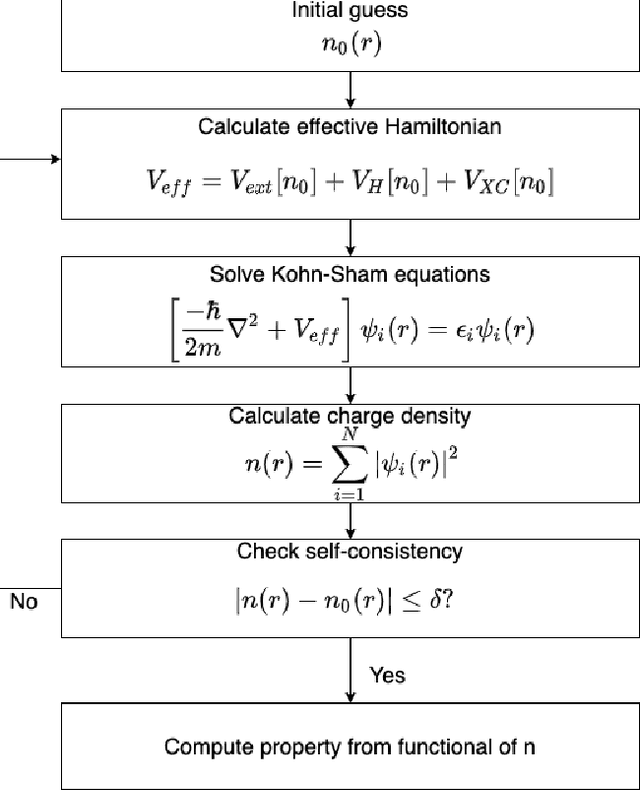
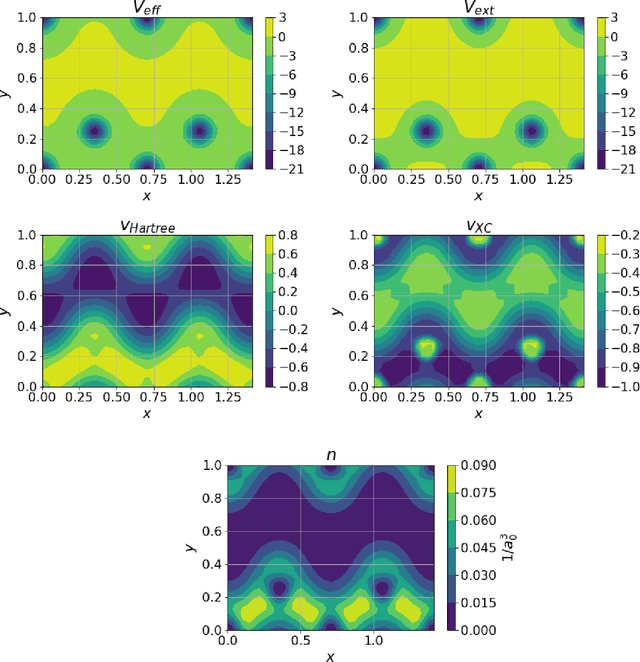


Abstract:We develop new transfer learning algorithms to accelerate prediction of material properties from ab initio simulations based on density functional theory (DFT). Transfer learning has been successfully utilized for data-efficient modeling in applications other than materials science, and it allows transferable representations learned from large datasets to be repurposed for learning new tasks even with small datasets. In the context of materials science, this opens the possibility to develop generalizable neural network models that can be repurposed on other materials, without the need of generating a large (computationally expensive) training set of materials properties. The proposed transfer learning algorithms are demonstrated on predicting the Gibbs free energy of light transition metal oxides.
Density Propagation with Characteristics-based Deep Learning
Nov 21, 2019
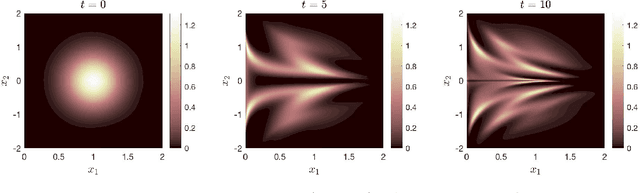
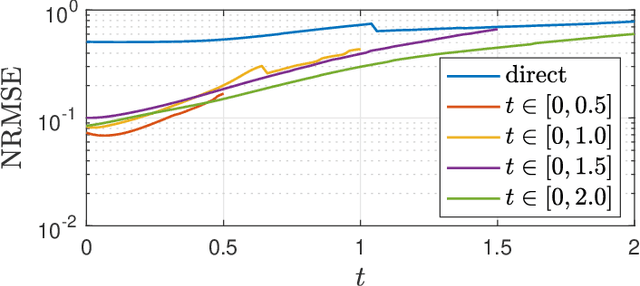

Abstract:Uncertainty propagation in nonlinear dynamic systems remains an outstanding problem in scientific computing and control. Numerous approaches have been developed, but are limited in their capability to tackle problems with more than a few uncertain variables or require large amounts of simulation data. In this paper, we propose a data-driven method for approximating joint probability density functions (PDFs) of nonlinear dynamic systems with initial condition and parameter uncertainty. Our approach leverages on the power of deep learning to deal with high-dimensional inputs, but we overcome the need for huge quantities of training data by encoding PDF evolution equations directly into the optimization problem. We demonstrate the potential of the proposed method by applying it to evaluate the robustness of a feedback controller for a six-dimensional rigid body with parameter uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge