Qi Gong
HiPreNets: High-Precision Neural Networks through Progressive Training
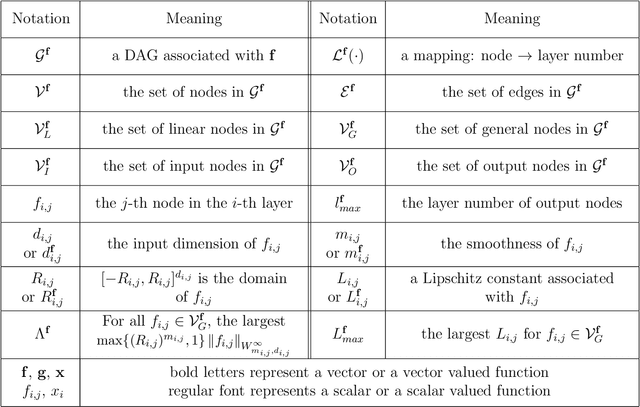
Jun 18, 2025Abstract:Deep neural networks are powerful tools for solving nonlinear problems in science and engineering, but training highly accurate models becomes challenging as problem complexity increases. Non-convex optimization and numerous hyperparameters to tune make performance improvement difficult, and traditional approaches often prioritize minimizing mean squared error (MSE) while overlooking $L^{\infty}$ error, which is the critical focus in many applications. To address these challenges, we present a progressive framework for training and tuning high-precision neural networks (HiPreNets). Our approach refines a previously explored staged training technique for neural networks that improves an existing fully connected neural network by sequentially learning its prediction residuals using additional networks, leading to improved overall accuracy. We discuss how to take advantage of the structure of the residuals to guide the choice of loss function, number of parameters to use, and ways to introduce adaptive data sampling techniques. We validate our framework's effectiveness through several benchmark problems.
Neural Network Optimal Feedback Control with Guaranteed Local Stability
May 01, 2022



Abstract:Recent research shows that deep learning can be an effective tool for designing optimal feedback controllers for high-dimensional nonlinear dynamic systems. But the behavior of these neural network (NN) controllers is still not well understood. In particular, some NNs with high test accuracy can fail to even locally stabilize the dynamic system. To address this challenge we propose several novel NN architectures, which we show guarantee local stability while retaining the semi-global approximation capacity to learn the optimal feedback policy. The proposed architectures are compared against standard NN feedback controllers through numerical simulations of two high-dimensional nonlinear optimal control problems (OCPs): stabilization of an unstable Burgers-type partial differential equation (PDE), and altitude and course tracking for a six degree-of-freedom (6DoF) unmanned aerial vehicle (UAV). The simulations demonstrate that standard NNs can fail to stabilize the dynamics even when trained well, while the proposed architectures are always at least locally stable. Moreover, the proposed controllers are found to be near-optimal in testing.
Neural network optimal feedback control with enhanced closed loop stability
Sep 15, 2021
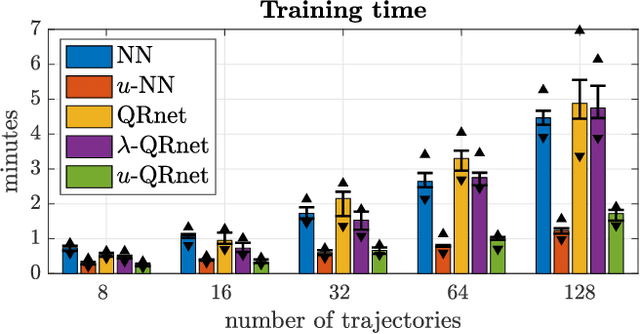
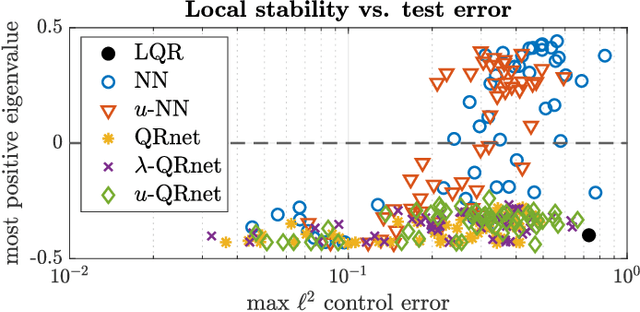
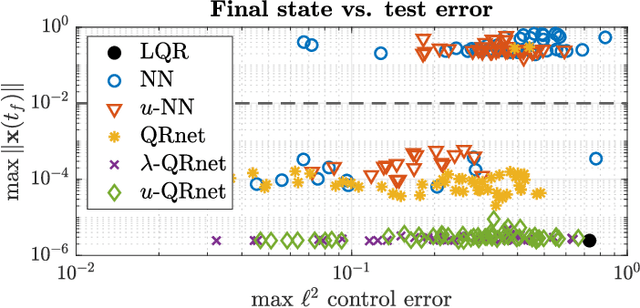
Abstract:Recent research has shown that supervised learning can be an effective tool for designing optimal feedback controllers for high-dimensional nonlinear dynamic systems. But the behavior of these neural network (NN) controllers is still not well understood. In this paper we use numerical simulations to demonstrate that typical test accuracy metrics do not effectively capture the ability of an NN controller to stabilize a system. In particular, some NNs with high test accuracy can fail to stabilize the dynamics. To address this we propose two NN architectures which locally approximate a linear quadratic regulator (LQR). Numerical simulations confirm our intuition that the proposed architectures reliably produce stabilizing feedback controllers without sacrificing performance. In addition, we introduce a preliminary theoretical result describing some stability properties of such NN-controlled systems.
Neural Network Approximations of Compositional Functions With Applications to Dynamical Systems
Dec 03, 2020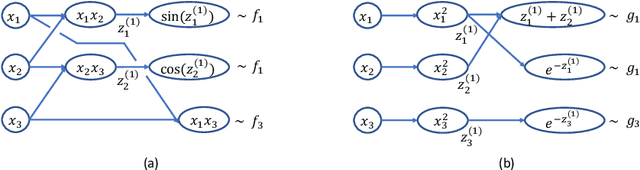
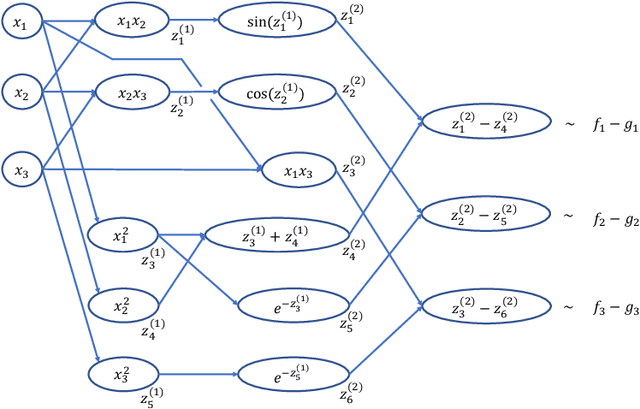
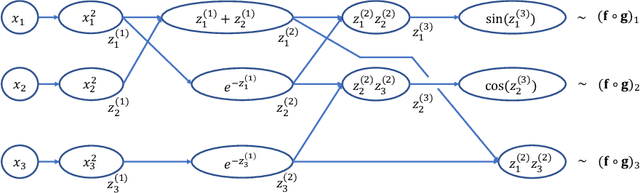
Abstract:As demonstrated in many areas of real-life applications, neural networks have the capability of dealing with high dimensional data. In the fields of optimal control and dynamical systems, the same capability was studied and verified in many published results in recent years. Towards the goal of revealing the underlying reason why neural networks are capable of solving some high dimensional problems, we develop an algebraic framework and an approximation theory for compositional functions and their neural network approximations. The theoretical foundation is developed in a way so that it supports the error analysis for not only functions as input-output relations, but also numerical algorithms. This capability is critical because it enables the analysis of approximation errors for problems for which analytic solutions are not available, such as differential equations and optimal control. We identify a set of key features of compositional functions and the relationship between the features and the complexity of neural networks. In addition to function approximations, we prove several formulae of error upper bounds for neural networks that approximate the solutions to differential equations, optimization, and optimal control.
QRnet: optimal regulator design with LQR-augmented neural networks
Sep 11, 2020


Abstract:In this paper we propose a new computational method for designing optimal regulators for high-dimensional nonlinear systems. The proposed approach leverages physics-informed machine learning to solve high-dimensional Hamilton-Jacobi-Bellman equations arising in optimal feedback control. Concretely, we augment linear quadratic regulators with neural networks to handle nonlinearities. We train the augmented models on data generated without discretizing the state space, enabling application to high-dimensional problems. We use the proposed method to design a candidate optimal regulator for an unstable Burgers' equation, and through this example, demonstrate improved robustness and accuracy compared to existing neural network formulations.
Density Propagation with Characteristics-based Deep Learning
Nov 21, 2019
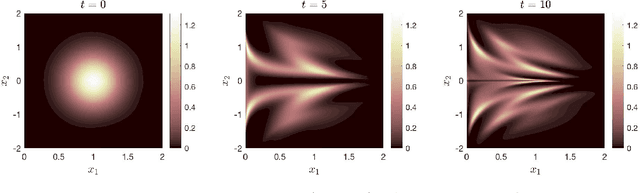

Abstract:Uncertainty propagation in nonlinear dynamic systems remains an outstanding problem in scientific computing and control. Numerous approaches have been developed, but are limited in their capability to tackle problems with more than a few uncertain variables or require large amounts of simulation data. In this paper, we propose a data-driven method for approximating joint probability density functions (PDFs) of nonlinear dynamic systems with initial condition and parameter uncertainty. Our approach leverages on the power of deep learning to deal with high-dimensional inputs, but we overcome the need for huge quantities of training data by encoding PDF evolution equations directly into the optimization problem. We demonstrate the potential of the proposed method by applying it to evaluate the robustness of a feedback controller for a six-dimensional rigid body with parameter uncertainty.
Adaptive Deep Learning for High Dimensional Hamilton-Jacobi-Bellman Equations
Jul 12, 2019



Abstract:Computing optimal feedback controls for nonlinear systems generally requires solving Hamilton-Jacobi-Bellman (HJB) equations, which, in high dimensions, are notoriously difficult. Existing strategies for high dimensional problems generally rely on specific, restrictive problem structures, or are valid only locally around some nominal trajectory. In this paper, we propose a data-driven method to approximate semi-global solutions to HJB equations for general high dimensional nonlinear systems and compute optimal feedback controls in real-time. To accomplish this, we model solutions to HJB equations with neural networks (NNs) trained on data generated independently of any state space discretization. Training is made more effective and efficient by leveraging the known physics of the problem and using the partially trained NN to aid in adaptive data generation. We demonstrate the effectiveness of our method by learning the approximate solution to the HJB equation corresponding to the stabilization of six dimensional nonlinear rigid body, and controlling the system with the trained NN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge