Neural Network Approximations of Compositional Functions With Applications to Dynamical Systems
Paper and Code
Dec 03, 2020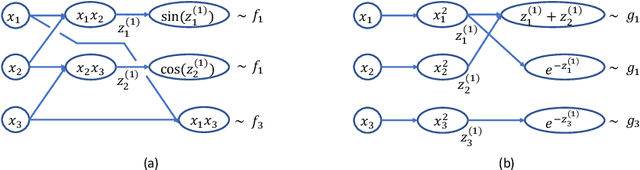
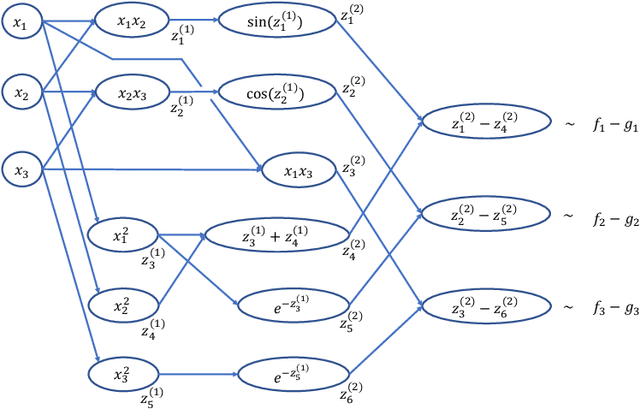
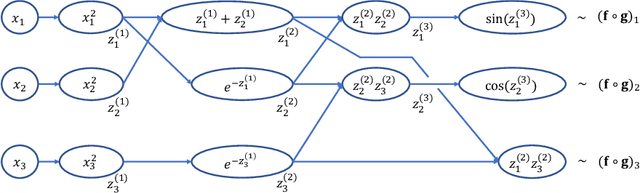
As demonstrated in many areas of real-life applications, neural networks have the capability of dealing with high dimensional data. In the fields of optimal control and dynamical systems, the same capability was studied and verified in many published results in recent years. Towards the goal of revealing the underlying reason why neural networks are capable of solving some high dimensional problems, we develop an algebraic framework and an approximation theory for compositional functions and their neural network approximations. The theoretical foundation is developed in a way so that it supports the error analysis for not only functions as input-output relations, but also numerical algorithms. This capability is critical because it enables the analysis of approximation errors for problems for which analytic solutions are not available, such as differential equations and optimal control. We identify a set of key features of compositional functions and the relationship between the features and the complexity of neural networks. In addition to function approximations, we prove several formulae of error upper bounds for neural networks that approximate the solutions to differential equations, optimization, and optimal control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge