Challenges Faced by Large Language Models in Solving Multi-Agent Flocking

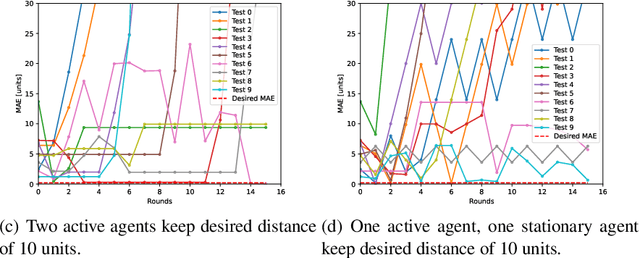
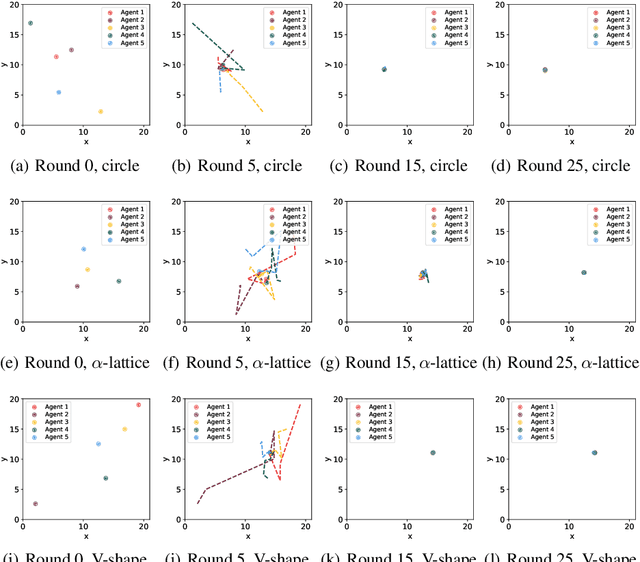
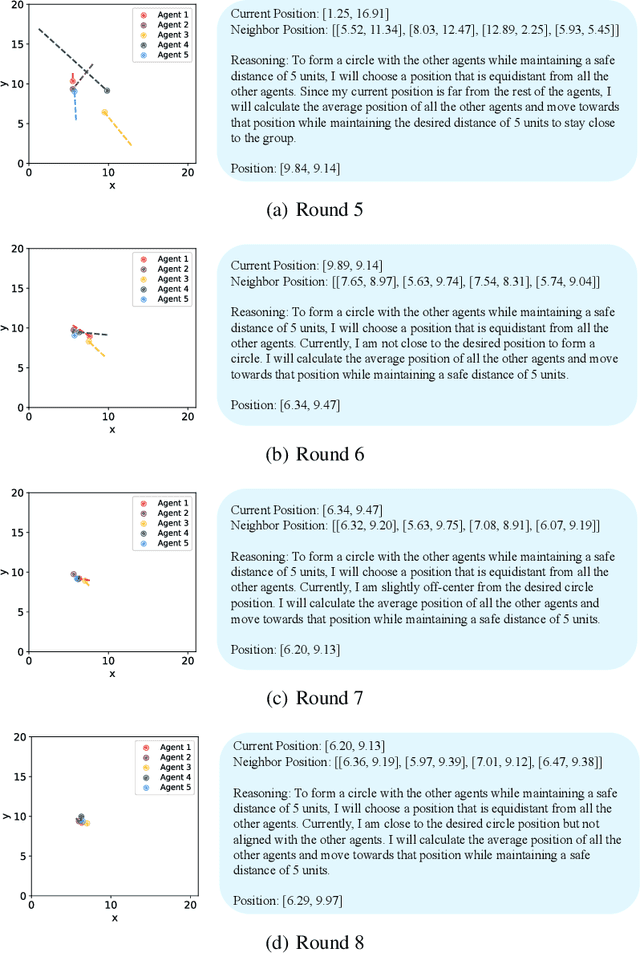
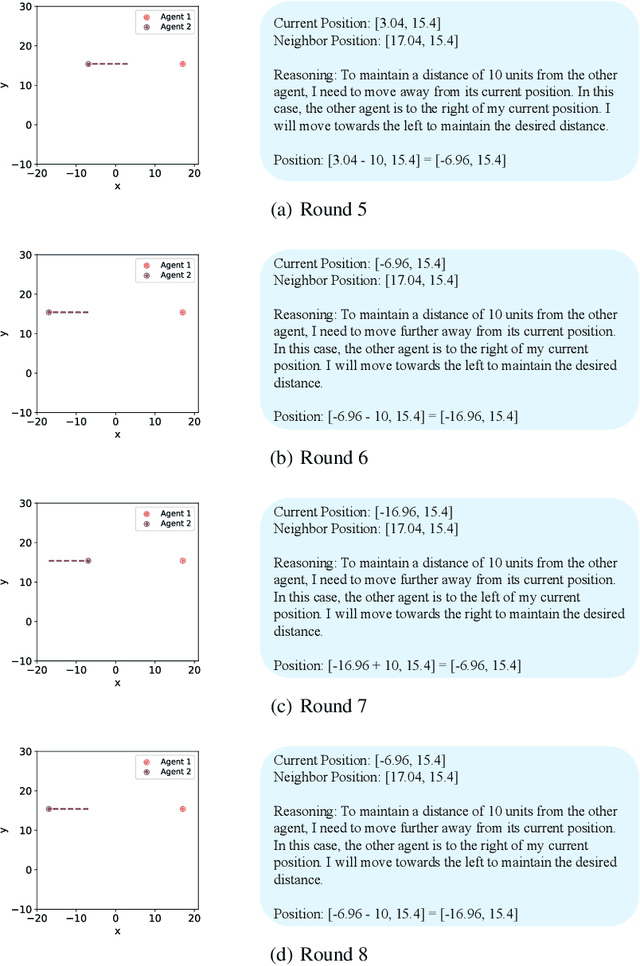
Flocking is a behavior where multiple agents in a system attempt to stay close to each other while avoiding collision and maintaining a desired formation. This is observed in the natural world and has applications in robotics, including natural disaster search and rescue, wild animal tracking, and perimeter surveillance and patrol. Recently, large language models (LLMs) have displayed an impressive ability to solve various collaboration tasks as individual decision-makers. Solving multi-agent flocking with LLMs would demonstrate their usefulness in situations requiring spatial and decentralized decision-making. Yet, when LLM-powered agents are tasked with implementing multi-agent flocking, they fall short of the desired behavior. After extensive testing, we find that agents with LLMs as individual decision-makers typically opt to converge on the average of their initial positions or diverge from each other. After breaking the problem down, we discover that LLMs cannot understand maintaining a shape or keeping a distance in a meaningful way. Solving multi-agent flocking with LLMs would enhance their ability to understand collaborative spatial reasoning and lay a foundation for addressing more complex multi-agent tasks. This paper discusses the challenges LLMs face in multi-agent flocking and suggests areas for future improvement and research.

Few-Shot Domain Adaptation with Polymorphic Transformers

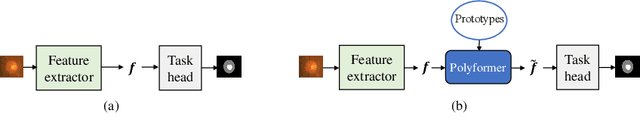
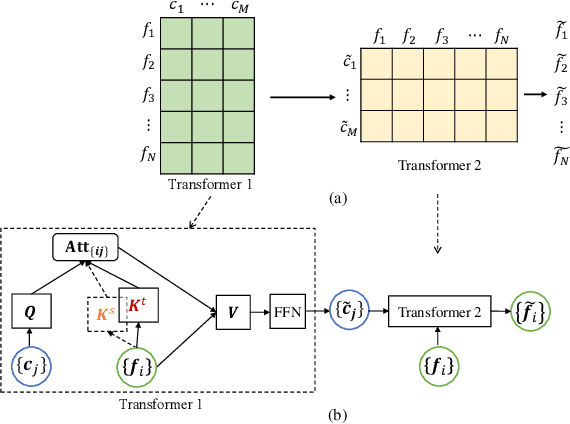
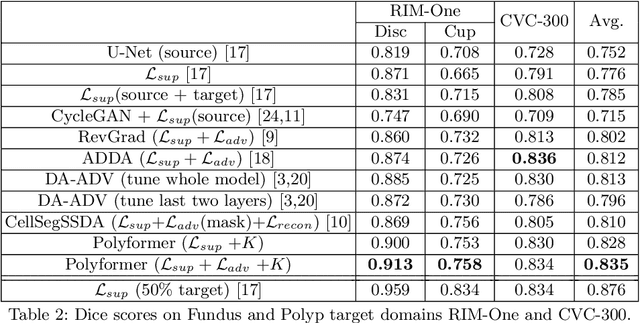
Deep neural networks (DNNs) trained on one set of medical images often experience severe performance drop on unseen test images, due to various domain discrepancy between the training images (source domain) and the test images (target domain), which raises a domain adaptation issue. In clinical settings, it is difficult to collect enough annotated target domain data in a short period. Few-shot domain adaptation, i.e., adapting a trained model with a handful of annotations, is highly practical and useful in this case. In this paper, we propose a Polymorphic Transformer (Polyformer), which can be incorporated into any DNN backbones for few-shot domain adaptation. Specifically, after the polyformer layer is inserted into a model trained on the source domain, it extracts a set of prototype embeddings, which can be viewed as a "basis" of the source-domain features. On the target domain, the polyformer layer adapts by only updating a projection layer which controls the interactions between image features and the prototype embeddings. All other model weights (except BatchNorm parameters) are frozen during adaptation. Thus, the chance of overfitting the annotations is greatly reduced, and the model can perform robustly on the target domain after being trained on a few annotated images. We demonstrate the effectiveness of Polyformer on two medical segmentation tasks (i.e., optic disc/cup segmentation, and polyp segmentation). The source code of Polyformer is released at https://github.com/askerlee/segtran.

Manifold Learning via Manifold Deflation

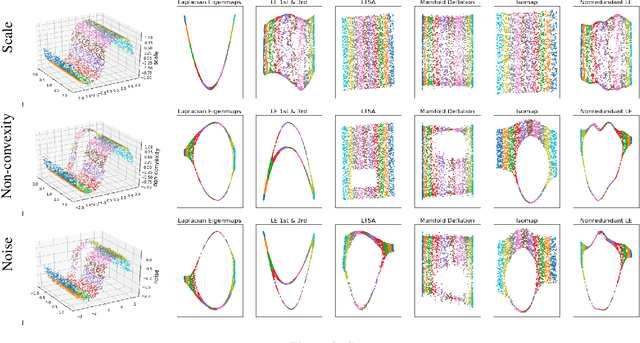
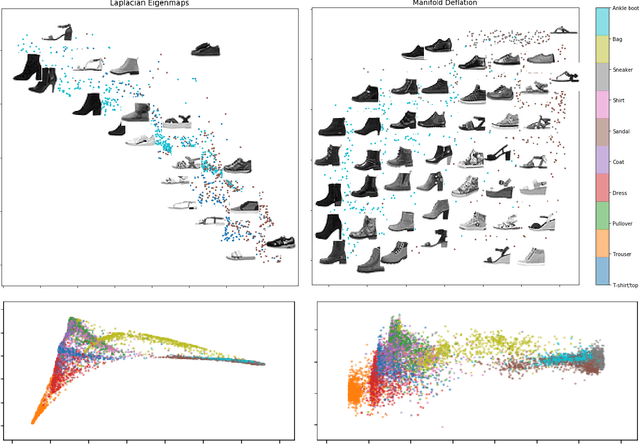
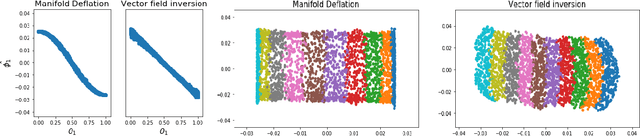
Nonlinear dimensionality reduction methods provide a valuable means to visualize and interpret high-dimensional data. However, many popular methods can fail dramatically, even on simple two-dimensional manifolds, due to problems such as vulnerability to noise, repeated eigendirections, holes in convex bodies, and boundary bias. We derive an embedding method for Riemannian manifolds that iteratively uses single-coordinate estimates to eliminate dimensions from an underlying differential operator, thus "deflating" it. These differential operators have been shown to characterize any local, spectral dimensionality reduction method. The key to our method is a novel, incremental tangent space estimator that incorporates global structure as coordinates are added. We prove its consistency when the coordinates converge to true coordinates. Empirically, we show our algorithm recovers novel and interesting embeddings on real-world and synthetic datasets.

On Nonlinear Dimensionality Reduction, Linear Smoothing and Autoencoding

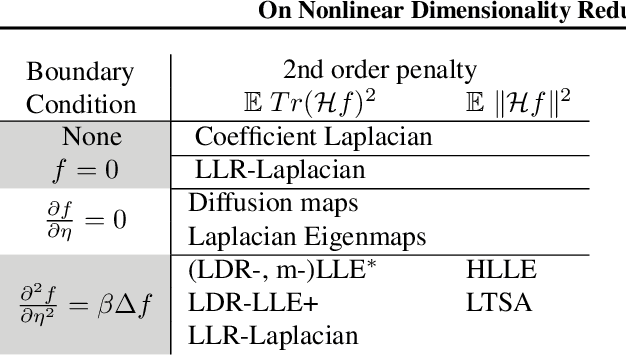
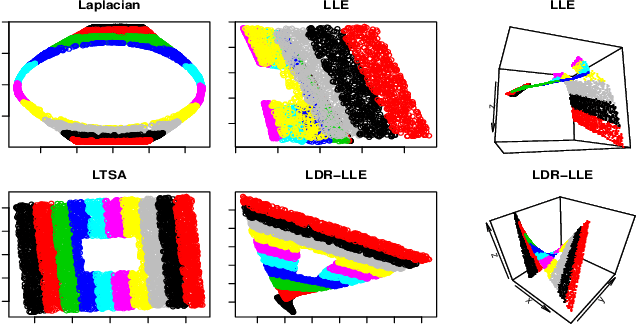
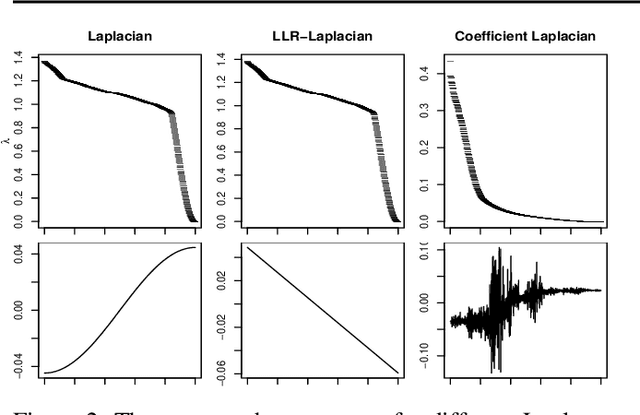
We develop theory for nonlinear dimensionality reduction (NLDR). A number of NLDR methods have been developed, but there is limited understanding of how these methods work and the relationships between them. There is limited basis for using existing NLDR theory for deriving new algorithms. We provide a novel framework for analysis of NLDR via a connection to the statistical theory of linear smoothers. This allows us to both understand existing methods and derive new ones. We use this connection to smoothing to show that asymptotically, existing NLDR methods correspond to discrete approximations of the solutions of sets of differential equations given a boundary condition. In particular, we can characterize many existing methods in terms of just three limiting differential operators and boundary conditions. Our theory also provides a way to assert that one method is preferable to another; indeed, we show Local Tangent Space Alignment is superior within a class of methods that assume a global coordinate chart defines an isometric embedding of the manifold.

Optimal Sub-sampling with Influence Functions

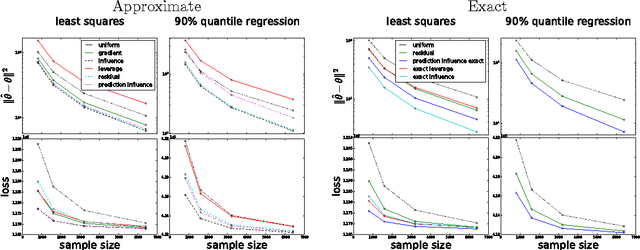
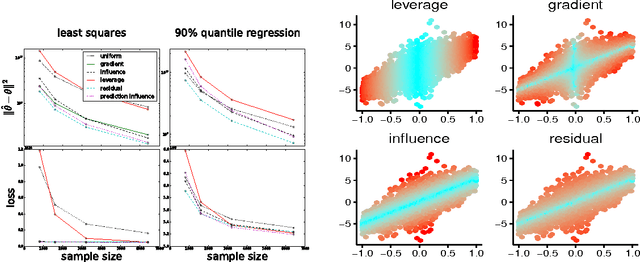
Sub-sampling is a common and often effective method to deal with the computational challenges of large datasets. However, for most statistical models, there is no well-motivated approach for drawing a non-uniform subsample. We show that the concept of an asymptotically linear estimator and the associated influence function leads to optimal sampling procedures for a wide class of popular models. Furthermore, for linear regression models which have well-studied procedures for non-uniform sub-sampling, we show our optimal influence function based method outperforms previous approaches. We empirically show the improved performance of our method on real datasets.

Adaptive Threshold Sampling and Estimation

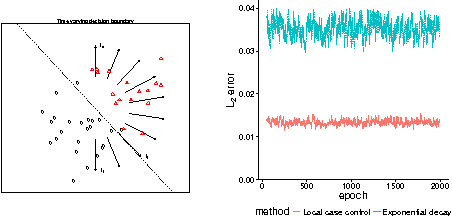
Sampling is a fundamental problem in both computer science and statistics. A number of issues arise when designing a method based on sampling. These include statistical considerations such as constructing a good sampling design and ensuring there are good, tractable estimators for the quantities of interest as well as computational considerations such as designing fast algorithms for streaming data and ensuring the sample fits within memory constraints. Unfortunately, existing sampling methods are only able to address all of these issues in limited scenarios. We develop a framework that can be used to address these issues in a broad range of scenarios. In particular, it addresses the problem of drawing and using samples under some memory budget constraint. This problem can be challenging since the memory budget forces samples to be drawn non-independently and consequently, makes computation of resulting estimators difficult. At the core of the framework is the notion of a data adaptive thresholding scheme where the threshold effectively allows one to treat the non-independent sample as if it were drawn independently. We provide sufficient conditions for a thresholding scheme to allow this and provide ways to build and compose such schemes. Furthermore, we provide fast algorithms to efficiently sample under these thresholding schemes.

Online Semi-Supervised Learning on Quantized Graphs

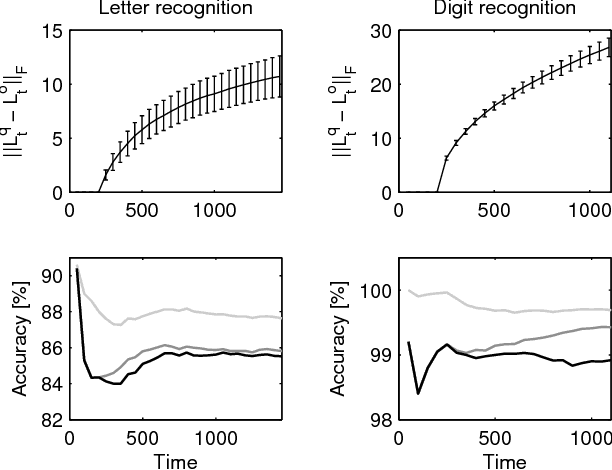
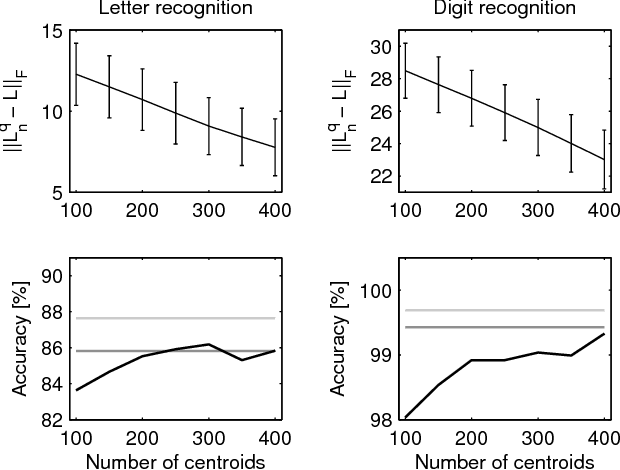
In this paper, we tackle the problem of online semi-supervised learning (SSL). When data arrive in a stream, the dual problems of computation and data storage arise for any SSL method. We propose a fast approximate online SSL algorithm that solves for the harmonic solution on an approximate graph. We show, both empirically and theoretically, that good behavior can be achieved by collapsing nearby points into a set of local "representative points" that minimize distortion. Moreover, we regularize the harmonic solution to achieve better stability properties. We apply our algorithm to face recognition and optical character recognition applications to show that we can take advantage of the manifold structure to outperform the previous methods. Unlike previous heuristic approaches, we show that our method yields provable performance bounds.

An Analysis of the Convergence of Graph Laplacians

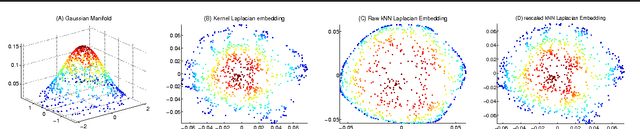
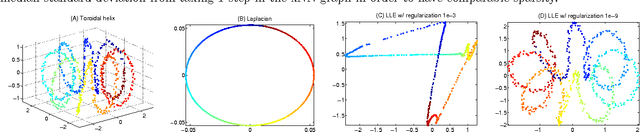
Existing approaches to analyzing the asymptotics of graph Laplacians typically assume a well-behaved kernel function with smoothness assumptions. We remove the smoothness assumption and generalize the analysis of graph Laplacians to include previously unstudied graphs including kNN graphs. We also introduce a kernel-free framework to analyze graph constructions with shrinking neighborhoods in general and apply it to analyze locally linear embedding (LLE). We also describe how for a given limiting Laplacian operator desirable properties such as a convergent spectrum and sparseness can be achieved choosing the appropriate graph construction.