Manifold Learning via Manifold Deflation
Paper and Code
Jul 07, 2020
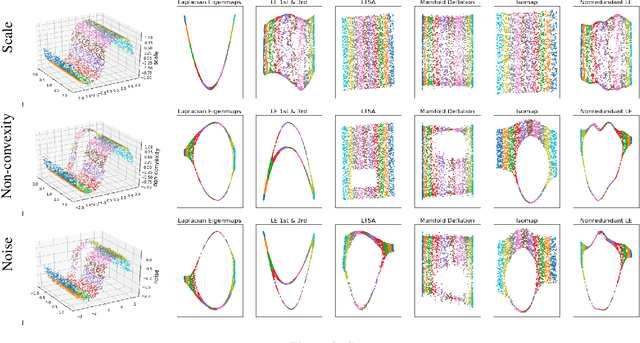
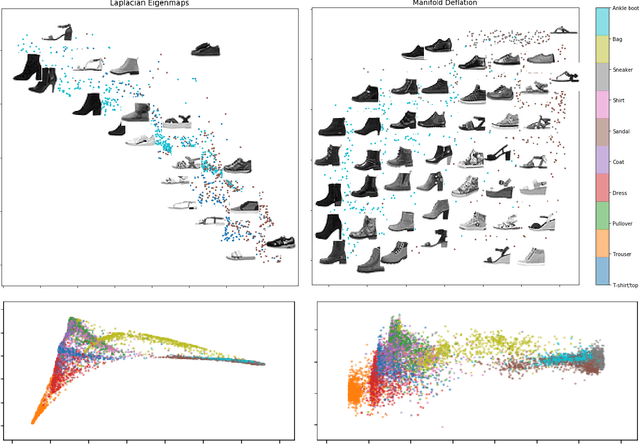
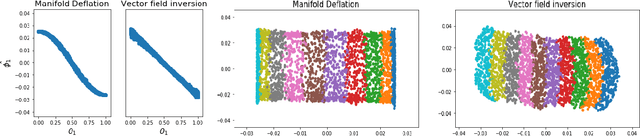
Nonlinear dimensionality reduction methods provide a valuable means to visualize and interpret high-dimensional data. However, many popular methods can fail dramatically, even on simple two-dimensional manifolds, due to problems such as vulnerability to noise, repeated eigendirections, holes in convex bodies, and boundary bias. We derive an embedding method for Riemannian manifolds that iteratively uses single-coordinate estimates to eliminate dimensions from an underlying differential operator, thus "deflating" it. These differential operators have been shown to characterize any local, spectral dimensionality reduction method. The key to our method is a novel, incremental tangent space estimator that incorporates global structure as coordinates are added. We prove its consistency when the coordinates converge to true coordinates. Empirically, we show our algorithm recovers novel and interesting embeddings on real-world and synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge