Evaluating the Impact of LLM-guided Reflection on Learning Outcomes with Interactive AI-Generated Educational Podcasts

This study examined whether embedding LLM-guided reflection prompts in an interactive AI-generated podcast improved learning and user experience compared to a version without prompts. Thirty-six undergraduates participated, and while learning outcomes were similar across conditions, reflection prompts reduced perceived attractiveness, highlighting a call for more research on reflective interactivity design.

Challenges Faced by Large Language Models in Solving Multi-Agent Flocking

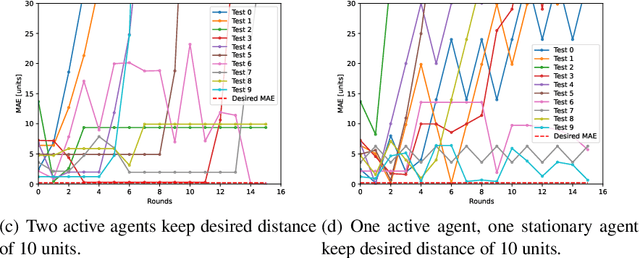
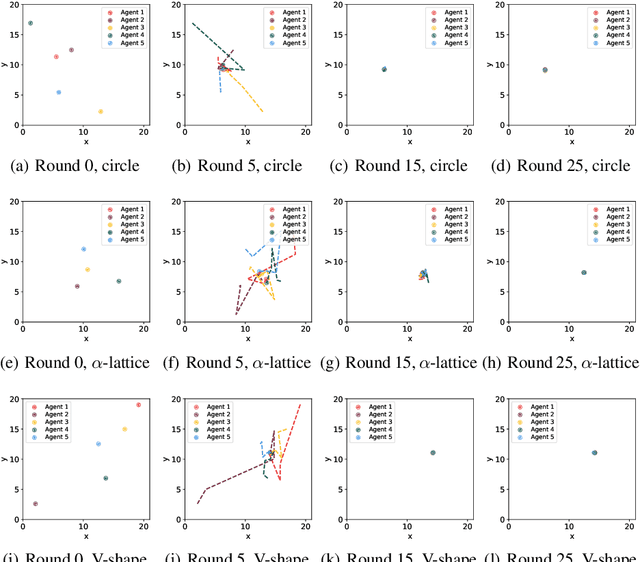
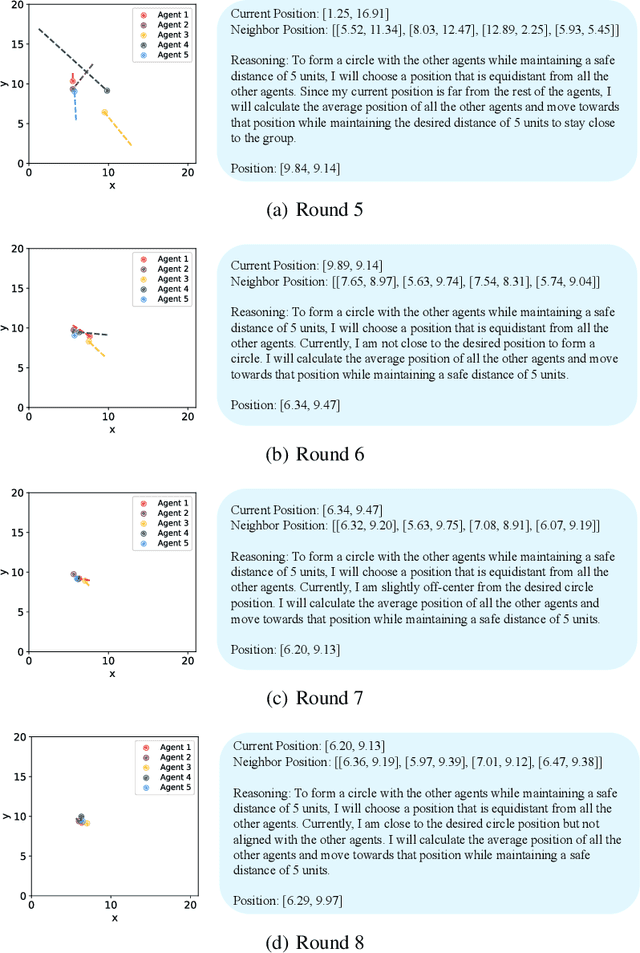
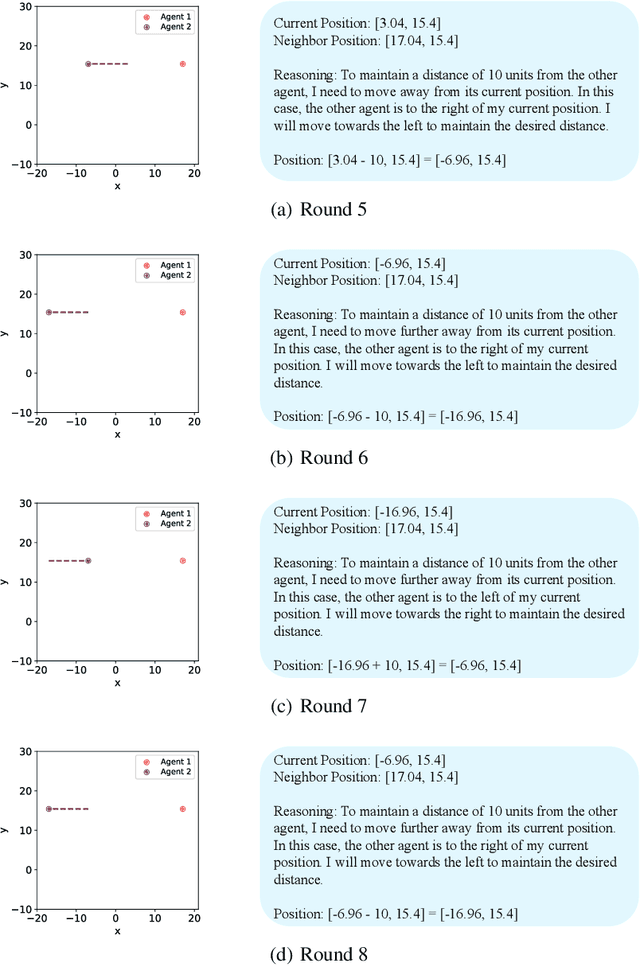
Flocking is a behavior where multiple agents in a system attempt to stay close to each other while avoiding collision and maintaining a desired formation. This is observed in the natural world and has applications in robotics, including natural disaster search and rescue, wild animal tracking, and perimeter surveillance and patrol. Recently, large language models (LLMs) have displayed an impressive ability to solve various collaboration tasks as individual decision-makers. Solving multi-agent flocking with LLMs would demonstrate their usefulness in situations requiring spatial and decentralized decision-making. Yet, when LLM-powered agents are tasked with implementing multi-agent flocking, they fall short of the desired behavior. After extensive testing, we find that agents with LLMs as individual decision-makers typically opt to converge on the average of their initial positions or diverge from each other. After breaking the problem down, we discover that LLMs cannot understand maintaining a shape or keeping a distance in a meaningful way. Solving multi-agent flocking with LLMs would enhance their ability to understand collaborative spatial reasoning and lay a foundation for addressing more complex multi-agent tasks. This paper discusses the challenges LLMs face in multi-agent flocking and suggests areas for future improvement and research.

Subspace clustering without knowing the number of clusters: A parameter free approach

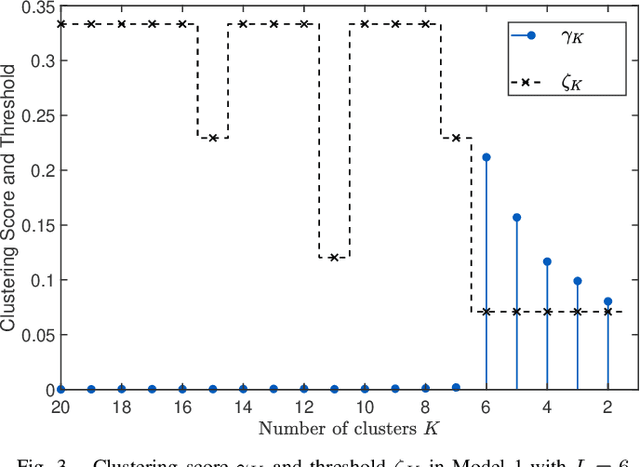
Subspace clustering, the task of clustering high dimensional data when the data points come from a union of subspaces is one of the fundamental tasks in unsupervised machine learning. Most of the existing algorithms for this task involves supplying prior information in form of a parameter, like the number of clusters, to the algorithm. In this work, a parameter free method for subspace clustering is proposed, where the data points are clustered on the basis of the difference in statistical distribution of the angles made by the data points within a subspace and those by points belonging to different subspaces. Given an initial coarse clustering, the proposed algorithm merges the clusters until a true clustering is obtained. This, unlike many existing methods, does not involve the use of an unknown parameter or tuning for one through cross validation. Also, a parameter free method for producing a coarse initial clustering is discussed, which makes the whole process of subspace clustering parameter free. The comparison of algorithm performance with the existing state of the art in synthetic and real data sets, shows the significance of the proposed method.

Structured and Unstructured Outlier Identification for Robust PCA: A Non iterative, Parameter free Algorithm

Robust PCA, the problem of PCA in the presence of outliers has been extensively investigated in the last few years. Here we focus on Robust PCA in the outlier model where each column of the data matrix is either an inlier or an outlier. Most of the existing methods for this model assumes either the knowledge of the dimension of the lower dimensional subspace or the fraction of outliers in the system. However in many applications knowledge of these parameters is not available. Motivated by this we propose a parameter free outlier identification method for robust PCA which a) does not require the knowledge of outlier fraction, b) does not require the knowledge of the dimension of the underlying subspace, c) is computationally simple and fast d) can handle structured and unstructured outliers. Further, analytical guarantees are derived for outlier identification and the performance of the algorithm is compared with the existing state of the art methods in both real and synthetic data for various outlier structures.

Fast, Parameter free Outlier Identification for Robust PCA

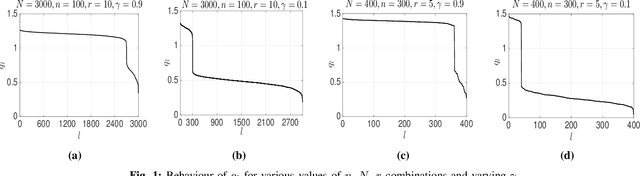
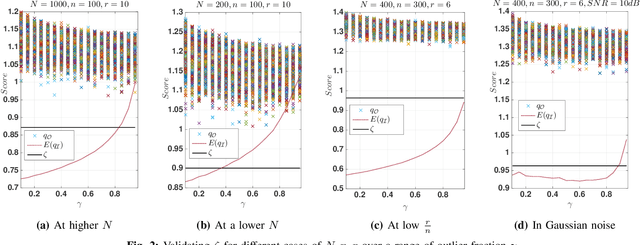
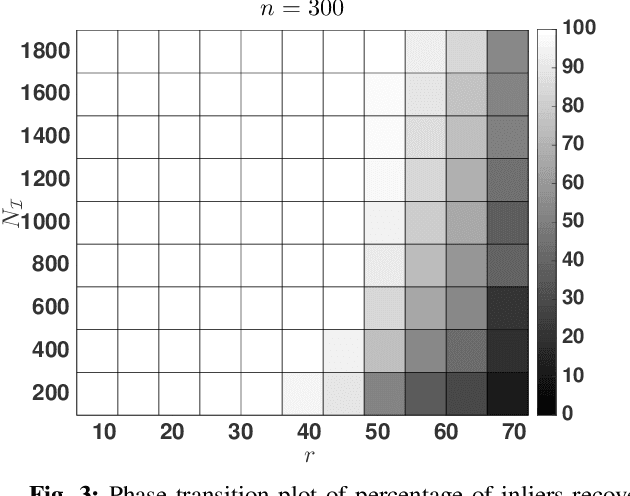
Robust PCA, the problem of PCA in the presence of outliers has been extensively investigated in the last few years. Here we focus on Robust PCA in the column sparse outlier model. The existing methods for column sparse outlier model assumes either the knowledge of the dimension of the lower dimensional subspace or the fraction of outliers in the system. However in many applications knowledge of these parameters is not available. Motivated by this we propose a parameter free outlier identification method for robust PCA which a) does not require the knowledge of outlier fraction, b) does not require the knowledge of the dimension of the underlying subspace, c) is computationally simple and fast. Further, analytical guarantees are derived for outlier identification and the performance of the algorithm is compared with the existing state of the art methods.