Introducing the Huber mechanism for differentially private low-rank matrix completion

Performing low-rank matrix completion with sensitive user data calls for privacy-preserving approaches. In this work, we propose a novel noise addition mechanism for preserving differential privacy where the noise distribution is inspired by Huber loss, a well-known loss function in robust statistics. The proposed Huber mechanism is evaluated against existing differential privacy mechanisms while solving the matrix completion problem using the Alternating Least Squares approach. We also propose using the Iteratively Re-Weighted Least Squares algorithm to complete low-rank matrices and study the performance of different noise mechanisms in both synthetic and real datasets. We prove that the proposed mechanism achieves {\epsilon}-differential privacy similar to the Laplace mechanism. Furthermore, empirical results indicate that the Huber mechanism outperforms Laplacian and Gaussian in some cases and is comparable, otherwise.

Subspace clustering without knowing the number of clusters: A parameter free approach

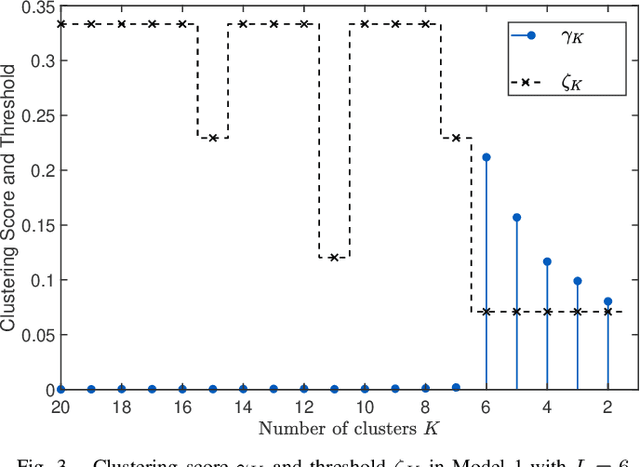
Subspace clustering, the task of clustering high dimensional data when the data points come from a union of subspaces is one of the fundamental tasks in unsupervised machine learning. Most of the existing algorithms for this task involves supplying prior information in form of a parameter, like the number of clusters, to the algorithm. In this work, a parameter free method for subspace clustering is proposed, where the data points are clustered on the basis of the difference in statistical distribution of the angles made by the data points within a subspace and those by points belonging to different subspaces. Given an initial coarse clustering, the proposed algorithm merges the clusters until a true clustering is obtained. This, unlike many existing methods, does not involve the use of an unknown parameter or tuning for one through cross validation. Also, a parameter free method for producing a coarse initial clustering is discussed, which makes the whole process of subspace clustering parameter free. The comparison of algorithm performance with the existing state of the art in synthetic and real data sets, shows the significance of the proposed method.