Online waveform selection for cognitive radar

Designing a cognitive radar system capable of adapting its parameters is challenging, particularly when tasked with tracking a ballistic missile throughout its entire flight. In this work, we focus on proposing adaptive algorithms that select waveform parameters in an online fashion. Our novelty lies in formulating the learning problem using domain knowledge derived from the characteristics of ballistic trajectories. We propose three reinforcement learning algorithms: bandwidth scaling, Q-learning, and Q-learning lookahead. These algorithms dynamically choose the bandwidth for each transmission based on received feedback. Through experiments on synthetically generated ballistic trajectories, we demonstrate that our proposed algorithms achieve the dual objectives of minimizing range error and maintaining continuous tracking without losing the target.

Probabilistic learning rate scheduler with provable convergence

Learning rate schedulers have shown great success in speeding up the convergence of learning algorithms in practice. However, their convergence to a minimum has not been proven theoretically. This difficulty mainly arises from the fact that, while traditional convergence analysis prescribes to monotonically decreasing (or constant) learning rates, schedulers opt for rates that often increase and decrease through the training epochs. In this work, we aim to bridge the gap by proposing a probabilistic learning rate scheduler (PLRS), that does not conform to the monotonically decreasing condition, with provable convergence guarantees. In addition to providing detailed convergence proofs, we also show experimental results where the proposed PLRS performs competitively as other state-of-the-art learning rate schedulers across a variety of datasets and architectures.

Introducing the Huber mechanism for differentially private low-rank matrix completion

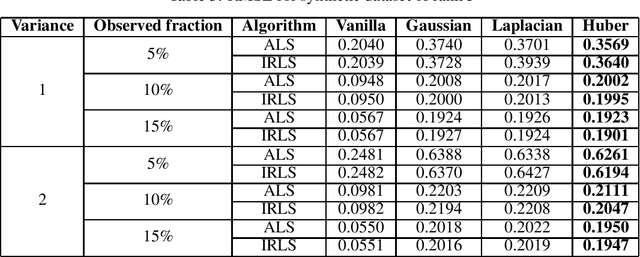
Performing low-rank matrix completion with sensitive user data calls for privacy-preserving approaches. In this work, we propose a novel noise addition mechanism for preserving differential privacy where the noise distribution is inspired by Huber loss, a well-known loss function in robust statistics. The proposed Huber mechanism is evaluated against existing differential privacy mechanisms while solving the matrix completion problem using the Alternating Least Squares approach. We also propose using the Iteratively Re-Weighted Least Squares algorithm to complete low-rank matrices and study the performance of different noise mechanisms in both synthetic and real datasets. We prove that the proposed mechanism achieves {\epsilon}-differential privacy similar to the Laplace mechanism. Furthermore, empirical results indicate that the Huber mechanism outperforms Laplacian and Gaussian in some cases and is comparable, otherwise.

The robust way to stack and bag: the local Lipschitz way

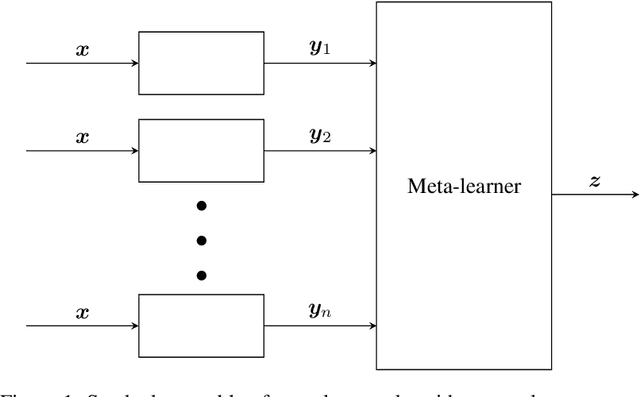
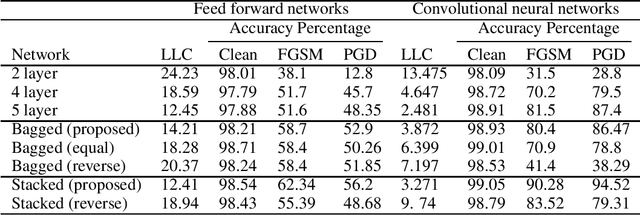
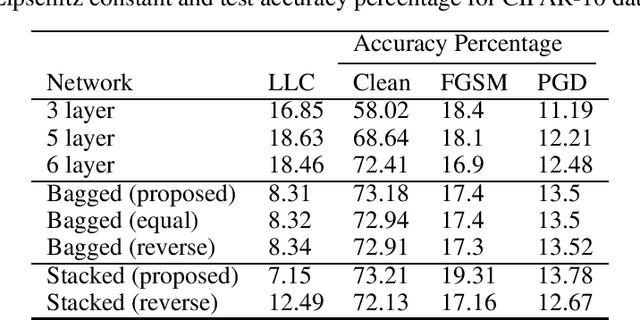
Recent research has established that the local Lipschitz constant of a neural network directly influences its adversarial robustness. We exploit this relationship to construct an ensemble of neural networks which not only improves the accuracy, but also provides increased adversarial robustness. The local Lipschitz constants for two different ensemble methods - bagging and stacking - are derived and the architectures best suited for ensuring adversarial robustness are deduced. The proposed ensemble architectures are tested on MNIST and CIFAR-10 datasets in the presence of white-box attacks, FGSM and PGD. The proposed architecture is found to be more robust than a) a single network and b) traditional ensemble methods.

How to boost autoencoders?

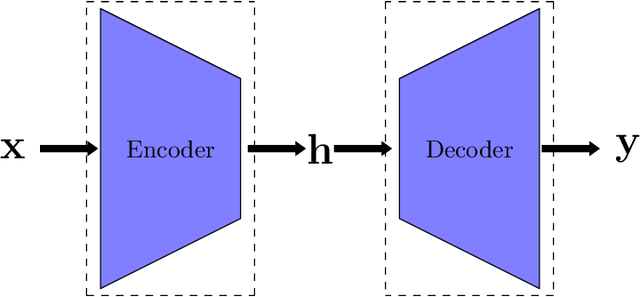
Autoencoders are a category of neural networks with applications in numerous domains and hence, improvement of their performance is gaining substantial interest from the machine learning community. Ensemble methods, such as boosting, are often adopted to enhance the performance of regular neural networks. In this work, we discuss the challenges associated with boosting autoencoders and propose a framework to overcome them. The proposed method ensures that the advantages of boosting are realized when either output (encoded or reconstructed) is used. The usefulness of the boosted ensemble is demonstrated in two applications that widely employ autoencoders: anomaly detection and clustering.

On the Differentially Private Nature of Perturbed Gradient Descent

We consider the problem of empirical risk minimization given a database, using the gradient descent algorithm. We note that the function to be optimized may be non-convex, consisting of saddle points which impede the convergence of the algorithm. A perturbed gradient descent algorithm is typically employed to escape these saddle points. We show that this algorithm, that perturbs the gradient, inherently preserves the privacy of the data. We then employ the differential privacy framework to quantify the privacy hence achieved. We also analyze the change in privacy with varying parameters such as problem dimension and the distance between the databases.

Tune smarter not harder: A principled approach to tuning learning rates for shallow nets

Effective hyper-parameter tuning is essential to guarantee the performance that neural networks have come to be known for. In this work, a principled approach to choosing the learning rate is proposed for shallow feedforward neural networks. We associate the learning rate with the gradient Lipschitz constant of the objective to be minimized while training. An upper bound on the mentioned constant is derived and a search algorithm, which always results in non-divergent traces, is proposed to exploit the derived bound. It is shown through simulations that the proposed search method significantly outperforms the existing tuning methods such as Tree Parzen Estimators (TPE). The proposed method is applied to two different existing applications, namely, channel estimation in a wireless communication system and prediction of the exchange currency rates, and it is shown to pick better learning rates than the existing methods using the same or lesser compute power.

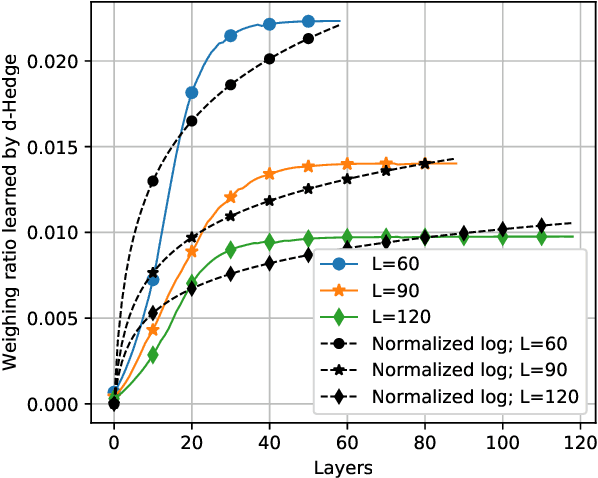
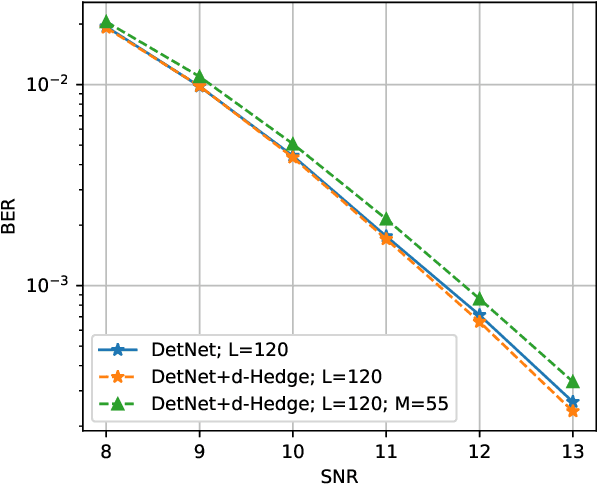
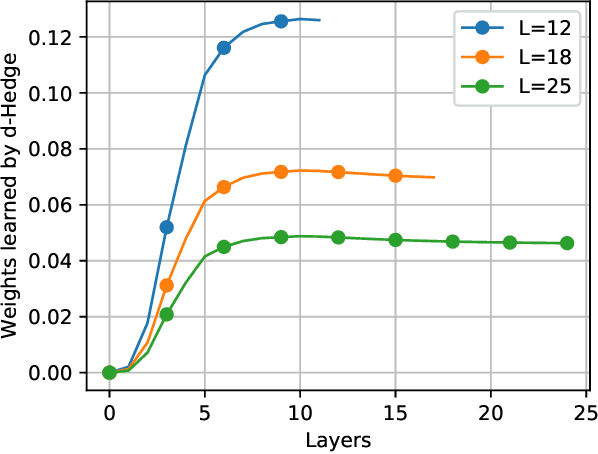
What is the optimal depth for deep-unfolding architectures at deployment?

Recently, many iterative algorithms proposed for various applications such as compressed sensing, MIMO Detection, etc. have been unfolded and presented as deep networks; these networks are shown to produce better results than the algorithms in their iterative forms. However, deep networks are highly sensitive to the hyperparameters chosen. Especially for a deep unfolded network, using more layers may lead to redundancy and hence, excessive computation during deployment. In this work, we consider the problem of determining the optimal number of layers required for such unfolded architectures. We propose a method that treats the networks as experts and measures the relative importance of the expertise provided by layers using a variant of the popular Hedge algorithm. Based on the importance of the different layers, we determine the optimal layers required for deployment. We study the effectiveness of this method by applying it to two recent and popular deep-unfolding architectures, namely DetNet and TISTANet.

Concavifiability and convergence: necessary and sufficient conditions for gradient descent analysis

Convergence of the gradient descent algorithm has been attracting renewed interest due to its utility in deep learning applications. Even as multiple variants of gradient descent were proposed, the assumption that the gradient of the objective is Lipschitz continuous remained an integral part of the analysis until recently. In this work, we look at convergence analysis by focusing on a property that we term as concavifiability, instead of Lipschitz continuity of gradients. We show that concavifiability is a necessary and sufficient condition to satisfy the upper quadratic approximation which is key in proving that the objective function decreases after every gradient descent update. We also show that any gradient Lipschitz function satisfies concavifiability. A constant known as the concavifier analogous to the gradient Lipschitz constant is derived which is indicative of the optimal step size. As an application, we demonstrate the utility of finding the concavifier the in convergence of gradient descent through an example inspired by neural networks. We derive bounds on the concavifier to obtain a fixed step size for a single hidden layer ReLU network.

A Non-parametric Multi-stage Learning Framework for Cognitive Spectrum Access in IoT Networks

Given the increasing number of devices that is going to get connected to wireless networks with the advent of Internet of Things, spectrum scarcity will present a major challenge. Application of opportunistic spectrum access mechanisms to IoT networks will become increasingly important to solve this. In this paper, we present a cognitive radio network architecture which uses multi-stage online learning techniques for spectrum assignment to devices, with the aim of improving the throughput and energy efficiency of the IoT devices. In the first stage, we use an AI technique to learn the quality of a user-channel pairing. The next stage utilizes a non-parametric Bayesian learning algorithm to estimate the Primary User OFF time in each channel. The third stage augments the Bayesian learner with implicit exploration to accelerate the learning procedure. The proposed method leads to significant improvement in throughput and energy efficiency of the IoT devices while keeping the interference to the primary users minimal. We provide comprehensive empirical validation of the method with other learning based approaches.