On Nonlinear Dimensionality Reduction, Linear Smoothing and Autoencoding
Paper and Code
Mar 06, 2018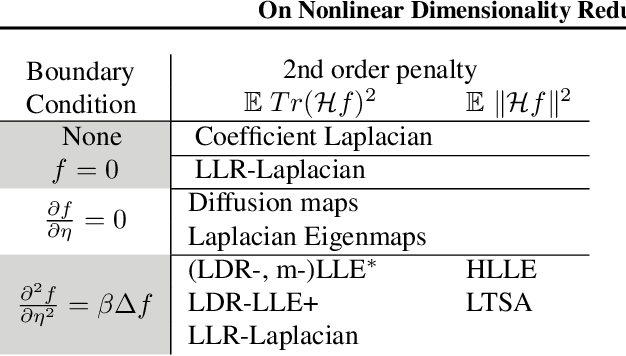
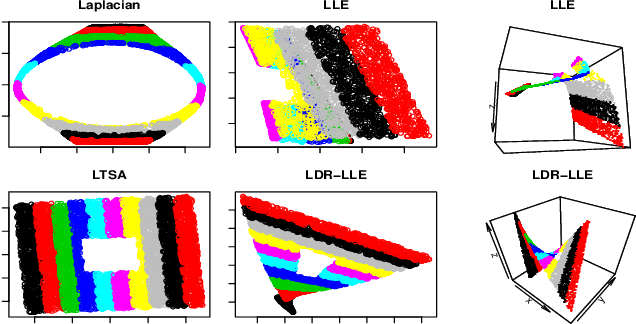

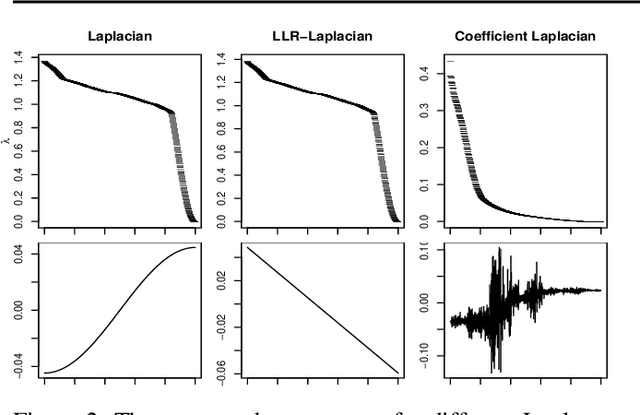
We develop theory for nonlinear dimensionality reduction (NLDR). A number of NLDR methods have been developed, but there is limited understanding of how these methods work and the relationships between them. There is limited basis for using existing NLDR theory for deriving new algorithms. We provide a novel framework for analysis of NLDR via a connection to the statistical theory of linear smoothers. This allows us to both understand existing methods and derive new ones. We use this connection to smoothing to show that asymptotically, existing NLDR methods correspond to discrete approximations of the solutions of sets of differential equations given a boundary condition. In particular, we can characterize many existing methods in terms of just three limiting differential operators and boundary conditions. Our theory also provides a way to assert that one method is preferable to another; indeed, we show Local Tangent Space Alignment is superior within a class of methods that assume a global coordinate chart defines an isometric embedding of the manifold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge