Fair and Welfare-Efficient Constrained Multi-matchings under Uncertainty

We study fair allocation of constrained resources, where a market designer optimizes overall welfare while maintaining group fairness. In many large-scale settings, utilities are not known in advance, but are instead observed after realizing the allocation. We therefore estimate agent utilities using machine learning. Optimizing over estimates requires trading-off between mean utilities and their predictive variances. We discuss these trade-offs under two paradigms for preference modeling -- in the stochastic optimization regime, the market designer has access to a probability distribution over utilities, and in the robust optimization regime they have access to an uncertainty set containing the true utilities with high probability. We discuss utilitarian and egalitarian welfare objectives, and we explore how to optimize for them under stochastic and robust paradigms. We demonstrate the efficacy of our approaches on three publicly available conference reviewer assignment datasets. The approaches presented enable scalable constrained resource allocation under uncertainty for many combinations of objectives and preference models.

Percentile Criterion Optimization in Offline Reinforcement Learning

In reinforcement learning, robust policies for high-stakes decision-making problems with limited data are usually computed by optimizing the \emph{percentile criterion}. The percentile criterion is approximately solved by constructing an \emph{ambiguity set} that contains the true model with high probability and optimizing the policy for the worst model in the set. Since the percentile criterion is non-convex, constructing ambiguity sets is often challenging. Existing work uses \emph{Bayesian credible regions} as ambiguity sets, but they are often unnecessarily large and result in learning overly conservative policies. To overcome these shortcomings, we propose a novel Value-at-Risk based dynamic programming algorithm to optimize the percentile criterion without explicitly constructing any ambiguity sets. Our theoretical and empirical results show that our algorithm implicitly constructs much smaller ambiguity sets and learns less conservative robust policies.

To Pool or Not To Pool: Analyzing the Regularizing Effects of Group-Fair Training on Shared Models

In fair machine learning, one source of performance disparities between groups is over-fitting to groups with relatively few training samples. We derive group-specific bounds on the generalization error of welfare-centric fair machine learning that benefit from the larger sample size of the majority group. We do this by considering group-specific Rademacher averages over a restricted hypothesis class, which contains the family of models likely to perform well with respect to a fair learning objective (e.g., a power-mean). Our simulations demonstrate these bounds improve over a naive method, as expected by theory, with particularly significant improvement for smaller group sizes.

Dividing Good and Better Items Among Agents with Submodular Valuations

We study the problem of fairly allocating a set of indivisible goods among agents with bivalued submodular valuations -- each good provides a marginal gain of either $a$ or $b$ ($a < b$) and goods have decreasing marginal gains. This is a natural generalization of two well-studied valuation classes -- bivalued additive valuations and binary submodular valuations. We present a simple sequential algorithmic framework, based on the recently introduced Yankee Swap mechanism, that can be adapted to compute a variety of solution concepts, including leximin, max Nash welfare (MNW) and $p$-mean welfare maximizing allocations when $a$ divides $b$. This result is complemented by an existing result on the computational intractability of leximin and MNW allocations when $a$ does not divide $b$. We further examine leximin and MNW allocations with respect to two well-known properties -- envy freeness and the maximin share guarantee. On envy freeness, we show that neither the leximin nor the MNW allocation is guaranteed to be envy free up to one good (EF1). This is surprising since for the simpler classes of bivalued additive valuations and binary submodular valuations, MNW allocations are known to be envy free up to any good (EFX). On the maximin share guarantee, we show that MNW and leximin allocations guarantee each agent $\frac14$ and $\frac{a}{b+3a}$ of their maximin share respectively when $a$ divides $b$. This fraction improves to $\frac13$ and $\frac{a}{b+2a}$ respectively when agents have bivalued additive valuations.

Fast Doubly-Adaptive MCMC to Estimate the Gibbs Partition Function with Weak Mixing Time Bounds

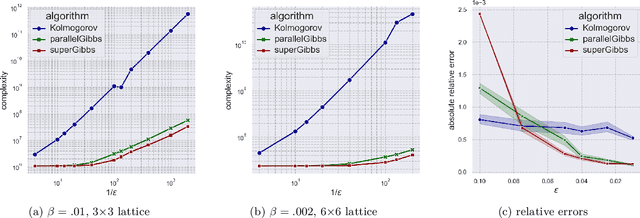
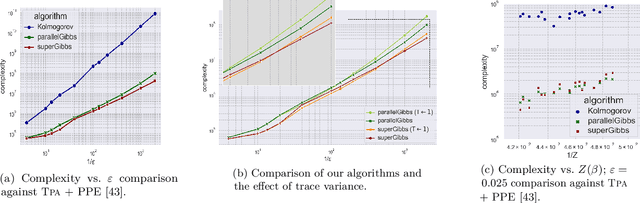
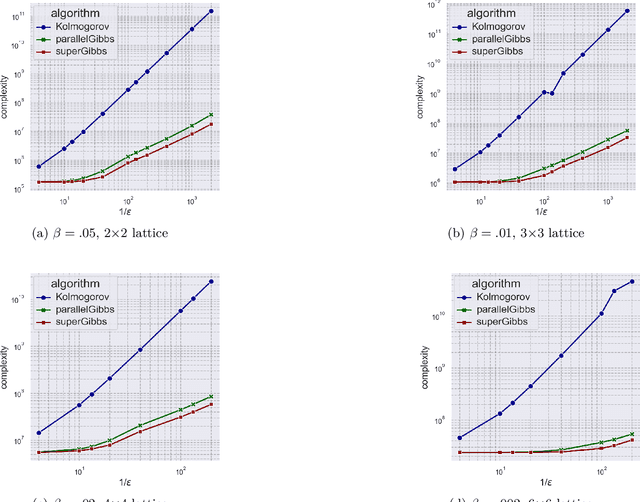
We present a novel method for reducing the computational complexity of rigorously estimating the partition functions (normalizing constants) of Gibbs (Boltzmann) distributions, which arise ubiquitously in probabilistic graphical models. A major obstacle to practical applications of Gibbs distributions is the need to estimate their partition functions. The state of the art in addressing this problem is multi-stage algorithms, which consist of a cooling schedule, and a mean estimator in each step of the schedule. While the cooling schedule in these algorithms is adaptive, the mean estimation computations use MCMC as a black-box to draw approximate samples. We develop a doubly adaptive approach, combining the adaptive cooling schedule with an adaptive MCMC mean estimator, whose number of Markov chain steps adapts dynamically to the underlying chain. Through rigorous theoretical analysis, we prove that our method outperforms the state of the art algorithms in several factors: (1) The computational complexity of our method is smaller; (2) Our method is less sensitive to loose bounds on mixing times, an inherent component in these algorithms; and (3) The improvement obtained by our method is particularly significant in the most challenging regime of high-precision estimation. We demonstrate the advantage of our method in experiments run on classic factor graphs, such as voting models and Ising models.

An Axiomatic Theory of Provably-Fair Welfare-Centric Machine Learning

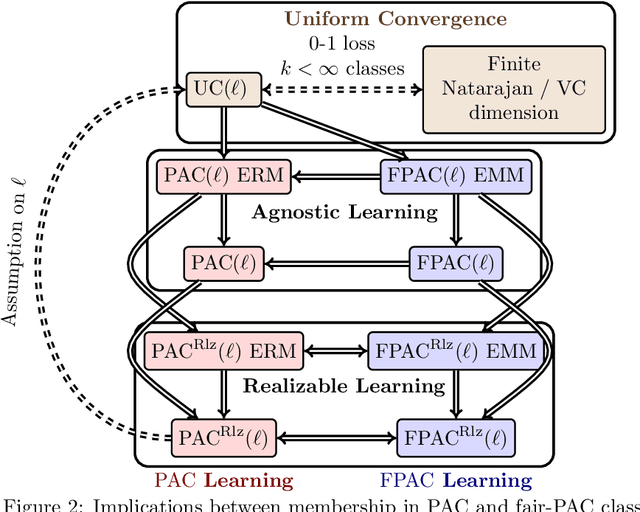
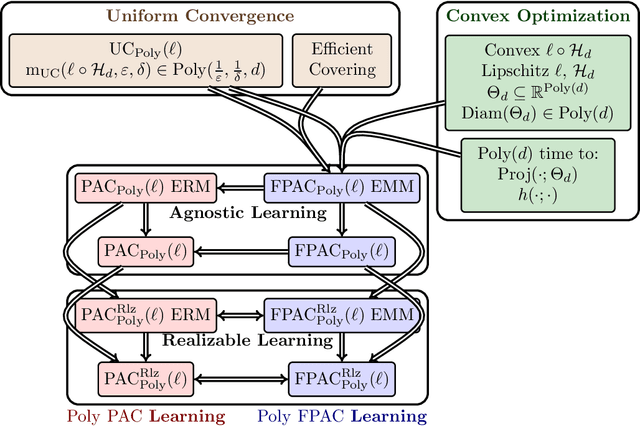
We address an inherent difficulty in welfare-theoretic fair machine learning, proposing an equivalently-axiomatically justified alternative, and studying the resulting computational and statistical learning questions. Welfare metrics quantify overall wellbeing across a population of one or more groups, and welfare-based objectives and constraints have recently been proposed to incentivize fair machine learning methods to produce satisfactory solutions that consider the diverse needs of multiple groups. Unfortunately, many machine-learning problems are more naturally cast as loss minimization, rather than utility maximization tasks, which complicates direct application of welfare-centric methods to fair-ML tasks. In this work, we define a complementary measure, termed malfare, measuring overall societal harm (rather than wellbeing), with axiomatic justification via the standard axioms of cardinal welfare. We then cast fair machine learning as a direct malfare minimization problem, where a group's malfare is their risk (expected loss). Surprisingly, the axioms of cardinal welfare (malfare) dictate that this is not equivalent to simply defining utility as negative loss. Building upon these concepts, we define fair-PAC learning, where a fair PAC-learner is an algorithm that learns an $\varepsilon$-$\delta$ malfare-optimal model with bounded sample complexity, for any data distribution, and for any malfare concept. We show broad conditions under which, with appropriate modifications, many standard PAC-learners may be converted to fair-PAC learners. This places fair-PAC learning on firm theoretical ground, as it yields statistical, and in some cases computational, efficiency guarantees for many well-studied machine-learning models, and is also practically relevant, as it democratizes fair ML by providing concrete training algorithms and rigorous generalization guarantees for these models.

MCRapper: Monte-Carlo Rademacher Averages for Poset Families and Approximate Pattern Mining

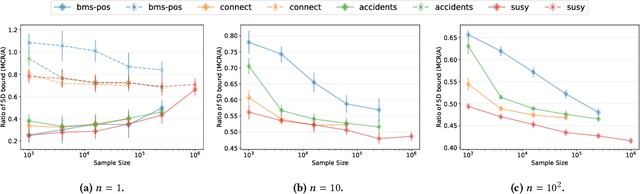
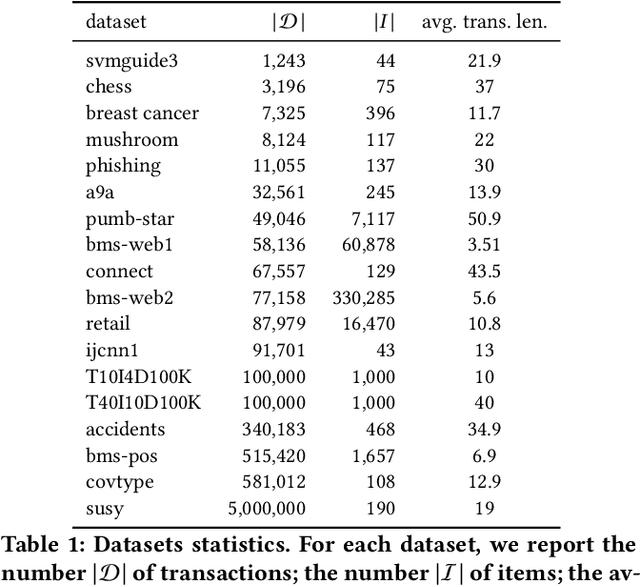
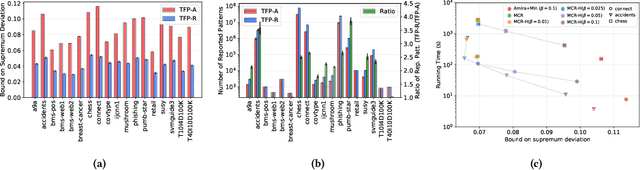
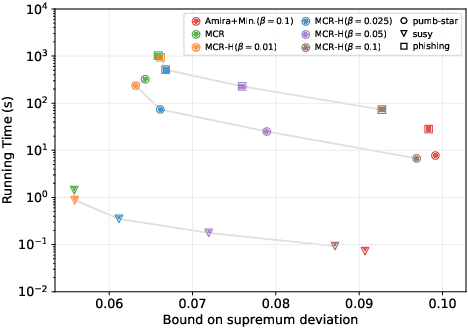
We present MCRapper, an algorithm for efficient computation of Monte-Carlo Empirical Rademacher Averages (MCERA) for families of functions exhibiting poset (e.g., lattice) structure, such as those that arise in many pattern mining tasks. The MCERA allows us to compute upper bounds to the maximum deviation of sample means from their expectations, thus it can be used to find both statistically-significant functions (i.e., patterns) when the available data is seen as a sample from an unknown distribution, and approximations of collections of high-expectation functions (e.g., frequent patterns) when the available data is a small sample from a large dataset. This feature is a strong improvement over previously proposed solutions that could only achieve one of the two. MCRapper uses upper bounds to the discrepancy of the functions to efficiently explore and prune the search space, a technique borrowed from pattern mining itself. To show the practical use of MCRapper, we employ it to develop an algorithm TFP-R for the task of True Frequent Pattern (TFP) mining. TFP-R gives guarantees on the probability of including any false positives (precision) and exhibits higher statistical power (recall) than existing methods offering the same guarantees. We evaluate MCRapper and TFP-R and show that they outperform the state-of-the-art for their respective tasks.

Uniform Convergence Bounds for Codec Selection

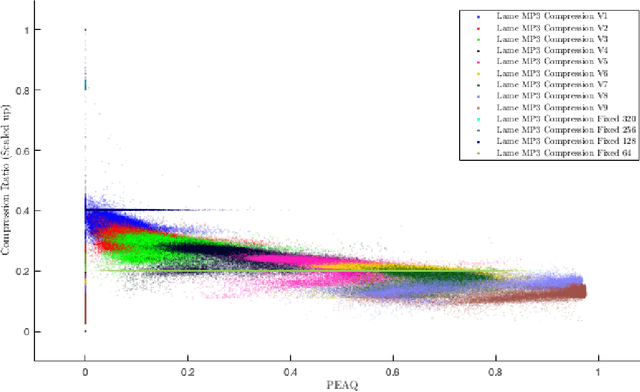
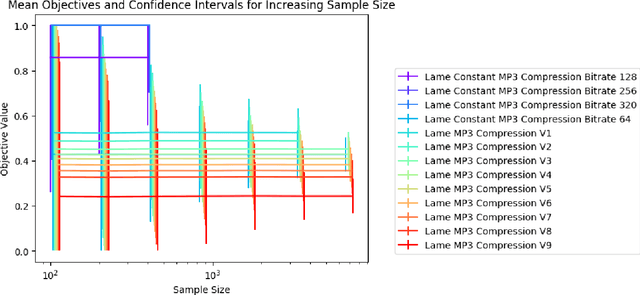
We frame the problem of selecting an optimal audio encoding scheme as a supervised learning task. Through uniform convergence theory, we guarantee approximately optimal codec selection while controlling for selection bias. We present rigorous statistical guarantees for the codec selection problem that hold for arbitrary distributions over audio sequences and for arbitrary quality metrics. Our techniques can thus balance sound quality and compression ratio, and use audio samples from the distribution to select a codec that performs well on that particular type of data. The applications of our technique are immense, as it can be used to optimize for quality and bandwidth usage of streaming and other digital media, while significantly outperforming approaches that apply a fixed codec to all data sources.