An Adaptive Method for Weak Supervision with Drifting Data

We introduce an adaptive method with formal quality guarantees for weak supervision in a non-stationary setting. Our goal is to infer the unknown labels of a sequence of data by using weak supervision sources that provide independent noisy signals of the correct classification for each data point. This setting includes crowdsourcing and programmatic weak supervision. We focus on the non-stationary case, where the accuracy of the weak supervision sources can drift over time, e.g., because of changes in the underlying data distribution. Due to the drift, older data could provide misleading information to infer the label of the current data point. Previous work relied on a priori assumptions on the magnitude of the drift to decide how much data to use from the past. Comparatively, our algorithm does not require any assumptions on the drift, and it adapts based on the input. In particular, at each step, our algorithm guarantees an estimation of the current accuracies of the weak supervision sources over a window of past observations that minimizes a trade-off between the error due to the variance of the estimation and the error due to the drift. Experiments on synthetic and real-world labelers show that our approach indeed adapts to the drift. Unlike fixed-window-size strategies, it dynamically chooses a window size that allows it to consistently maintain good performance.

An Adaptive Algorithm for Learning with Unknown Distribution Drift

We develop and analyze a general technique for learning with an unknown distribution drift. Given a sequence of independent observations from the last $T$ steps of a drifting distribution, our algorithm agnostically learns a family of functions with respect to the current distribution at time $T$. Unlike previous work, our technique does not require prior knowledge about the magnitude of the drift. Instead, the algorithm adapts to the sample data. Without explicitly estimating the drift, the algorithm learns a family of functions with almost the same error as a learning algorithm that knows the magnitude of the drift in advance. Furthermore, since our algorithm adapts to the data, it can guarantee a better learning error than an algorithm that relies on loose bounds on the drift.

Nonparametric Density Estimation under Distribution Drift

We study nonparametric density estimation in non-stationary drift settings. Given a sequence of independent samples taken from a distribution that gradually changes in time, the goal is to compute the best estimate for the current distribution. We prove tight minimax risk bounds for both discrete and continuous smooth densities, where the minimum is over all possible estimates and the maximum is over all possible distributions that satisfy the drift constraints. Our technique handles a broad class of drift models, and generalizes previous results on agnostic learning under drift.

Tight Lower Bounds on Worst-Case Guarantees for Zero-Shot Learning with Attributes

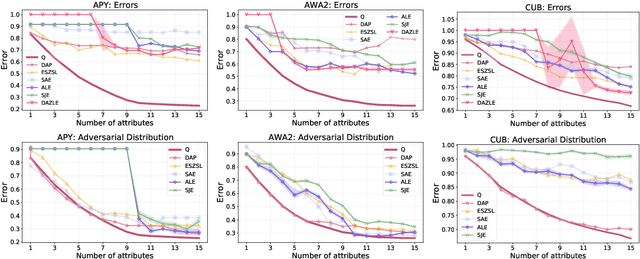
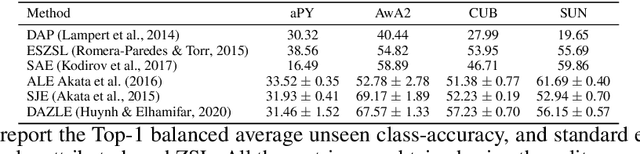
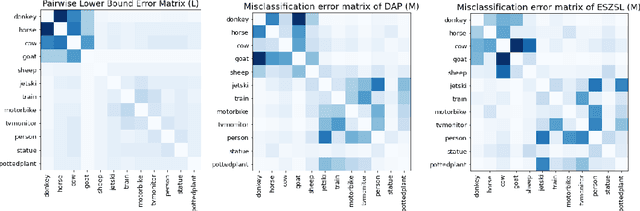
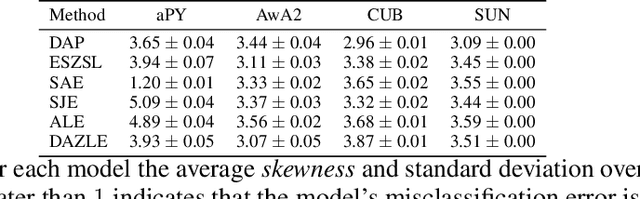
We develop a rigorous mathematical analysis of zero-shot learning with attributes. In this setting, the goal is to label novel classes with no training data, only detectors for attributes and a description of how those attributes are correlated with the target classes, called the class-attribute matrix. We develop the first non-trivial lower bound on the worst-case error of the best map from attributes to classes for this setting, even with perfect attribute detectors. The lower bound characterizes the theoretical intrinsic difficulty of the zero-shot problem based on the available information -- the class-attribute matrix -- and the bound is practically computable from it. Our lower bound is tight, as we show that we can always find a randomized map from attributes to classes whose expected error is upper bounded by the value of the lower bound. We show that our analysis can be predictive of how standard zero-shot methods behave in practice, including which classes will likely be confused with others.

Fast Doubly-Adaptive MCMC to Estimate the Gibbs Partition Function with Weak Mixing Time Bounds

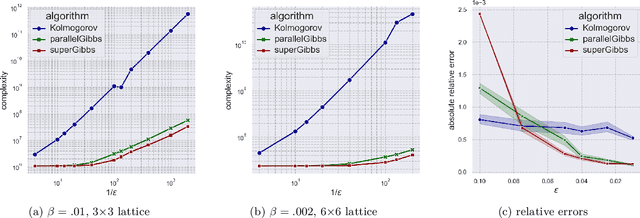
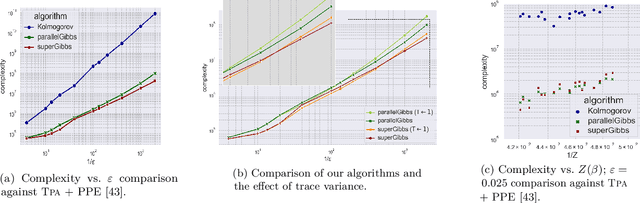
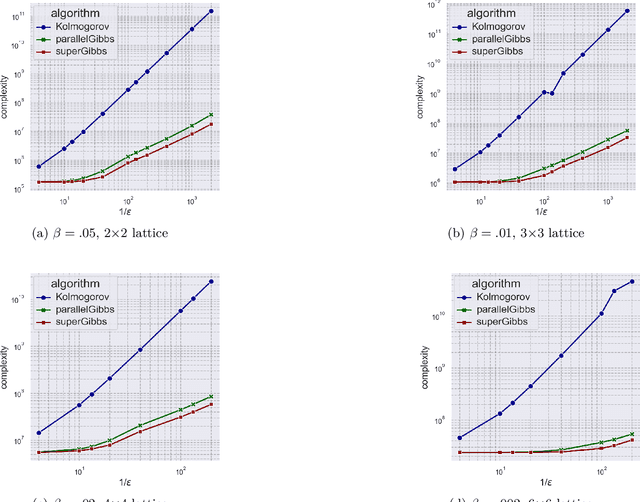
We present a novel method for reducing the computational complexity of rigorously estimating the partition functions (normalizing constants) of Gibbs (Boltzmann) distributions, which arise ubiquitously in probabilistic graphical models. A major obstacle to practical applications of Gibbs distributions is the need to estimate their partition functions. The state of the art in addressing this problem is multi-stage algorithms, which consist of a cooling schedule, and a mean estimator in each step of the schedule. While the cooling schedule in these algorithms is adaptive, the mean estimation computations use MCMC as a black-box to draw approximate samples. We develop a doubly adaptive approach, combining the adaptive cooling schedule with an adaptive MCMC mean estimator, whose number of Markov chain steps adapts dynamically to the underlying chain. Through rigorous theoretical analysis, we prove that our method outperforms the state of the art algorithms in several factors: (1) The computational complexity of our method is smaller; (2) Our method is less sensitive to loose bounds on mixing times, an inherent component in these algorithms; and (3) The improvement obtained by our method is particularly significant in the most challenging regime of high-precision estimation. We demonstrate the advantage of our method in experiments run on classic factor graphs, such as voting models and Ising models.

A Rademacher Complexity Based Method fo rControlling Power and Confidence Level in Adaptive Statistical Analysis

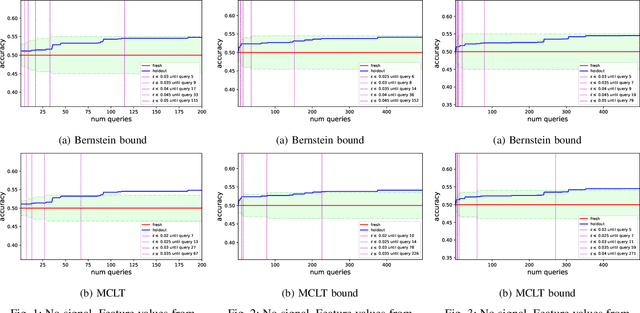
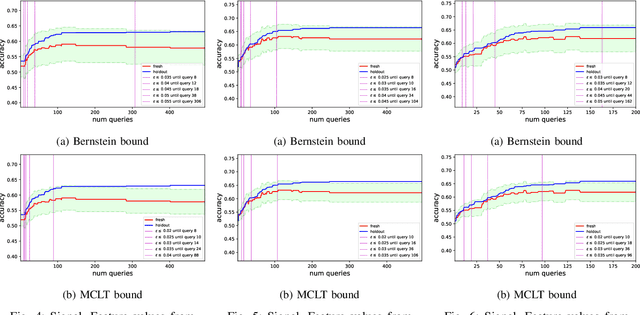
While standard statistical inference techniques and machine learning generalization bounds assume that tests are run on data selected independently of the hypotheses, practical data analysis and machine learning are usually iterative and adaptive processes where the same holdout data is often used for testing a sequence of hypotheses (or models), which may each depend on the outcome of the previous tests on the same data. In this work, we present RadaBound a rigorous, efficient and practical procedure for controlling the generalization error when using a holdout sample for multiple adaptive testing. Our solution is based on a new application of the Rademacher Complexity generalization bounds, adapted to dependent tests. We demonstrate the statistical power and practicality of our method through extensive simulations and comparisons to alternative approaches.

Uniform Convergence Bounds for Codec Selection

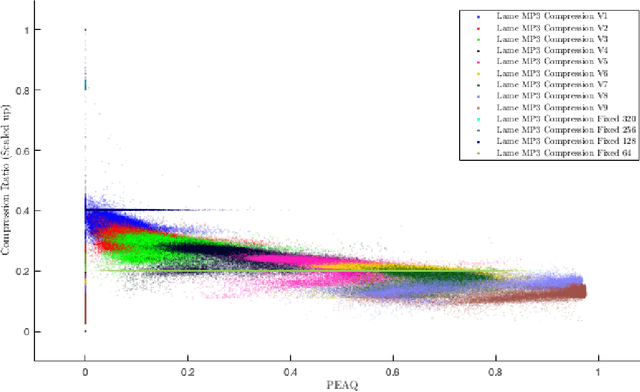
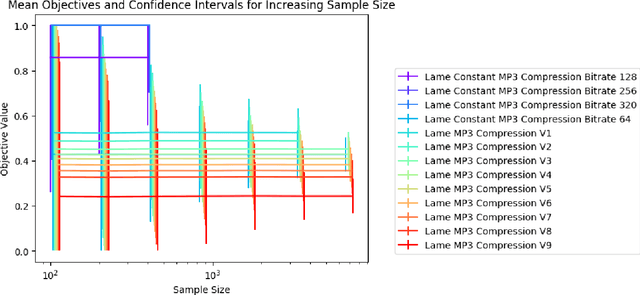
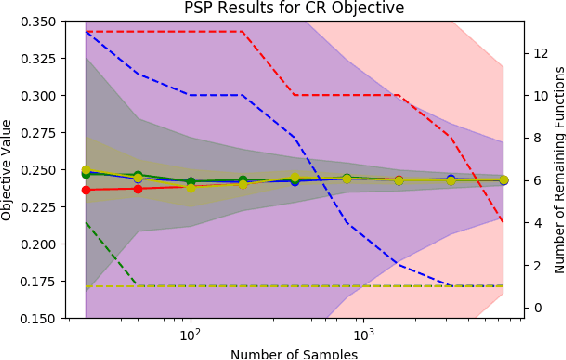
We frame the problem of selecting an optimal audio encoding scheme as a supervised learning task. Through uniform convergence theory, we guarantee approximately optimal codec selection while controlling for selection bias. We present rigorous statistical guarantees for the codec selection problem that hold for arbitrary distributions over audio sequences and for arbitrary quality metrics. Our techniques can thus balance sound quality and compression ratio, and use audio samples from the distribution to select a codec that performs well on that particular type of data. The applications of our technique are immense, as it can be used to optimize for quality and bandwidth usage of streaming and other digital media, while significantly outperforming approaches that apply a fixed codec to all data sources.

Unknown Examples & Machine Learning Model Generalization

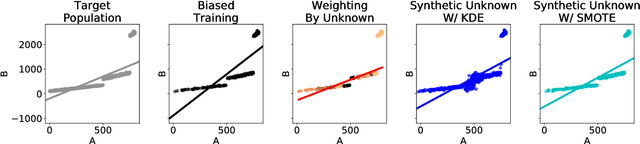
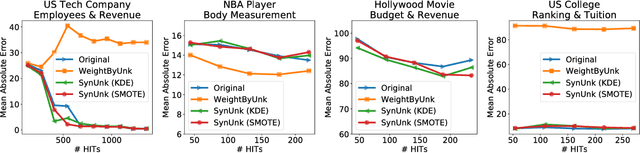
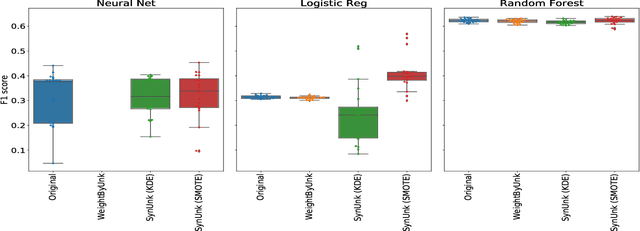
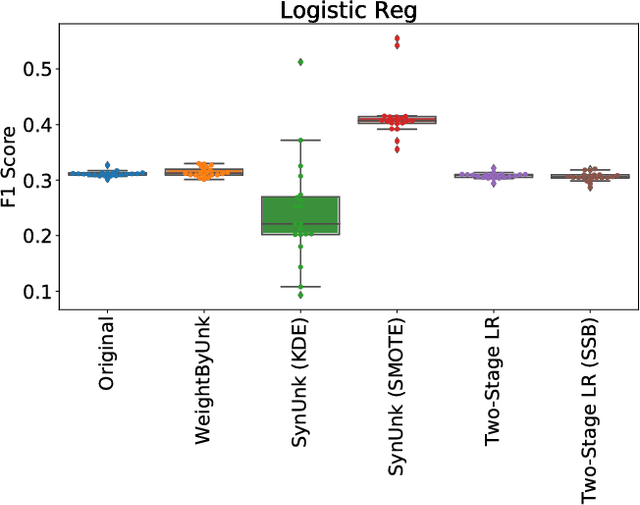
Over the past decades, researchers and ML practitioners have come up with better and better ways to build, understand and improve the quality of ML models, but mostly under the key assumption that the training data is distributed identically to the testing data. In many real-world applications, however, some potential training examples are unknown to the modeler, due to sample selection bias or, more generally, covariate shift, i.e., a distribution shift between the training and deployment stage. The resulting discrepancy between training and testing distributions leads to poor generalization performance of the ML model and hence biased predictions. We provide novel algorithms that estimate the number and properties of these unknown training examples---unknown unknowns. This information can then be used to correct the training set, prior to seeing any test data. The key idea is to combine species-estimation techniques with data-driven methods for estimating the feature values for the unknown unknowns. Experiments on a variety of ML models and datasets indicate that taking the unknown examples into account can yield a more robust ML model that generalizes better.

Machine Learning in High Energy Physics Community White Paper

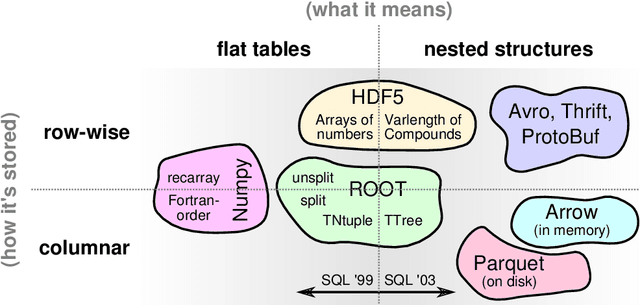
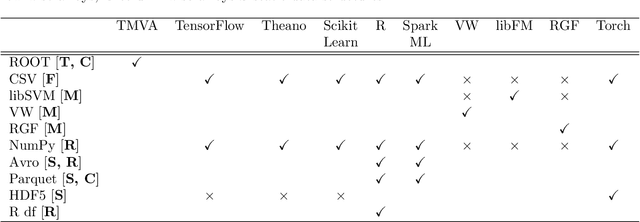
Machine learning is an important research area in particle physics, beginning with applications to high-level physics analysis in the 1990s and 2000s, followed by an explosion of applications in particle and event identification and reconstruction in the 2010s. In this document we discuss promising future research and development areas in machine learning in particle physics with a roadmap for their implementation, software and hardware resource requirements, collaborative initiatives with the data science community, academia and industry, and training the particle physics community in data science. The main objective of the document is to connect and motivate these areas of research and development with the physics drivers of the High-Luminosity Large Hadron Collider and future neutrino experiments and identify the resource needs for their implementation. Additionally we identify areas where collaboration with external communities will be of great benefit.

Bandits and Experts in Metric Spaces

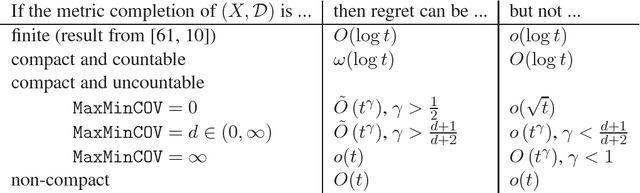
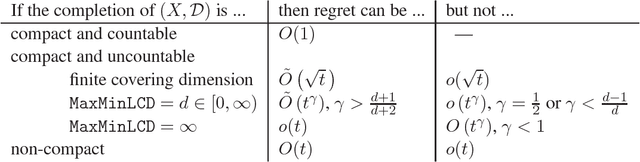
In a multi-armed bandit problem, an online algorithm chooses from a set of strategies in a sequence of trials so as to maximize the total payoff of the chosen strategies. While the performance of bandit algorithms with a small finite strategy set is quite well understood, bandit problems with large strategy sets are still a topic of very active investigation, motivated by practical applications such as online auctions and web advertisement. The goal of such research is to identify broad and natural classes of strategy sets and payoff functions which enable the design of efficient solutions. In this work we study a very general setting for the multi-armed bandit problem in which the strategies form a metric space, and the payoff function satisfies a Lipschitz condition with respect to the metric. We refer to this problem as the "Lipschitz MAB problem". We present a solution for the multi-armed bandit problem in this setting. That is, for every metric space we define an isometry invariant which bounds from below the performance of Lipschitz MAB algorithms for this metric space, and we present an algorithm which comes arbitrarily close to meeting this bound. Furthermore, our technique gives even better results for benign payoff functions. We also address the full-feedback ("best expert") version of the problem, where after every round the payoffs from all arms are revealed.