MCRapper: Monte-Carlo Rademacher Averages for Poset Families and Approximate Pattern Mining

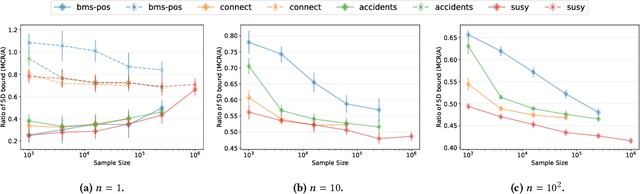
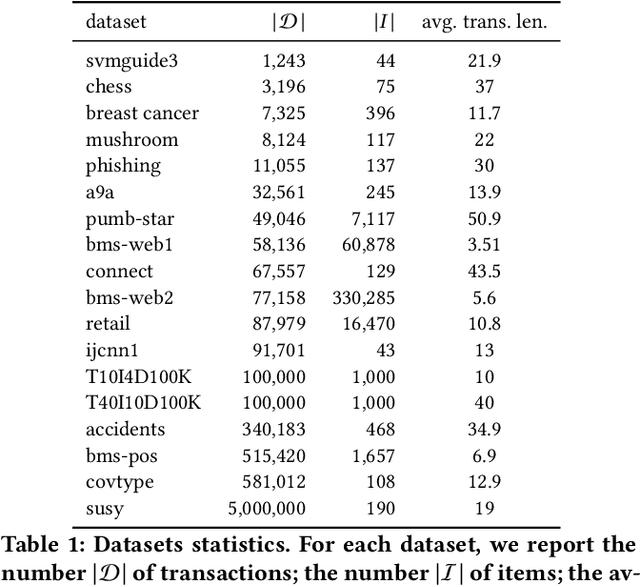
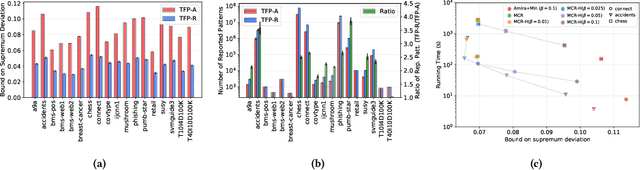
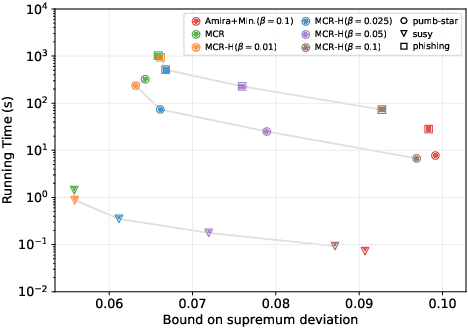
We present MCRapper, an algorithm for efficient computation of Monte-Carlo Empirical Rademacher Averages (MCERA) for families of functions exhibiting poset (e.g., lattice) structure, such as those that arise in many pattern mining tasks. The MCERA allows us to compute upper bounds to the maximum deviation of sample means from their expectations, thus it can be used to find both statistically-significant functions (i.e., patterns) when the available data is seen as a sample from an unknown distribution, and approximations of collections of high-expectation functions (e.g., frequent patterns) when the available data is a small sample from a large dataset. This feature is a strong improvement over previously proposed solutions that could only achieve one of the two. MCRapper uses upper bounds to the discrepancy of the functions to efficiently explore and prune the search space, a technique borrowed from pattern mining itself. To show the practical use of MCRapper, we employ it to develop an algorithm TFP-R for the task of True Frequent Pattern (TFP) mining. TFP-R gives guarantees on the probability of including any false positives (precision) and exhibits higher statistical power (recall) than existing methods offering the same guarantees. We evaluate MCRapper and TFP-R and show that they outperform the state-of-the-art for their respective tasks.

Finding the True Frequent Itemsets

Frequent Itemsets (FIs) mining is a fundamental primitive in data mining. It requires to identify all itemsets appearing in at least a fraction $\theta$ of a transactional dataset $\mathcal{D}$. Often though, the ultimate goal of mining $\mathcal{D}$ is not an analysis of the dataset \emph{per se}, but the understanding of the underlying process that generated it. Specifically, in many applications $\mathcal{D}$ is a collection of samples obtained from an unknown probability distribution $\pi$ on transactions, and by extracting the FIs in $\mathcal{D}$ one attempts to infer itemsets that are frequently (i.e., with probability at least $\theta$) generated by $\pi$, which we call the True Frequent Itemsets (TFIs). Due to the inherently stochastic nature of the generative process, the set of FIs is only a rough approximation of the set of TFIs, as it often contains a huge number of \emph{false positives}, i.e., spurious itemsets that are not among the TFIs. In this work we design and analyze an algorithm to identify a threshold $\hat{\theta}$ such that the collection of itemsets with frequency at least $\hat{\theta}$ in $\mathcal{D}$ contains only TFIs with probability at least $1-\delta$, for some user-specified $\delta$. Our method uses results from statistical learning theory involving the (empirical) VC-dimension of the problem at hand. This allows us to identify almost all the TFIs without including any false positive. We also experimentally compare our method with the direct mining of $\mathcal{D}$ at frequency $\theta$ and with techniques based on widely-used standard bounds (i.e., the Chernoff bounds) of the binomial distribution, and show that our algorithm outperforms these methods and achieves even better results than what is guaranteed by the theoretical analysis.

Efficient Discovery of Association Rules and Frequent Itemsets through Sampling with Tight Performance Guarantees

The tasks of extracting (top-$K$) Frequent Itemsets (FI's) and Association Rules (AR's) are fundamental primitives in data mining and database applications. Exact algorithms for these problems exist and are widely used, but their running time is hindered by the need of scanning the entire dataset, possibly multiple times. High quality approximations of FI's and AR's are sufficient for most practical uses, and a number of recent works explored the application of sampling for fast discovery of approximate solutions to the problems. However, these works do not provide satisfactory performance guarantees on the quality of the approximation, due to the difficulty of bounding the probability of under- or over-sampling any one of an unknown number of frequent itemsets. In this work we circumvent this issue by applying the statistical concept of \emph{Vapnik-Chervonenkis (VC) dimension} to develop a novel technique for providing tight bounds on the sample size that guarantees approximation within user-specified parameters. Our technique applies both to absolute and to relative approximations of (top-$K$) FI's and AR's. The resulting sample size is linearly dependent on the VC-dimension of a range space associated with the dataset to be mined. The main theoretical contribution of this work is a proof that the VC-dimension of this range space is upper bounded by an easy-to-compute characteristic quantity of the dataset which we call \emph{d-index}, and is the maximum integer $d$ such that the dataset contains at least $d$ transactions of length at least $d$ such that no one of them is a superset of or equal to another. We show that this bound is strict for a large class of datasets.

The VC-Dimension of Queries and Selectivity Estimation Through Sampling

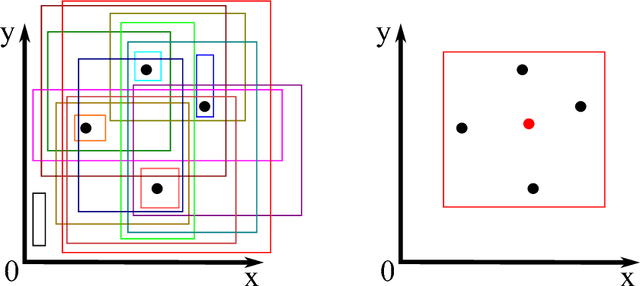
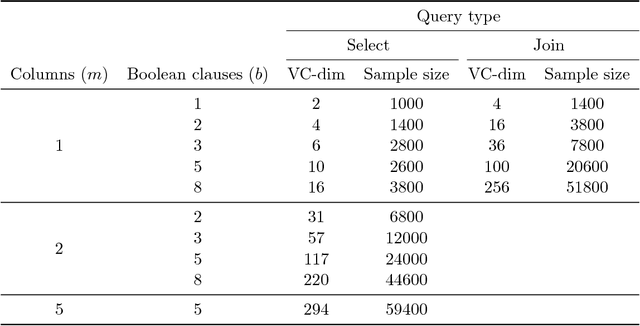
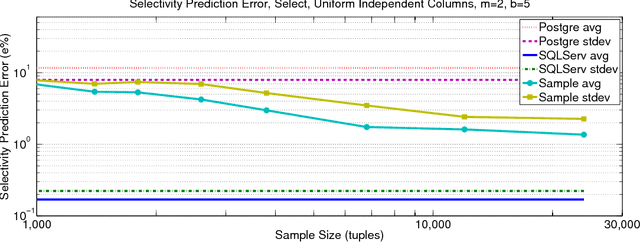
We develop a novel method, based on the statistical concept of the Vapnik-Chervonenkis dimension, to evaluate the selectivity (output cardinality) of SQL queries - a crucial step in optimizing the execution of large scale database and data-mining operations. The major theoretical contribution of this work, which is of independent interest, is an explicit bound to the VC-dimension of a range space defined by all possible outcomes of a collection (class) of queries. We prove that the VC-dimension is a function of the maximum number of Boolean operations in the selection predicate and of the maximum number of select and join operations in any individual query in the collection, but it is neither a function of the number of queries in the collection nor of the size (number of tuples) of the database. We leverage on this result and develop a method that, given a class of queries, builds a concise random sample of a database, such that with high probability the execution of any query in the class on the sample provides an accurate estimate for the selectivity of the query on the original large database. The error probability holds simultaneously for the selectivity estimates of all queries in the collection, thus the same sample can be used to evaluate the selectivity of multiple queries, and the sample needs to be refreshed only following major changes in the database. The sample representation computed by our method is typically sufficiently small to be stored in main memory. We present extensive experimental results, validating our theoretical analysis and demonstrating the advantage of our technique when compared to complex selectivity estimation techniques used in PostgreSQL and the Microsoft SQL Server.