Scalable Rule Lists Learning with Sampling

Learning interpretable models has become a major focus of machine learning research, given the increasing prominence of machine learning in socially important decision-making. Among interpretable models, rule lists are among the best-known and easily interpretable ones. However, finding optimal rule lists is computationally challenging, and current approaches are impractical for large datasets. We present a novel and scalable approach to learn nearly optimal rule lists from large datasets. Our algorithm uses sampling to efficiently obtain an approximation of the optimal rule list with rigorous guarantees on the quality of the approximation. In particular, our algorithm guarantees to find a rule list with accuracy very close to the optimal rule list when a rule list with high accuracy exists. Our algorithm builds on the VC-dimension of rule lists, for which we prove novel upper and lower bounds. Our experimental evaluation on large datasets shows that our algorithm identifies nearly optimal rule lists with a speed-up up to two orders of magnitude over state-of-the-art exact approaches. Moreover, our algorithm is as fast as, and sometimes faster than, recent heuristic approaches, while reporting higher quality rule lists. In addition, the rules reported by our algorithm are more similar to the rules in the optimal rule list than the rules from heuristic approaches.

Efficient Discovery of Significant Patterns with Few-Shot Resampling

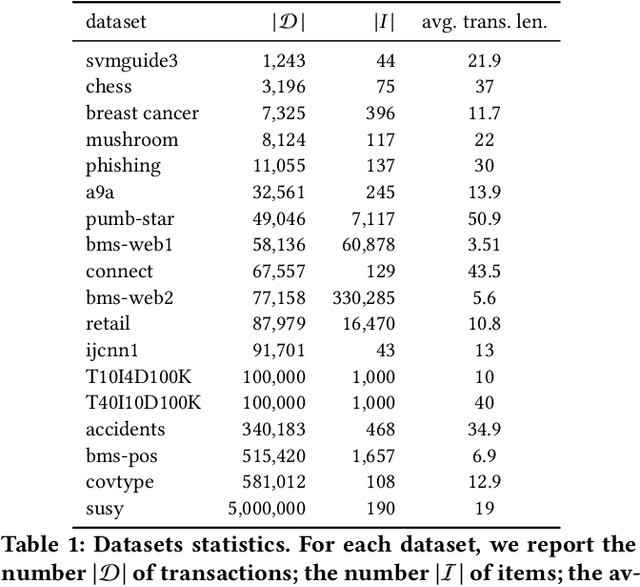
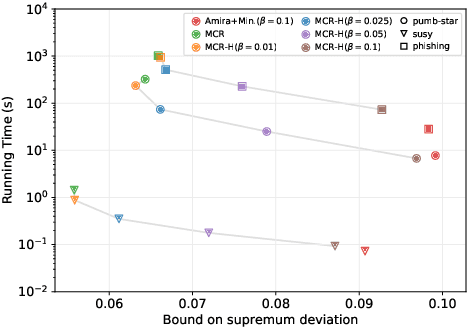
Significant pattern mining is a fundamental task in mining transactional data, requiring to identify patterns significantly associated with the value of a given feature, the target. In several applications, such as biomedicine, basket market analysis, and social networks, the goal is to discover patterns whose association with the target is defined with respect to an underlying population, or process, of which the dataset represents only a collection of observations, or samples. A natural way to capture the association of a pattern with the target is to consider its statistical significance, assessing its deviation from the (null) hypothesis of independence between the pattern and the target. While several algorithms have been proposed to find statistically significant patterns, it remains a computationally demanding task, and for complex patterns such as subgroups, no efficient solution exists. We present FSR, an efficient algorithm to identify statistically significant patterns with rigorous guarantees on the probability of false discoveries. FSR builds on a novel general framework for mining significant patterns that captures some of the most commonly considered patterns, including itemsets, sequential patterns, and subgroups. FSR uses a small number of resampled datasets, obtained by assigning i.i.d. labels to each transaction, to rigorously bound the supremum deviation of a quality statistic measuring the significance of patterns. FSR builds on novel tight bounds on the supremum deviation that require to mine a small number of resampled datasets, while providing a high effectiveness in discovering significant patterns. As a test case, we consider significant subgroup mining, and our evaluation on several real datasets shows that FSR is effective in discovering significant subgroups, while requiring a small number of resampled datasets.

Sharper convergence bounds of Monte Carlo Rademacher Averages through Self-Bounding functions

We derive sharper probabilistic concentration bounds for the Monte Carlo Empirical Rademacher Averages (MCERA), which are proved through recent results on the concentration of self-bounding functions. Our novel bounds allow obtaining sharper bounds to (Local) Rademacher Averages. We also derive novel variance-aware bounds for the special case where only one vector of Rademacher random variables is used to compute the MCERA. Then, we leverage the framework of self-bounding functions to derive novel probabilistic bounds to the supremum deviations, that may be of independent interest.

MCRapper: Monte-Carlo Rademacher Averages for Poset Families and Approximate Pattern Mining

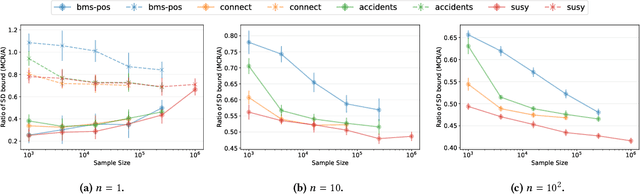
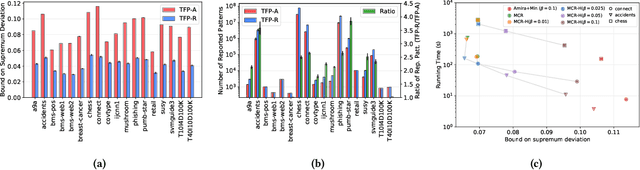
We present MCRapper, an algorithm for efficient computation of Monte-Carlo Empirical Rademacher Averages (MCERA) for families of functions exhibiting poset (e.g., lattice) structure, such as those that arise in many pattern mining tasks. The MCERA allows us to compute upper bounds to the maximum deviation of sample means from their expectations, thus it can be used to find both statistically-significant functions (i.e., patterns) when the available data is seen as a sample from an unknown distribution, and approximations of collections of high-expectation functions (e.g., frequent patterns) when the available data is a small sample from a large dataset. This feature is a strong improvement over previously proposed solutions that could only achieve one of the two. MCRapper uses upper bounds to the discrepancy of the functions to efficiently explore and prune the search space, a technique borrowed from pattern mining itself. To show the practical use of MCRapper, we employ it to develop an algorithm TFP-R for the task of True Frequent Pattern (TFP) mining. TFP-R gives guarantees on the probability of including any false positives (precision) and exhibits higher statistical power (recall) than existing methods offering the same guarantees. We evaluate MCRapper and TFP-R and show that they outperform the state-of-the-art for their respective tasks.