An Axiomatic Theory of Provably-Fair Welfare-Centric Machine Learning
Paper and Code
Apr 29, 2021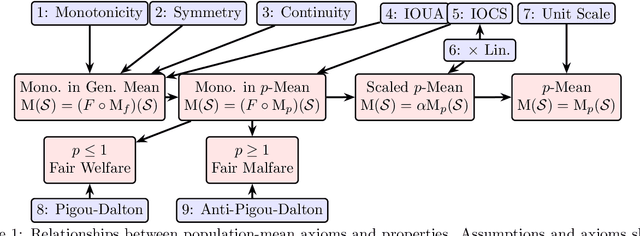
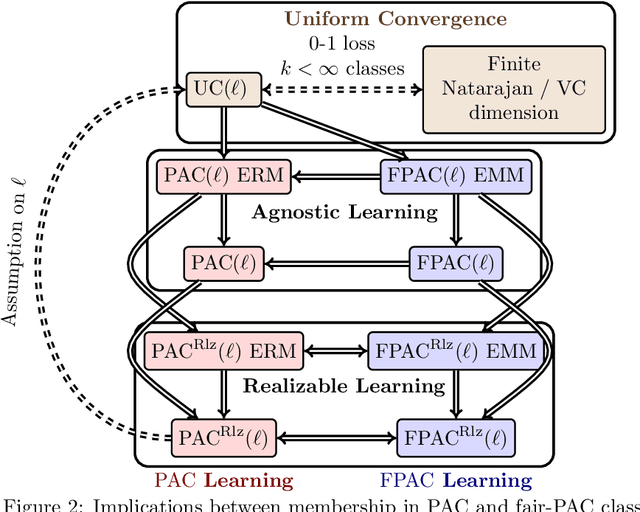
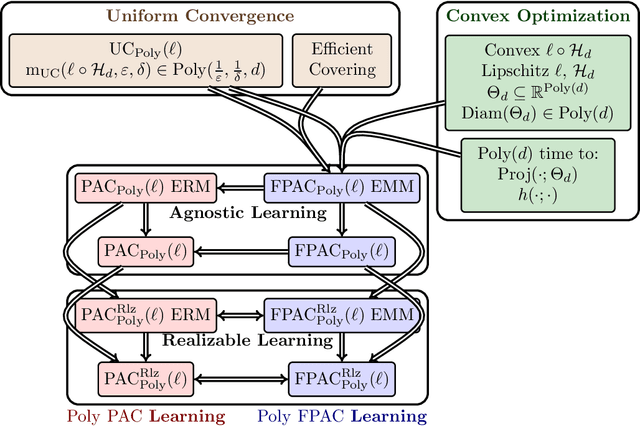
We address an inherent difficulty in welfare-theoretic fair machine learning, proposing an equivalently-axiomatically justified alternative, and studying the resulting computational and statistical learning questions. Welfare metrics quantify overall wellbeing across a population of one or more groups, and welfare-based objectives and constraints have recently been proposed to incentivize fair machine learning methods to produce satisfactory solutions that consider the diverse needs of multiple groups. Unfortunately, many machine-learning problems are more naturally cast as loss minimization, rather than utility maximization tasks, which complicates direct application of welfare-centric methods to fair-ML tasks. In this work, we define a complementary measure, termed malfare, measuring overall societal harm (rather than wellbeing), with axiomatic justification via the standard axioms of cardinal welfare. We then cast fair machine learning as a direct malfare minimization problem, where a group's malfare is their risk (expected loss). Surprisingly, the axioms of cardinal welfare (malfare) dictate that this is not equivalent to simply defining utility as negative loss. Building upon these concepts, we define fair-PAC learning, where a fair PAC-learner is an algorithm that learns an $\varepsilon$-$\delta$ malfare-optimal model with bounded sample complexity, for any data distribution, and for any malfare concept. We show broad conditions under which, with appropriate modifications, many standard PAC-learners may be converted to fair-PAC learners. This places fair-PAC learning on firm theoretical ground, as it yields statistical, and in some cases computational, efficiency guarantees for many well-studied machine-learning models, and is also practically relevant, as it democratizes fair ML by providing concrete training algorithms and rigorous generalization guarantees for these models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge