Percentile Criterion Optimization in Offline Reinforcement Learning

In reinforcement learning, robust policies for high-stakes decision-making problems with limited data are usually computed by optimizing the \emph{percentile criterion}. The percentile criterion is approximately solved by constructing an \emph{ambiguity set} that contains the true model with high probability and optimizing the policy for the worst model in the set. Since the percentile criterion is non-convex, constructing ambiguity sets is often challenging. Existing work uses \emph{Bayesian credible regions} as ambiguity sets, but they are often unnecessarily large and result in learning overly conservative policies. To overcome these shortcomings, we propose a novel Value-at-Risk based dynamic programming algorithm to optimize the percentile criterion without explicitly constructing any ambiguity sets. Our theoretical and empirical results show that our algorithm implicitly constructs much smaller ambiguity sets and learns less conservative robust policies.

Soft-Robust Algorithms for Handling Model Misspecification

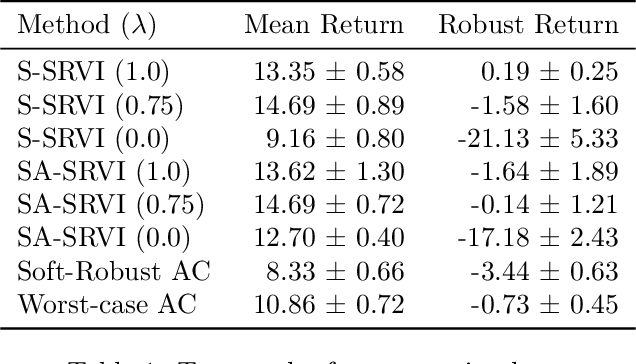
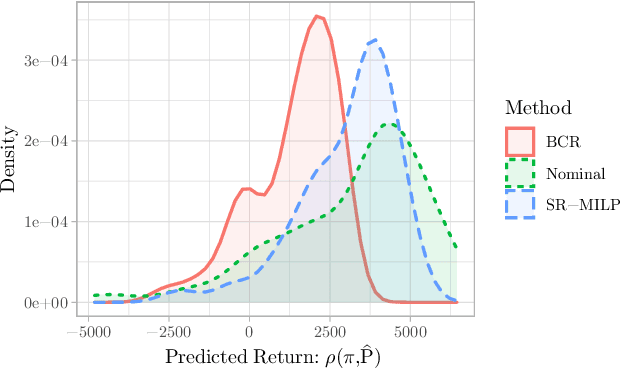
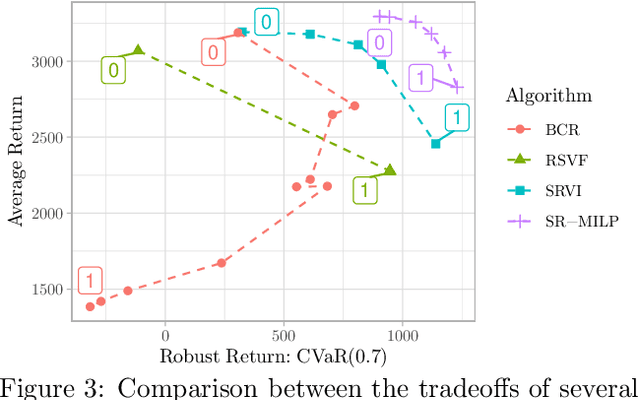
In reinforcement learning, robust policies for high-stakes decision-making problems with limited data are usually computed by optimizing the percentile criterion, which minimizes the probability of a catastrophic failure. Unfortunately, such policies are typically overly conservative as the percentile criterion is non-convex, difficult to optimize, and ignores the mean performance. To overcome these shortcomings, we study the soft-robust criterion, which uses risk measures to balance the mean and percentile criteria better. In this paper, we establish the soft-robust criterion's fundamental properties, show that it is NP-hard to optimize, and propose and analyze two algorithms to optimize it approximately. Our theoretical analyses and empirical evaluations demonstrate that our algorithms compute much less conservative solutions than the existing approximate methods for optimizing the percentile-criterion.