Soft-Robust Algorithms for Handling Model Misspecification
Paper and Code
Nov 30, 2020
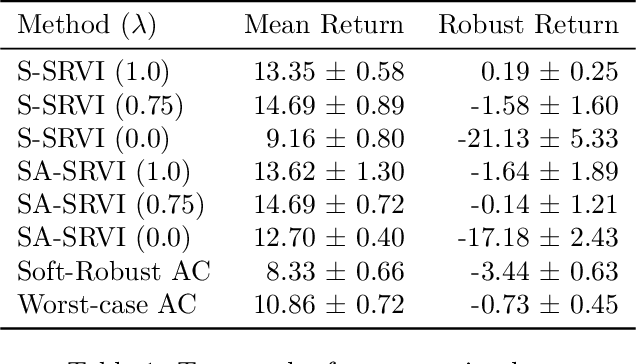
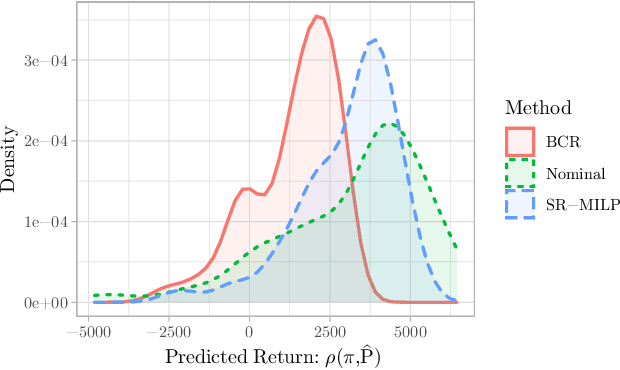
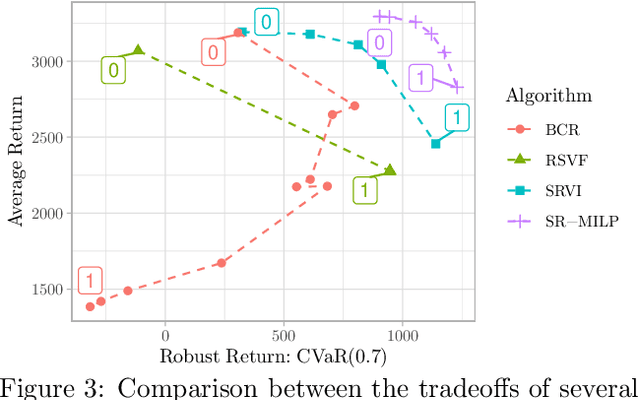
In reinforcement learning, robust policies for high-stakes decision-making problems with limited data are usually computed by optimizing the percentile criterion, which minimizes the probability of a catastrophic failure. Unfortunately, such policies are typically overly conservative as the percentile criterion is non-convex, difficult to optimize, and ignores the mean performance. To overcome these shortcomings, we study the soft-robust criterion, which uses risk measures to balance the mean and percentile criteria better. In this paper, we establish the soft-robust criterion's fundamental properties, show that it is NP-hard to optimize, and propose and analyze two algorithms to optimize it approximately. Our theoretical analyses and empirical evaluations demonstrate that our algorithms compute much less conservative solutions than the existing approximate methods for optimizing the percentile-criterion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge