Effects of Different Prompts on the Quality of GPT-4 Responses to Dementia Care Questions

Evidence suggests that different prompts lead large language models (LLMs) to generate responses with varying quality. Yet, little is known about prompts' effects on response quality in healthcare domains. In this exploratory study, we address this gap, focusing on a specific healthcare domain: dementia caregiving. We first developed an innovative prompt template with three components: (1) system prompts (SPs) featuring 4 different roles; (2) an initialization prompt; and (3) task prompts (TPs) specifying different levels of details, totaling 12 prompt combinations. Next, we selected 3 social media posts containing complicated, real-world questions about dementia caregivers' challenges in 3 areas: memory loss and confusion, aggression, and driving. We then entered these posts into GPT-4, with our 12 prompts, to generate 12 responses per post, totaling 36 responses. We compared the word count of the 36 responses to explore potential differences in response length. Two experienced dementia care clinicians on our team assessed the response quality using a rating scale with 5 quality indicators: factual, interpretation, application, synthesis, and comprehensiveness (scoring range: 0-5; higher scores indicate higher quality).

Correlated Logistic Model With Elastic Net Regularization for Multilabel Image Classification

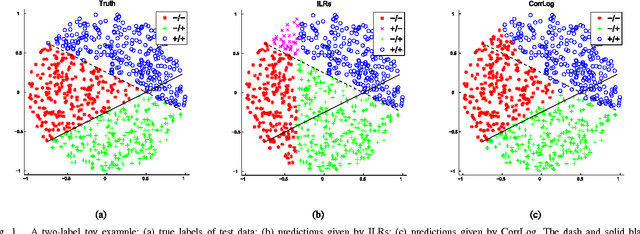
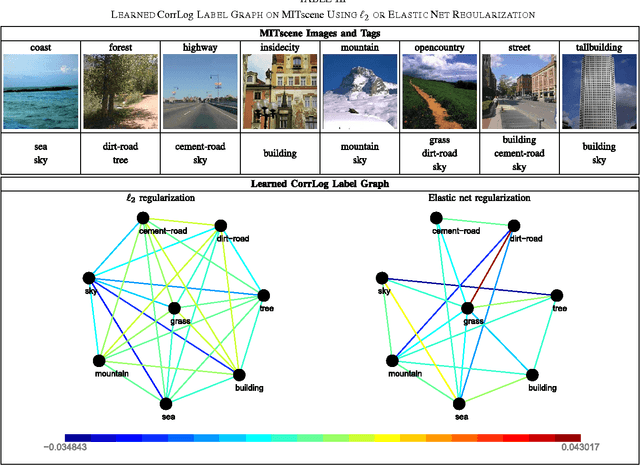
In this paper, we present correlated logistic (CorrLog) model for multilabel image classification. CorrLog extends conventional logistic regression model into multilabel cases, via explicitly modeling the pairwise correlation between labels. In addition, we propose to learn the model parameters of CorrLog with elastic net regularization, which helps exploit the sparsity in feature selection and label correlations and thus further boost the performance of multilabel classification. CorrLog can be efficiently learned, though approximately, by regularized maximum pseudo likelihood estimation, and it enjoys a satisfying generalization bound that is independent of the number of labels. CorrLog performs competitively for multilabel image classification on benchmark data sets MULAN scene, MIT outdoor scene, PASCAL VOC 2007, and PASCAL VOC 2012, compared with the state-of-the-art multilabel classification algorithms.

Deep Semi-Random Features for Nonlinear Function Approximation

We propose semi-random features for nonlinear function approximation. The flexibility of semi-random feature lies between the fully adjustable units in deep learning and the random features used in kernel methods. For one hidden layer models with semi-random features, we prove with no unrealistic assumptions that the model classes contain an arbitrarily good function as the width increases (universality), and despite non-convexity, we can find such a good function (optimization theory) that generalizes to unseen new data (generalization bound). For deep models, with no unrealistic assumptions, we prove universal approximation ability, a lower bound on approximation error, a partial optimization guarantee, and a generalization bound. Depending on the problems, the generalization bound of deep semi-random features can be exponentially better than the known bounds of deep ReLU nets; our generalization error bound can be independent of the depth, the number of trainable weights as well as the input dimensionality. In experiments, we show that semi-random features can match the performance of neural networks by using slightly more units, and it outperforms random features by using significantly fewer units. Moreover, we introduce a new implicit ensemble method by using semi-random features.

On the Complexity of Learning Neural Networks

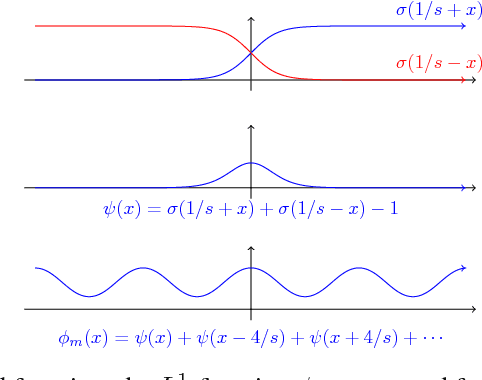
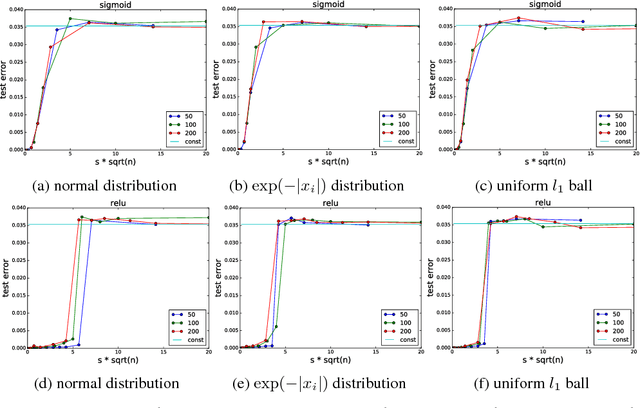
The stunning empirical successes of neural networks currently lack rigorous theoretical explanation. What form would such an explanation take, in the face of existing complexity-theoretic lower bounds? A first step might be to show that data generated by neural networks with a single hidden layer, smooth activation functions and benign input distributions can be learned efficiently. We demonstrate here a comprehensive lower bound ruling out this possibility: for a wide class of activation functions (including all currently used), and inputs drawn from any logconcave distribution, there is a family of one-hidden-layer functions whose output is a sum gate, that are hard to learn in a precise sense: any statistical query algorithm (which includes all known variants of stochastic gradient descent with any loss function) needs an exponential number of queries even using tolerance inversely proportional to the input dimensionality. Moreover, this hard family of functions is realizable with a small (sublinear in dimension) number of activation units in the single hidden layer. The lower bound is also robust to small perturbations of the true weights. Systematic experiments illustrate a phase transition in the training error as predicted by the analysis.

Diverse Neural Network Learns True Target Functions

Neural networks are a powerful class of functions that can be trained with simple gradient descent to achieve state-of-the-art performance on a variety of applications. Despite their practical success, there is a paucity of results that provide theoretical guarantees on why they are so effective. Lying in the center of the problem is the difficulty of analyzing the non-convex loss function with potentially numerous local minima and saddle points. Can neural networks corresponding to the stationary points of the loss function learn the true target function? If yes, what are the key factors contributing to such nice optimization properties? In this paper, we answer these questions by analyzing one-hidden-layer neural networks with ReLU activation, and show that despite the non-convexity, neural networks with diverse units have no spurious local minima. We bypass the non-convexity issue by directly analyzing the first order optimality condition, and show that the loss can be made arbitrarily small if the minimum singular value of the "extended feature matrix" is large enough. We make novel use of techniques from kernel methods and geometric discrepancy, and identify a new relation linking the smallest singular value to the spectrum of a kernel function associated with the activation function and to the diversity of the units. Our results also suggest a novel regularization function to promote unit diversity for potentially better generalization.

Communication Efficient Distributed Kernel Principal Component Analysis

Kernel Principal Component Analysis (KPCA) is a key machine learning algorithm for extracting nonlinear features from data. In the presence of a large volume of high dimensional data collected in a distributed fashion, it becomes very costly to communicate all of this data to a single data center and then perform kernel PCA. Can we perform kernel PCA on the entire dataset in a distributed and communication efficient fashion while maintaining provable and strong guarantees in solution quality? In this paper, we give an affirmative answer to the question by developing a communication efficient algorithm to perform kernel PCA in the distributed setting. The algorithm is a clever combination of subspace embedding and adaptive sampling techniques, and we show that the algorithm can take as input an arbitrary configuration of distributed datasets, and compute a set of global kernel principal components with relative error guarantees independent of the dimension of the feature space or the total number of data points. In particular, computing $k$ principal components with relative error $\epsilon$ over $s$ workers has communication cost $\tilde{O}(s \rho k/\epsilon+s k^2/\epsilon^3)$ words, where $\rho$ is the average number of nonzero entries in each data point. Furthermore, we experimented the algorithm with large-scale real world datasets and showed that the algorithm produces a high quality kernel PCA solution while using significantly less communication than alternative approaches.

Scale Up Nonlinear Component Analysis with Doubly Stochastic Gradients

Nonlinear component analysis such as kernel Principle Component Analysis (KPCA) and kernel Canonical Correlation Analysis (KCCA) are widely used in machine learning, statistics and data analysis, but they can not scale up to big datasets. Recent attempts have employed random feature approximations to convert the problem to the primal form for linear computational complexity. However, to obtain high quality solutions, the number of random features should be the same order of magnitude as the number of data points, making such approach not directly applicable to the regime with millions of data points. We propose a simple, computationally efficient, and memory friendly algorithm based on the "doubly stochastic gradients" to scale up a range of kernel nonlinear component analysis, such as kernel PCA, CCA and SVD. Despite the \emph{non-convex} nature of these problems, our method enjoys theoretical guarantees that it converges at the rate $\tilde{O}(1/t)$ to the global optimum, even for the top $k$ eigen subspace. Unlike many alternatives, our algorithm does not require explicit orthogonalization, which is infeasible on big datasets. We demonstrate the effectiveness and scalability of our algorithm on large scale synthetic and real world datasets.

Scalable Kernel Methods via Doubly Stochastic Gradients

The general perception is that kernel methods are not scalable, and neural nets are the methods of choice for nonlinear learning problems. Or have we simply not tried hard enough for kernel methods? Here we propose an approach that scales up kernel methods using a novel concept called "doubly stochastic functional gradients". Our approach relies on the fact that many kernel methods can be expressed as convex optimization problems, and we solve the problems by making two unbiased stochastic approximations to the functional gradient, one using random training points and another using random functions associated with the kernel, and then descending using this noisy functional gradient. We show that a function produced by this procedure after $t$ iterations converges to the optimal function in the reproducing kernel Hilbert space in rate $O(1/t)$, and achieves a generalization performance of $O(1/\sqrt{t})$. This doubly stochasticity also allows us to avoid keeping the support vectors and to implement the algorithm in a small memory footprint, which is linear in number of iterations and independent of data dimension. Our approach can readily scale kernel methods up to the regimes which are dominated by neural nets. We show that our method can achieve competitive performance to neural nets in datasets such as 8 million handwritten digits from MNIST, 2.3 million energy materials from MolecularSpace, and 1 million photos from ImageNet.

Nonparametric Estimation of Multi-View Latent Variable Models

Spectral methods have greatly advanced the estimation of latent variable models, generating a sequence of novel and efficient algorithms with strong theoretical guarantees. However, current spectral algorithms are largely restricted to mixtures of discrete or Gaussian distributions. In this paper, we propose a kernel method for learning multi-view latent variable models, allowing each mixture component to be nonparametric. The key idea of the method is to embed the joint distribution of a multi-view latent variable into a reproducing kernel Hilbert space, and then the latent parameters are recovered using a robust tensor power method. We establish that the sample complexity for the proposed method is quadratic in the number of latent components and is a low order polynomial in the other relevant parameters. Thus, our non-parametric tensor approach to learning latent variable models enjoys good sample and computational efficiencies. Moreover, the non-parametric tensor power method compares favorably to EM algorithm and other existing spectral algorithms in our experiments.