Polynomial Convergence of Gradient Descent for Training One-Hidden-Layer Neural Networks

We analyze Gradient Descent applied to learning a bounded target function on $n$ real-valued inputs by training a neural network with a single hidden layer of nonlinear gates. Our main finding is that GD starting from a randomly initialized network converges in mean squared loss to the minimum error (in 2-norm) of the best approximation of the target function using a polynomial of degree at most $k$. Moreover, the size of the network and number of iterations needed are both bounded by $n^{O(k)}$. The core of our analysis is the following existence theorem, which is of independent interest: for any $\epsilon > 0$, any bounded function that has a degree-$k$ polynomial approximation with error $\epsilon_0$ (in 2-norm), can be approximated to within error $\epsilon_0 + \epsilon$ as a linear combination of $n^{O(k)} \mbox{poly}(1/\epsilon)$ randomly chosen gates from any class of gates whose corresponding activation function has nonzero coefficients in its harmonic expansion for degrees up to $k$. In particular, this applies to training networks of unbiased sigmoids and ReLUs.

On the Complexity of Learning Neural Networks

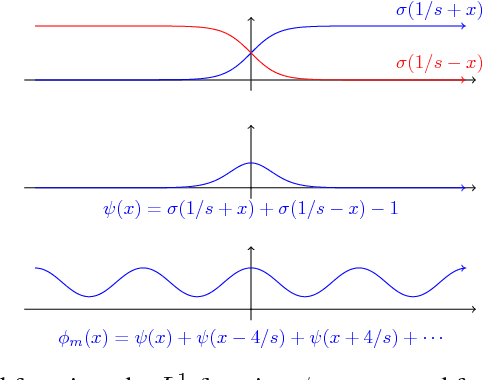
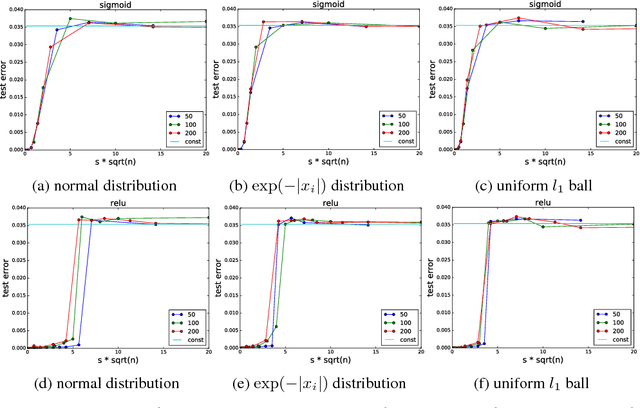
The stunning empirical successes of neural networks currently lack rigorous theoretical explanation. What form would such an explanation take, in the face of existing complexity-theoretic lower bounds? A first step might be to show that data generated by neural networks with a single hidden layer, smooth activation functions and benign input distributions can be learned efficiently. We demonstrate here a comprehensive lower bound ruling out this possibility: for a wide class of activation functions (including all currently used), and inputs drawn from any logconcave distribution, there is a family of one-hidden-layer functions whose output is a sum gate, that are hard to learn in a precise sense: any statistical query algorithm (which includes all known variants of stochastic gradient descent with any loss function) needs an exponential number of queries even using tolerance inversely proportional to the input dimensionality. Moreover, this hard family of functions is realizable with a small (sublinear in dimension) number of activation units in the single hidden layer. The lower bound is also robust to small perturbations of the true weights. Systematic experiments illustrate a phase transition in the training error as predicted by the analysis.