Global-guided Focal Neural Radiance Field for Large-scale Scene Rendering

Neural radiance fields~(NeRF) have recently been applied to render large-scale scenes. However, their limited model capacity typically results in blurred rendering results. Existing large-scale NeRFs primarily address this limitation by partitioning the scene into blocks, which are subsequently handled by separate sub-NeRFs. These sub-NeRFs, trained from scratch and processed independently, lead to inconsistencies in geometry and appearance across the scene. Consequently, the rendering quality fails to exhibit significant improvement despite the expansion of model capacity. In this work, we present global-guided focal neural radiance field (GF-NeRF) that achieves high-fidelity rendering of large-scale scenes. Our proposed GF-NeRF utilizes a two-stage (Global and Focal) architecture and a global-guided training strategy. The global stage obtains a continuous representation of the entire scene while the focal stage decomposes the scene into multiple blocks and further processes them with distinct sub-encoders. Leveraging this two-stage architecture, sub-encoders only need fine-tuning based on the global encoder, thus reducing training complexity in the focal stage while maintaining scene-wide consistency. Spatial information and error information from the global stage also benefit the sub-encoders to focus on crucial areas and effectively capture more details of large-scale scenes. Notably, our approach does not rely on any prior knowledge about the target scene, attributing GF-NeRF adaptable to various large-scale scene types, including street-view and aerial-view scenes. We demonstrate that our method achieves high-fidelity, natural rendering results on various types of large-scale datasets. Our project page: https://shaomq2187.github.io/GF-NeRF/

Unsupervised Domain Adaptation with Implicit Pseudo Supervision for Semantic Segmentation

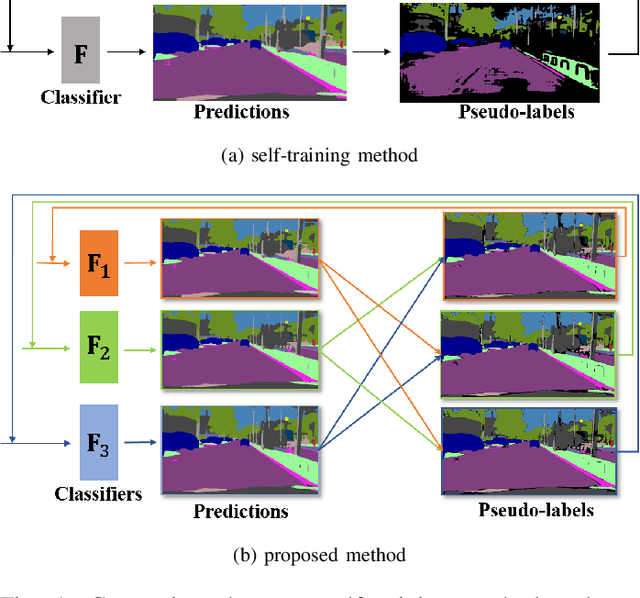
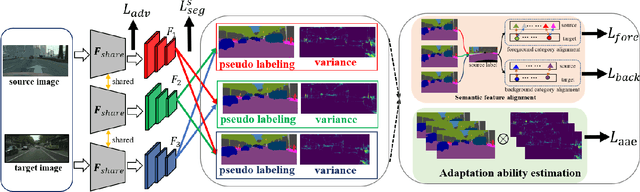
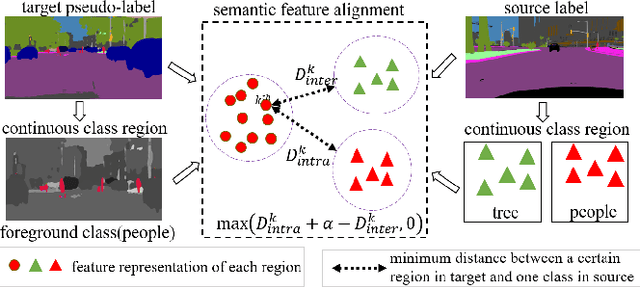
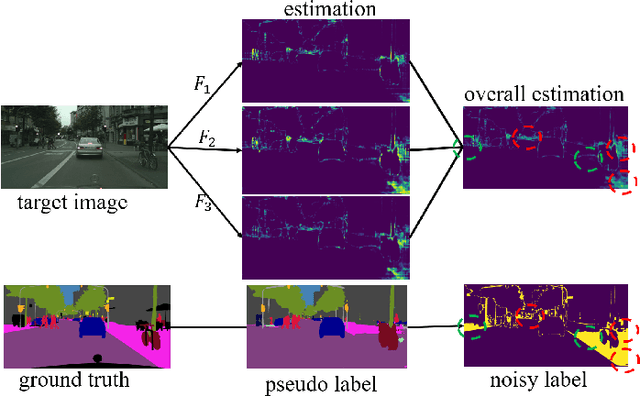
Pseudo-labelling is a popular technique in unsuper-vised domain adaptation for semantic segmentation. However, pseudo labels are noisy and inevitably have confirmation bias due to the discrepancy between source and target domains and training process. In this paper, we train the model by the pseudo labels which are implicitly produced by itself to learn new complementary knowledge about target domain. Specifically, we propose a tri-learning architecture, where every two branches produce the pseudo labels to train the third one. And we align the pseudo labels based on the similarity of the probability distributions for each two branches. To further implicitly utilize the pseudo labels, we maximize the distances of features for different classes and minimize the distances for the same classes by triplet loss. Extensive experiments on GTA5 to Cityscapes and SYNTHIA to Cityscapes tasks show that the proposed method has considerable improvements.

Projected Neural Network for a Class of Sparse Regression with Cardinality Penalty

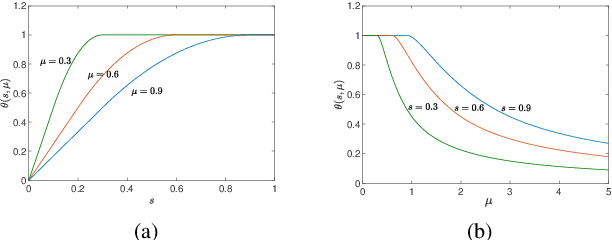
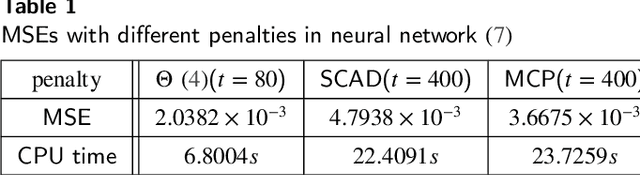
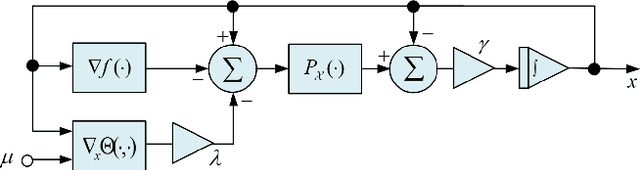
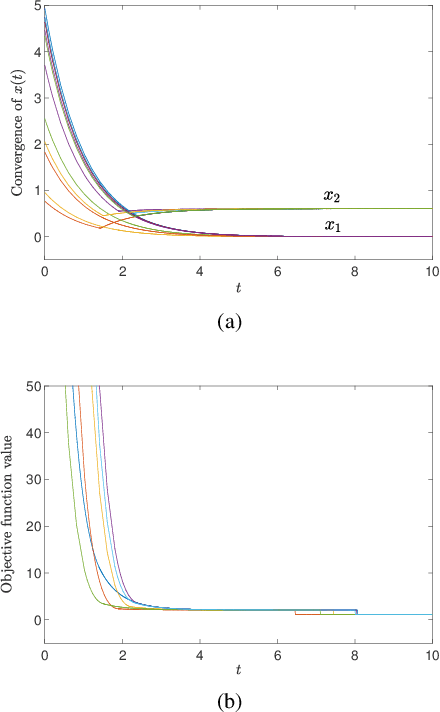
In this paper, we consider a class of sparse regression problems, whose objective function is the summation of a convex loss function and a cardinality penalty. By constructing a smoothing function for the cardinality function, we propose a projected neural network and design a correction method for solving this problem. The solution of the proposed neural network is unique, global existent, bounded and globally Lipschitz continuous. Besides, we prove that all accumulation points of the proposed neural network have a common support set and a unified lower bound for the nonzero entries. Combining the proposed neural network with the correction method, any corrected accumulation point is a local minimizer of the considered sparse regression problem. Moreover, we analyze the equivalent relationship on the local minimizers between the considered sparse regression problem and another sparse problem. Finally, some numerical experiments are provided to show the efficiency of the proposed neural networks in solving some sparse regression problems in practice.

Repulsive Mixture Models of Exponential Family PCA for Clustering

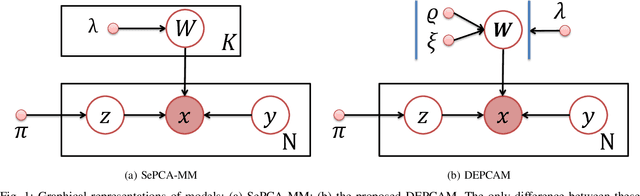
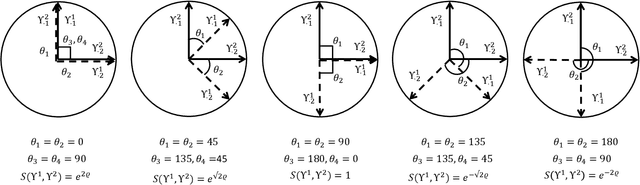
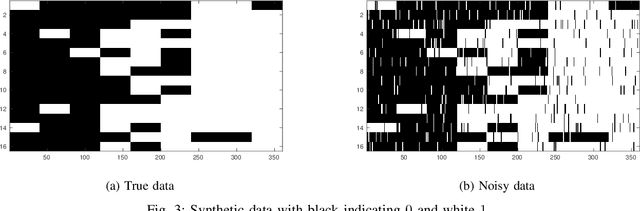
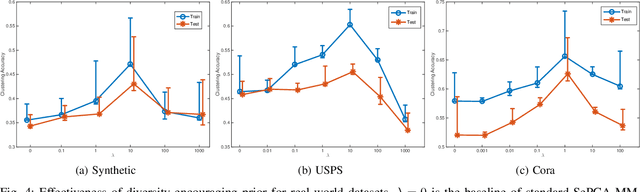
The mixture extension of exponential family principal component analysis (EPCA) was designed to encode much more structural information about data distribution than the traditional EPCA does. For example, due to the linearity of EPCA's essential form, nonlinear cluster structures cannot be easily handled, but they are explicitly modeled by the mixing extensions. However, the traditional mixture of local EPCAs has the problem of model redundancy, i.e., overlaps among mixing components, which may cause ambiguity for data clustering. To alleviate this problem, in this paper, a repulsiveness-encouraging prior is introduced among mixing components and a diversified EPCA mixture (DEPCAM) model is developed in the Bayesian framework. Specifically, a determinantal point process (DPP) is exploited as a diversity-encouraging prior distribution over the joint local EPCAs. As required, a matrix-valued measure for L-ensemble kernel is designed, within which, $\ell_1$ constraints are imposed to facilitate selecting effective PCs of local EPCAs, and angular based similarity measure are proposed. An efficient variational EM algorithm is derived to perform parameter learning and hidden variable inference. Experimental results on both synthetic and real-world datasets confirm the effectiveness of the proposed method in terms of model parsimony and generalization ability on unseen test data.

Detecting Communities in Heterogeneous Multi-Relational Networks:A Message Passing based Approach

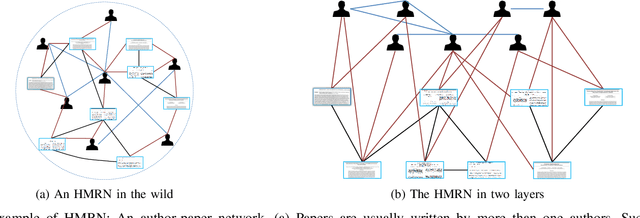
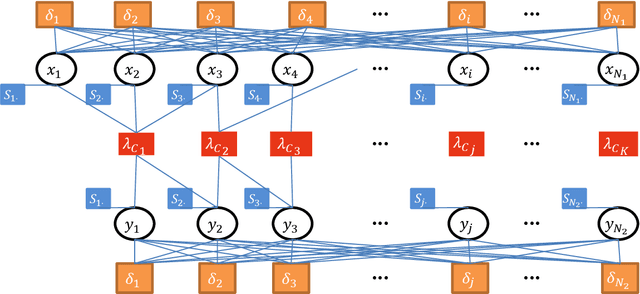
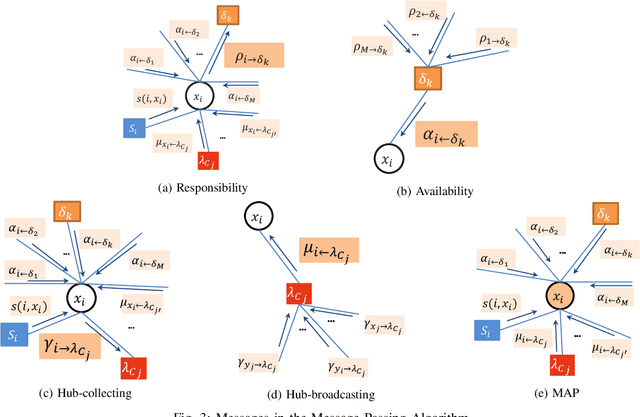
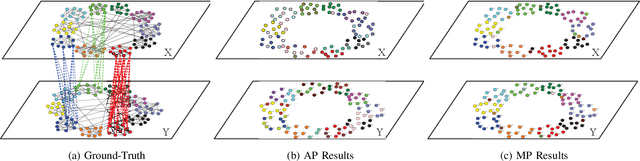
Community is a common characteristic of networks including social networks, biological networks, computer and information networks, to name a few. Community detection is a basic step for exploring and analysing these network data. Typically, homogenous network is a type of networks which consists of only one type of objects with one type of links connecting them. There has been a large body of developments in models and algorithms to detect communities over it. However, real-world networks naturally exhibit heterogeneous qualities appearing as multiple types of objects with multi-relational links connecting them. Those heterogeneous information could facilitate the community detection for its constituent homogeneous networks, but has not been fully explored. In this paper, we exploit heterogeneous multi-relational networks (HMRNet) and propose an efficient message passing based algorithm to simultaneously detect communities for all homogeneous networks. Specifically, an HMRNet is reorganized into a hierarchical structure with homogeneous networks as its layers and heterogeneous links connecting them. To detect communities in such an HMRNet, the problem is formulated as a maximum a posterior (MAP) over a factor graph. Finally a message passing based algorithm is derived to find a best solution of the MAP problem. Evaluation on both synthetic and real-world networks confirms the effectiveness of the proposed method.

Correlated Logistic Model With Elastic Net Regularization for Multilabel Image Classification

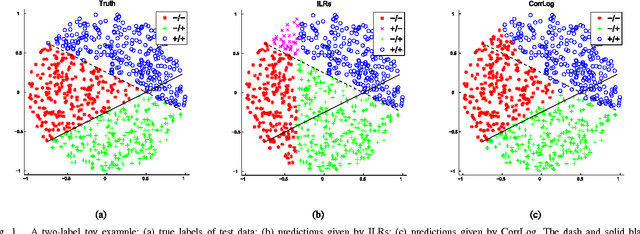
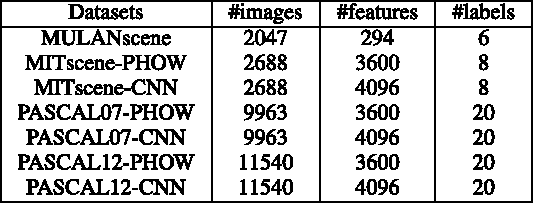
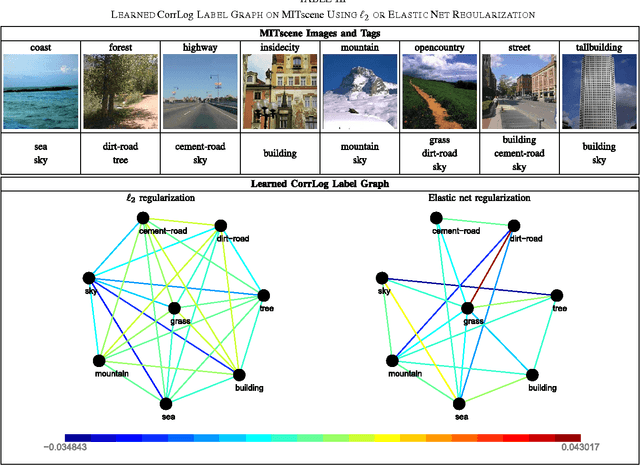
In this paper, we present correlated logistic (CorrLog) model for multilabel image classification. CorrLog extends conventional logistic regression model into multilabel cases, via explicitly modeling the pairwise correlation between labels. In addition, we propose to learn the model parameters of CorrLog with elastic net regularization, which helps exploit the sparsity in feature selection and label correlations and thus further boost the performance of multilabel classification. CorrLog can be efficiently learned, though approximately, by regularized maximum pseudo likelihood estimation, and it enjoys a satisfying generalization bound that is independent of the number of labels. CorrLog performs competitively for multilabel image classification on benchmark data sets MULAN scene, MIT outdoor scene, PASCAL VOC 2007, and PASCAL VOC 2012, compared with the state-of-the-art multilabel classification algorithms.

Diversified Hidden Markov Models for Sequential Labeling

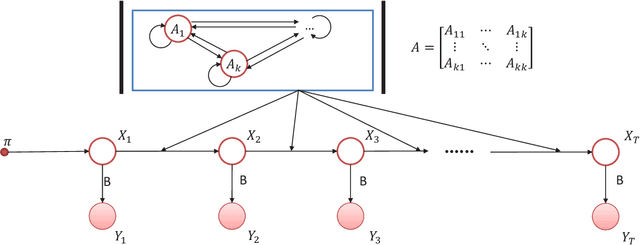
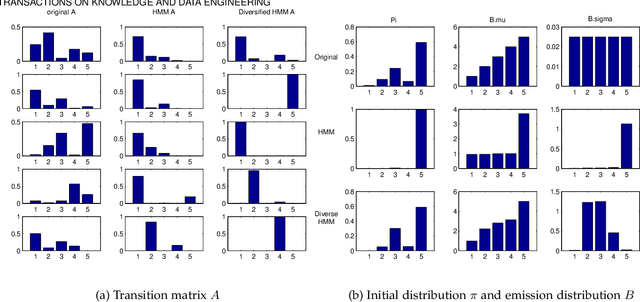
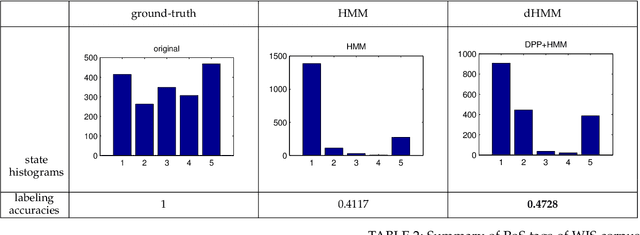
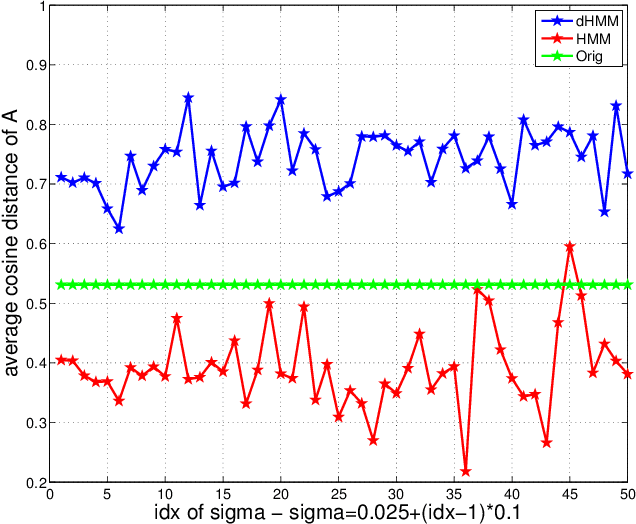
Labeling of sequential data is a prevalent meta-problem for a wide range of real world applications. While the first-order Hidden Markov Models (HMM) provides a fundamental approach for unsupervised sequential labeling, the basic model does not show satisfying performance when it is directly applied to real world problems, such as part-of-speech tagging (PoS tagging) and optical character recognition (OCR). Aiming at improving performance, important extensions of HMM have been proposed in the literatures. One of the common key features in these extensions is the incorporation of proper prior information. In this paper, we propose a new extension of HMM, termed diversified Hidden Markov Models (dHMM), which utilizes a diversity-encouraging prior over the state-transition probabilities and thus facilitates more dynamic sequential labellings. Specifically, the diversity is modeled by a continuous determinantal point process prior, which we apply to both unsupervised and supervised scenarios. Learning and inference algorithms for dHMM are derived. Empirical evaluations on benchmark datasets for unsupervised PoS tagging and supervised OCR confirmed the effectiveness of dHMM, with competitive performance to the state-of-the-art.

Adapting Stochastic Block Models to Power-Law Degree Distributions

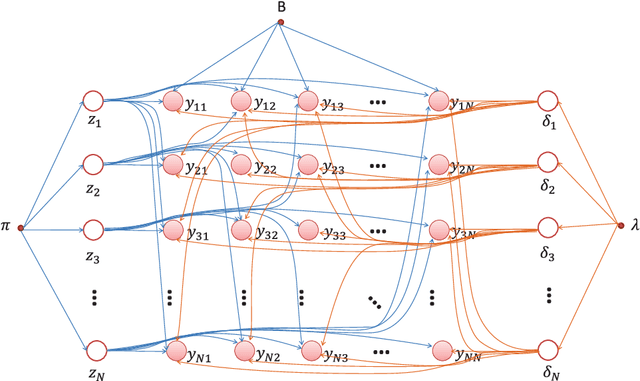
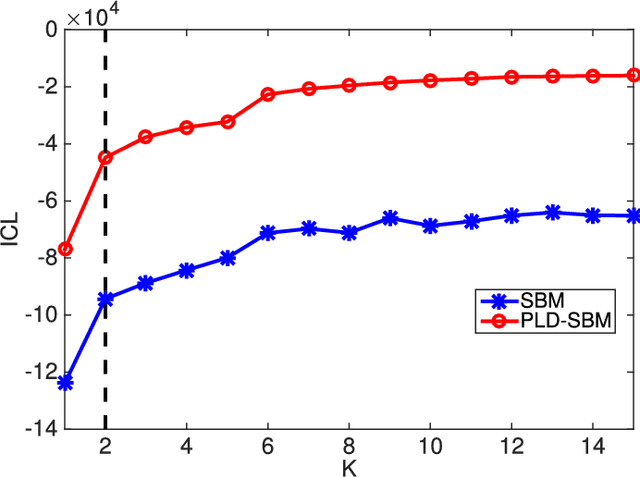
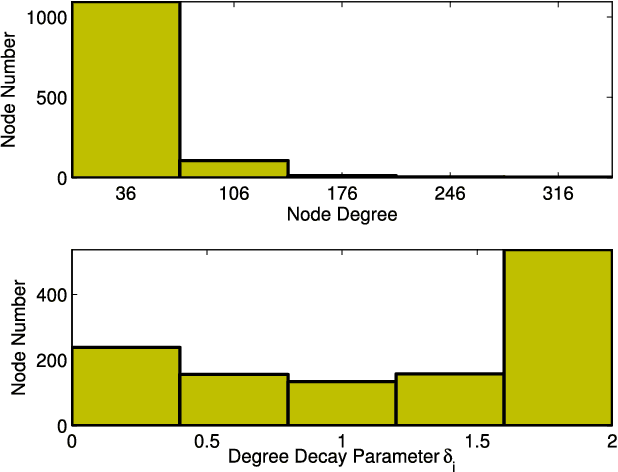
Stochastic block models (SBMs) have been playing an important role in modeling clusters or community structures of network data. But, it is incapable of handling several complex features ubiquitously exhibited in real-world networks, one of which is the power-law degree characteristic. To this end, we propose a new variant of SBM, termed power-law degree SBM (PLD-SBM), by introducing degree decay variables to explicitly encode the varying degree distribution over all nodes. With an exponential prior, it is proved that PLD-SBM approximately preserves the scale-free feature in real networks. In addition, from the inference of variational E-Step, PLD-SBM is indeed to correct the bias inherited in SBM with the introduced degree decay factors. Furthermore, experiments conducted on both synthetic networks and two real-world datasets including Adolescent Health Data and the political blogs network verify the effectiveness of the proposed model in terms of cluster prediction accuracies.

Asymptotic Generalization Bound of Fisher's Linear Discriminant Analysis

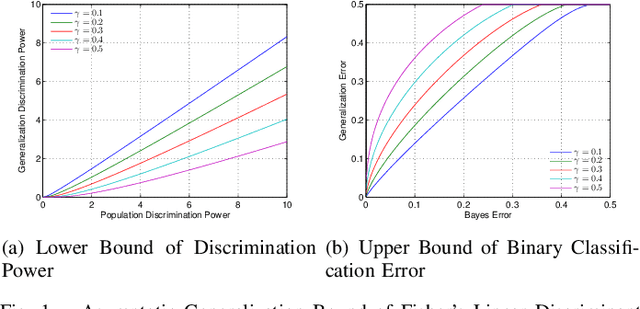
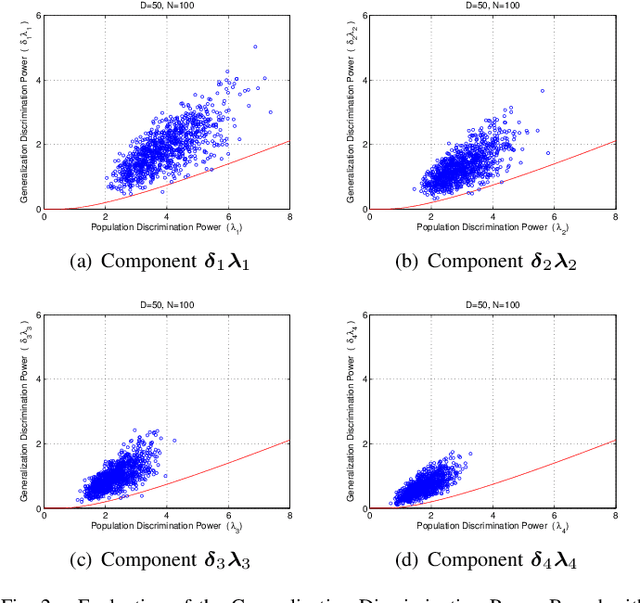
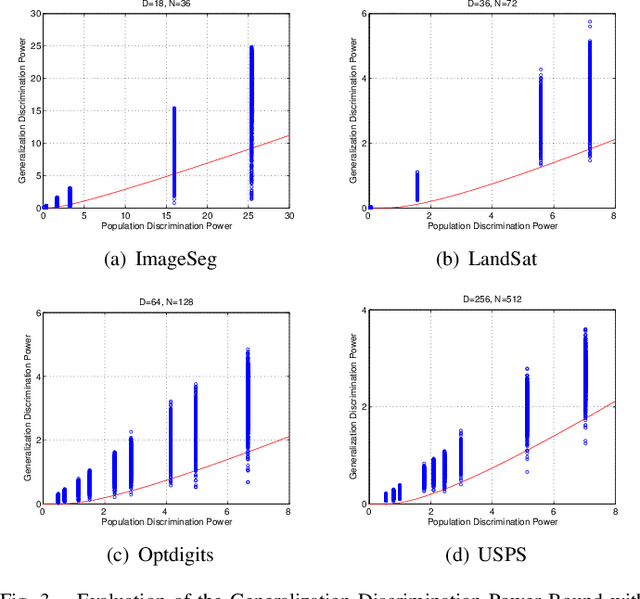
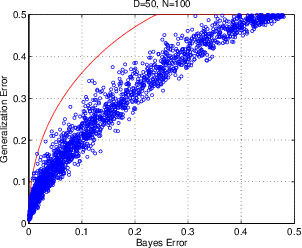
Fisher's linear discriminant analysis (FLDA) is an important dimension reduction method in statistical pattern recognition. It has been shown that FLDA is asymptotically Bayes optimal under the homoscedastic Gaussian assumption. However, this classical result has the following two major limitations: 1) it holds only for a fixed dimensionality $D$, and thus does not apply when $D$ and the training sample size $N$ are proportionally large; 2) it does not provide a quantitative description on how the generalization ability of FLDA is affected by $D$ and $N$. In this paper, we present an asymptotic generalization analysis of FLDA based on random matrix theory, in a setting where both $D$ and $N$ increase and $D/N\longrightarrow\gamma\in[0,1)$. The obtained lower bound of the generalization discrimination power overcomes both limitations of the classical result, i.e., it is applicable when $D$ and $N$ are proportionally large and provides a quantitative description of the generalization ability of FLDA in terms of the ratio $\gamma=D/N$ and the population discrimination power. Besides, the discrimination power bound also leads to an upper bound on the generalization error of binary-classification with FLDA.