Repulsive Mixture Models of Exponential Family PCA for Clustering
Paper and Code
Apr 07, 2020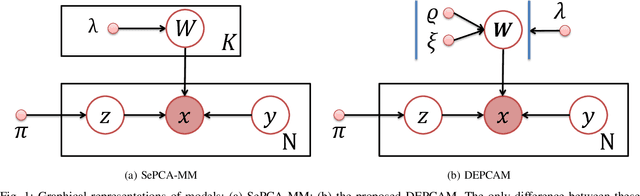
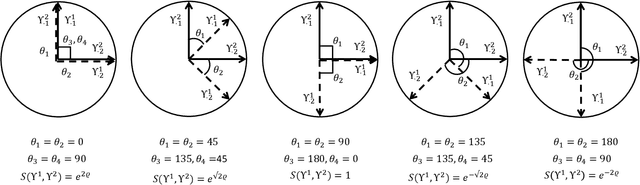
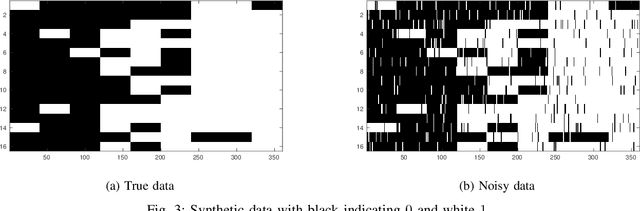
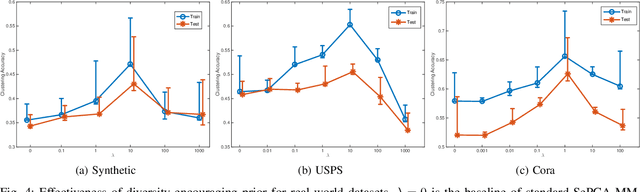
The mixture extension of exponential family principal component analysis (EPCA) was designed to encode much more structural information about data distribution than the traditional EPCA does. For example, due to the linearity of EPCA's essential form, nonlinear cluster structures cannot be easily handled, but they are explicitly modeled by the mixing extensions. However, the traditional mixture of local EPCAs has the problem of model redundancy, i.e., overlaps among mixing components, which may cause ambiguity for data clustering. To alleviate this problem, in this paper, a repulsiveness-encouraging prior is introduced among mixing components and a diversified EPCA mixture (DEPCAM) model is developed in the Bayesian framework. Specifically, a determinantal point process (DPP) is exploited as a diversity-encouraging prior distribution over the joint local EPCAs. As required, a matrix-valued measure for L-ensemble kernel is designed, within which, $\ell_1$ constraints are imposed to facilitate selecting effective PCs of local EPCAs, and angular based similarity measure are proposed. An efficient variational EM algorithm is derived to perform parameter learning and hidden variable inference. Experimental results on both synthetic and real-world datasets confirm the effectiveness of the proposed method in terms of model parsimony and generalization ability on unseen test data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge