Graph Convolutional Neural Networks with Diverse Negative Samples via Decomposed Determinant Point Processes

Graph convolutional networks (GCNs) have achieved great success in graph representation learning by extracting high-level features from nodes and their topology. Since GCNs generally follow a message-passing mechanism, each node aggregates information from its first-order neighbour to update its representation. As a result, the representations of nodes with edges between them should be positively correlated and thus can be considered positive samples. However, there are more non-neighbour nodes in the whole graph, which provide diverse and useful information for the representation update. Two non-adjacent nodes usually have different representations, which can be seen as negative samples. Besides the node representations, the structural information of the graph is also crucial for learning. In this paper, we used quality-diversity decomposition in determinant point processes (DPP) to obtain diverse negative samples. When defining a distribution on diverse subsets of all non-neighbouring nodes, we incorporate both graph structure information and node representations. Since the DPP sampling process requires matrix eigenvalue decomposition, we propose a new shortest-path-base method to improve computational efficiency. Finally, we incorporate the obtained negative samples into the graph convolution operation. The ideas are evaluated empirically in experiments on node classification tasks. These experiments show that the newly proposed methods not only improve the overall performance of standard representation learning but also significantly alleviate over-smoothing problems.

Learning from the Dark: Boosting Graph Convolutional Neural Networks with Diverse Negative Samples

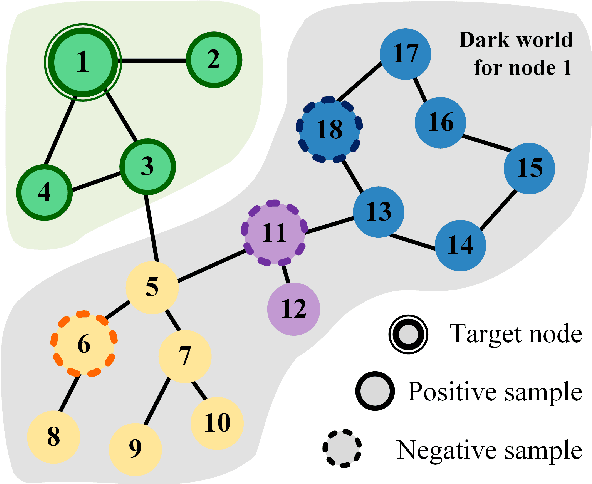
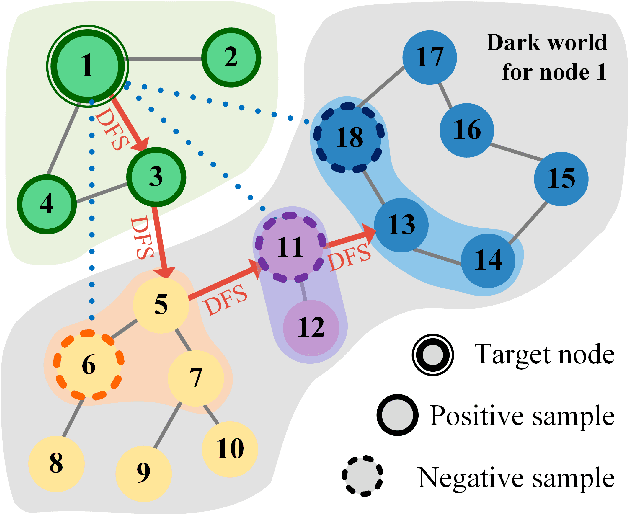
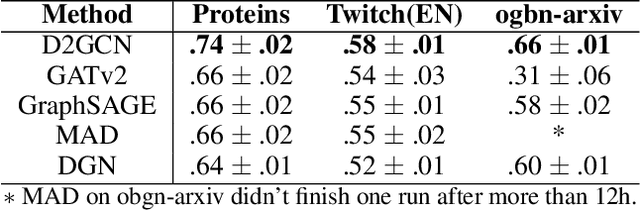
Graph Convolutional Neural Networks (GCNs) has been generally accepted to be an effective tool for node representations learning. An interesting way to understand GCNs is to think of them as a message passing mechanism where each node updates its representation by accepting information from its neighbours (also known as positive samples). However, beyond these neighbouring nodes, graphs have a large, dark, all-but forgotten world in which we find the non-neighbouring nodes (negative samples). In this paper, we show that this great dark world holds a substantial amount of information that might be useful for representation learning. Most specifically, it can provide negative information about the node representations. Our overall idea is to select appropriate negative samples for each node and incorporate the negative information contained in these samples into the representation updates. Moreover, we show that the process of selecting the negative samples is not trivial. Our theme therefore begins by describing the criteria for a good negative sample, followed by a determinantal point process algorithm for efficiently obtaining such samples. A GCN, boosted by diverse negative samples, then jointly considers the positive and negative information when passing messages. Experimental evaluations show that this idea not only improves the overall performance of standard representation learning but also significantly alleviates over-smoothing problems.

Repulsive Mixture Models of Exponential Family PCA for Clustering

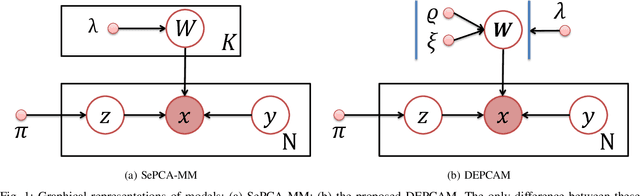
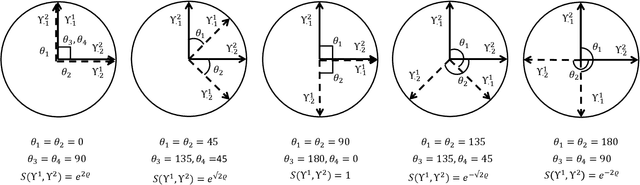
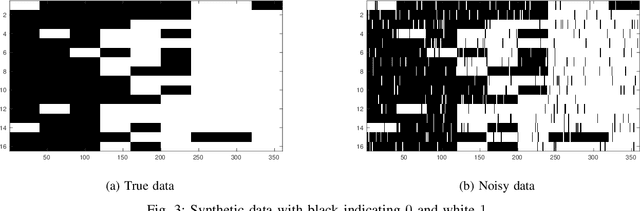
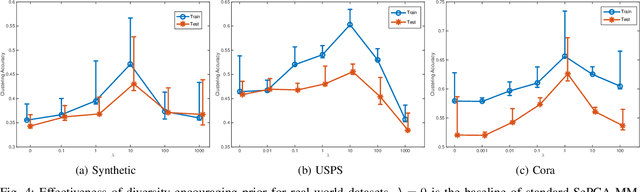
The mixture extension of exponential family principal component analysis (EPCA) was designed to encode much more structural information about data distribution than the traditional EPCA does. For example, due to the linearity of EPCA's essential form, nonlinear cluster structures cannot be easily handled, but they are explicitly modeled by the mixing extensions. However, the traditional mixture of local EPCAs has the problem of model redundancy, i.e., overlaps among mixing components, which may cause ambiguity for data clustering. To alleviate this problem, in this paper, a repulsiveness-encouraging prior is introduced among mixing components and a diversified EPCA mixture (DEPCAM) model is developed in the Bayesian framework. Specifically, a determinantal point process (DPP) is exploited as a diversity-encouraging prior distribution over the joint local EPCAs. As required, a matrix-valued measure for L-ensemble kernel is designed, within which, $\ell_1$ constraints are imposed to facilitate selecting effective PCs of local EPCAs, and angular based similarity measure are proposed. An efficient variational EM algorithm is derived to perform parameter learning and hidden variable inference. Experimental results on both synthetic and real-world datasets confirm the effectiveness of the proposed method in terms of model parsimony and generalization ability on unseen test data.

Detecting Communities in Heterogeneous Multi-Relational Networks:A Message Passing based Approach

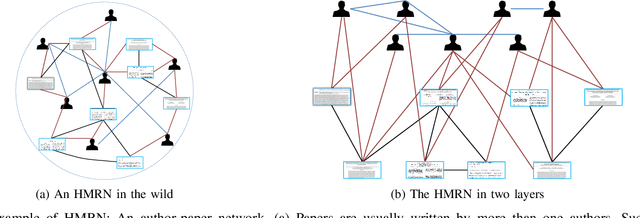
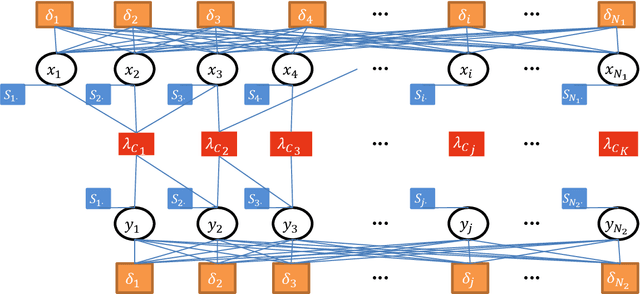
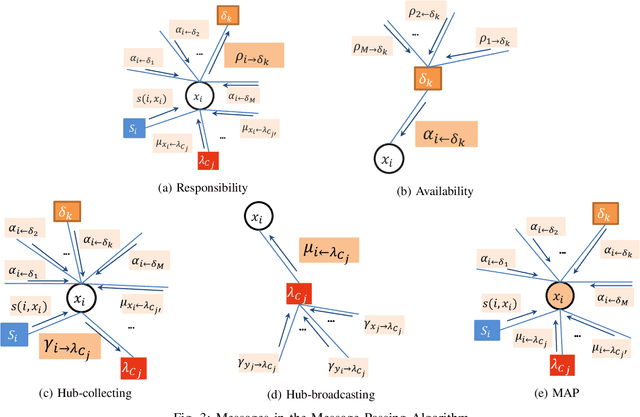
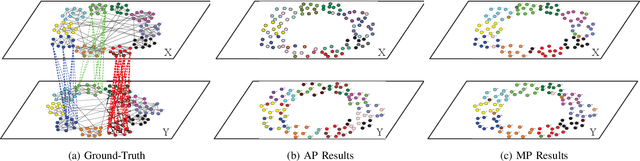
Community is a common characteristic of networks including social networks, biological networks, computer and information networks, to name a few. Community detection is a basic step for exploring and analysing these network data. Typically, homogenous network is a type of networks which consists of only one type of objects with one type of links connecting them. There has been a large body of developments in models and algorithms to detect communities over it. However, real-world networks naturally exhibit heterogeneous qualities appearing as multiple types of objects with multi-relational links connecting them. Those heterogeneous information could facilitate the community detection for its constituent homogeneous networks, but has not been fully explored. In this paper, we exploit heterogeneous multi-relational networks (HMRNet) and propose an efficient message passing based algorithm to simultaneously detect communities for all homogeneous networks. Specifically, an HMRNet is reorganized into a hierarchical structure with homogeneous networks as its layers and heterogeneous links connecting them. To detect communities in such an HMRNet, the problem is formulated as a maximum a posterior (MAP) over a factor graph. Finally a message passing based algorithm is derived to find a best solution of the MAP problem. Evaluation on both synthetic and real-world networks confirms the effectiveness of the proposed method.

Diversified Hidden Markov Models for Sequential Labeling

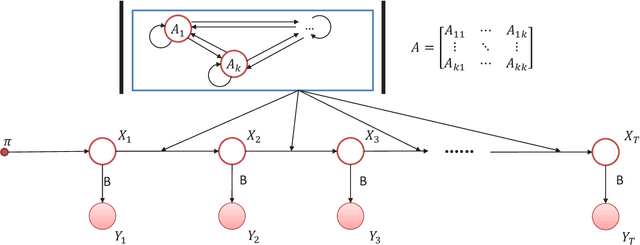
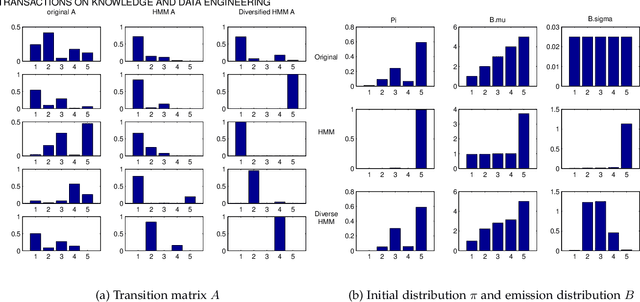
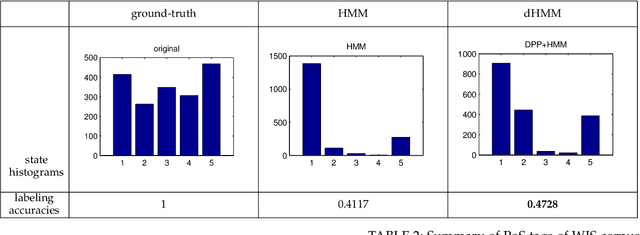
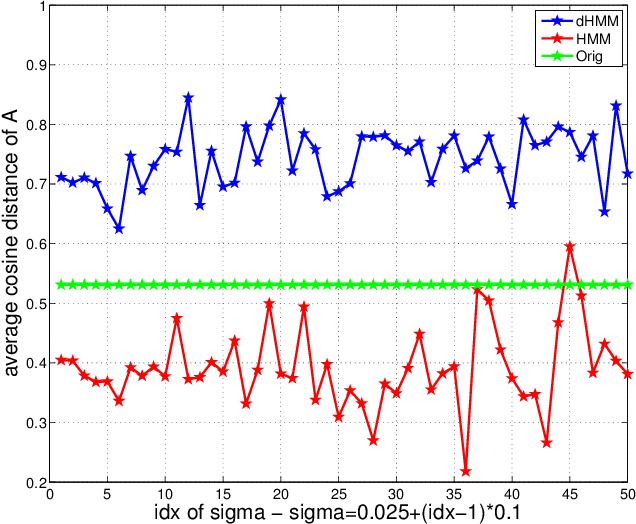
Labeling of sequential data is a prevalent meta-problem for a wide range of real world applications. While the first-order Hidden Markov Models (HMM) provides a fundamental approach for unsupervised sequential labeling, the basic model does not show satisfying performance when it is directly applied to real world problems, such as part-of-speech tagging (PoS tagging) and optical character recognition (OCR). Aiming at improving performance, important extensions of HMM have been proposed in the literatures. One of the common key features in these extensions is the incorporation of proper prior information. In this paper, we propose a new extension of HMM, termed diversified Hidden Markov Models (dHMM), which utilizes a diversity-encouraging prior over the state-transition probabilities and thus facilitates more dynamic sequential labellings. Specifically, the diversity is modeled by a continuous determinantal point process prior, which we apply to both unsupervised and supervised scenarios. Learning and inference algorithms for dHMM are derived. Empirical evaluations on benchmark datasets for unsupervised PoS tagging and supervised OCR confirmed the effectiveness of dHMM, with competitive performance to the state-of-the-art.

Adapting Stochastic Block Models to Power-Law Degree Distributions

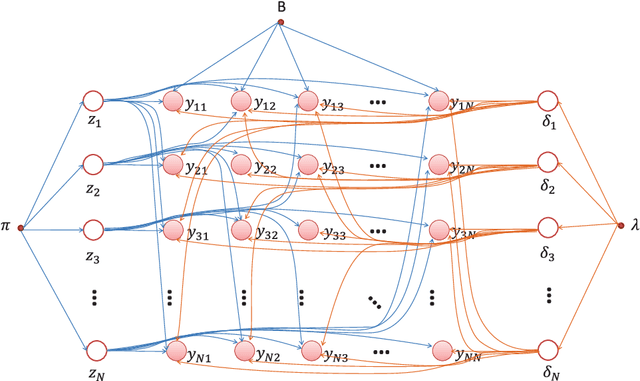
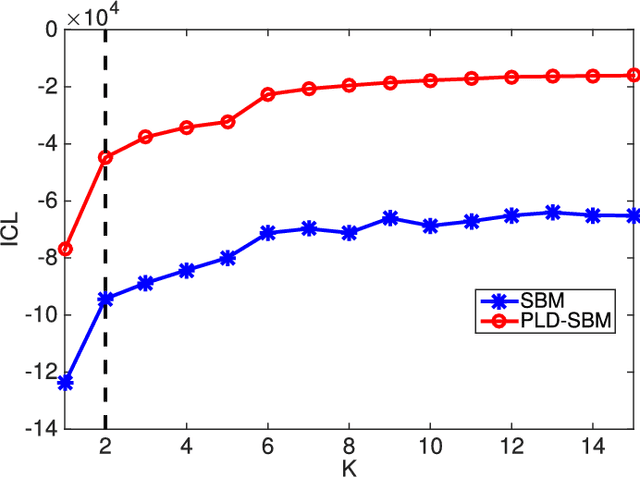
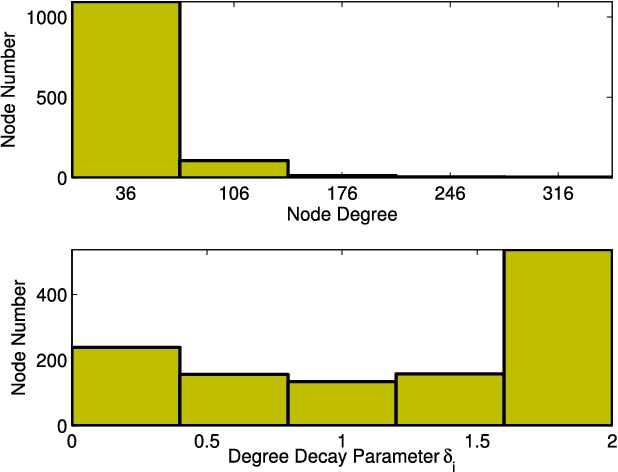
Stochastic block models (SBMs) have been playing an important role in modeling clusters or community structures of network data. But, it is incapable of handling several complex features ubiquitously exhibited in real-world networks, one of which is the power-law degree characteristic. To this end, we propose a new variant of SBM, termed power-law degree SBM (PLD-SBM), by introducing degree decay variables to explicitly encode the varying degree distribution over all nodes. With an exponential prior, it is proved that PLD-SBM approximately preserves the scale-free feature in real networks. In addition, from the inference of variational E-Step, PLD-SBM is indeed to correct the bias inherited in SBM with the introduced degree decay factors. Furthermore, experiments conducted on both synthetic networks and two real-world datasets including Adolescent Health Data and the political blogs network verify the effectiveness of the proposed model in terms of cluster prediction accuracies.