Demystify Self-Attention in Vision Transformers from a Semantic Perspective: Analysis and Application

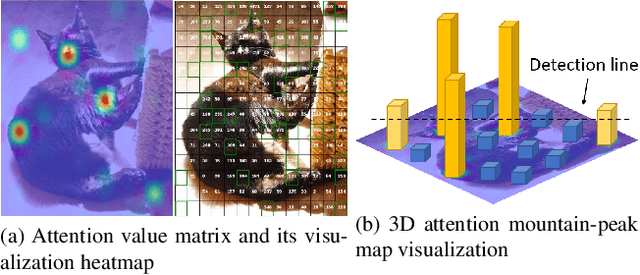
Self-attention mechanisms, especially multi-head self-attention (MSA), have achieved great success in many fields such as computer vision and natural language processing. However, many existing vision transformer (ViT) works simply inherent transformer designs from NLP to adapt vision tasks, while ignoring the fundamental difference between ``how MSA works in image and language settings''. Language naturally contains highly semantic structures that are directly interpretable by humans. Its basic unit (word) is discrete without redundant information, which readily supports interpretable studies on MSA mechanisms of language transformer. In contrast, visual data exhibits a fundamentally different structure: Its basic unit (pixel) is a natural low-level representation with significant redundancies in the neighbourhood, which poses obvious challenges to the interpretability of MSA mechanism in ViT. In this paper, we introduce a typical image processing technique, i.e., scale-invariant feature transforms (SIFTs), which maps low-level representations into mid-level spaces, and annotates extensive discrete keypoints with semantically rich information. Next, we construct a weighted patch interrelation analysis based on SIFT keypoints to capture the attention patterns hidden in patches with different semantic concentrations Interestingly, we find this quantitative analysis is not only an effective complement to the interpretability of MSA mechanisms in ViT, but can also be applied to 1) spurious correlation discovery and ``prompting'' during model inference, 2) and guided model pre-training acceleration. Experimental results on both applications show significant advantages over baselines, demonstrating the efficacy of our method.

Diversified Hidden Markov Models for Sequential Labeling

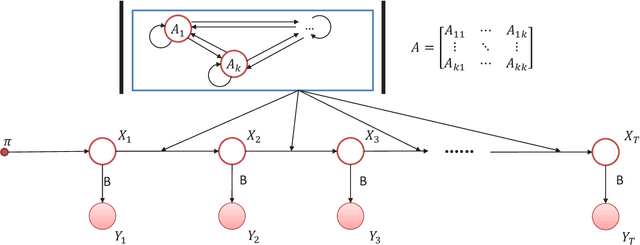
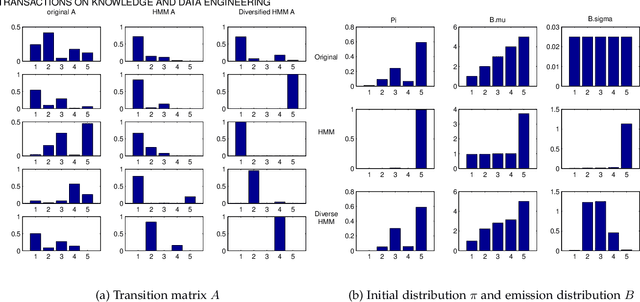
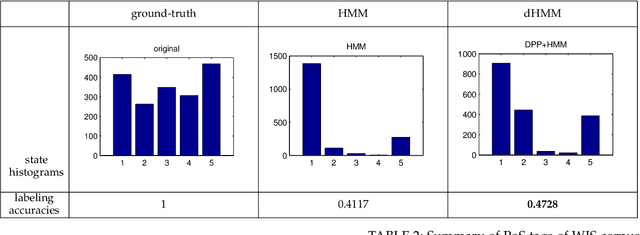
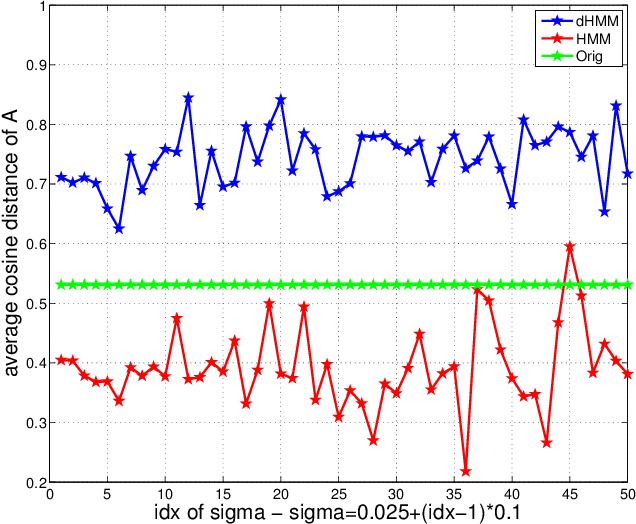
Labeling of sequential data is a prevalent meta-problem for a wide range of real world applications. While the first-order Hidden Markov Models (HMM) provides a fundamental approach for unsupervised sequential labeling, the basic model does not show satisfying performance when it is directly applied to real world problems, such as part-of-speech tagging (PoS tagging) and optical character recognition (OCR). Aiming at improving performance, important extensions of HMM have been proposed in the literatures. One of the common key features in these extensions is the incorporation of proper prior information. In this paper, we propose a new extension of HMM, termed diversified Hidden Markov Models (dHMM), which utilizes a diversity-encouraging prior over the state-transition probabilities and thus facilitates more dynamic sequential labellings. Specifically, the diversity is modeled by a continuous determinantal point process prior, which we apply to both unsupervised and supervised scenarios. Learning and inference algorithms for dHMM are derived. Empirical evaluations on benchmark datasets for unsupervised PoS tagging and supervised OCR confirmed the effectiveness of dHMM, with competitive performance to the state-of-the-art.

Relative Pairwise Relationship Constrained Non-negative Matrix Factorisation

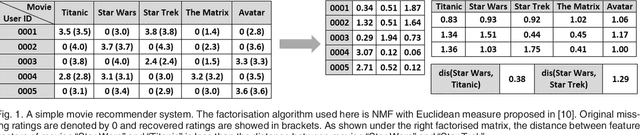
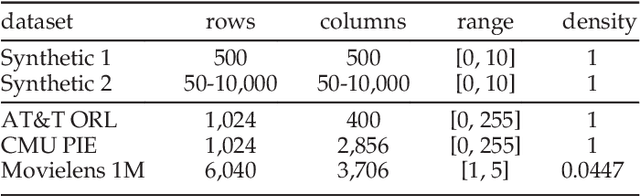
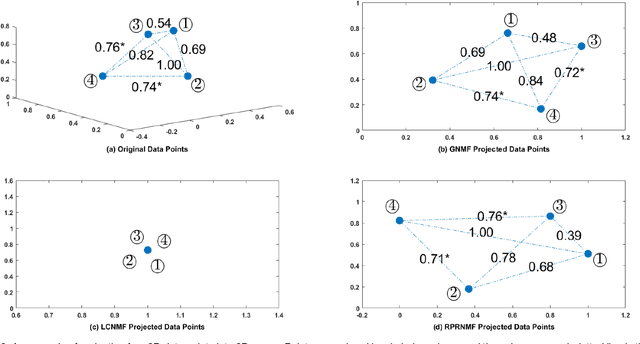
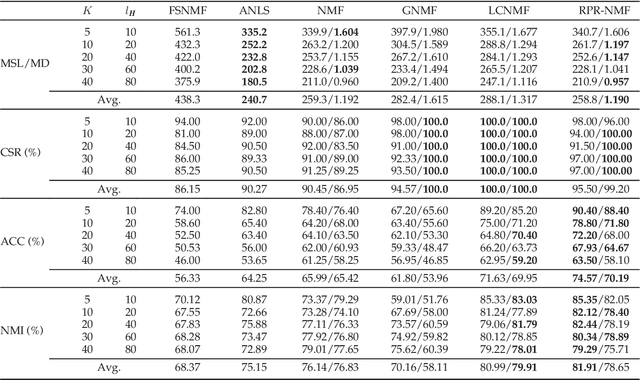
Non-negative Matrix Factorisation (NMF) has been extensively used in machine learning and data analytics applications. Most existing variations of NMF only consider how each row/column vector of factorised matrices should be shaped, and ignore the relationship among pairwise rows or columns. In many cases, such pairwise relationship enables better factorisation, for example, image clustering and recommender systems. In this paper, we propose an algorithm named, Relative Pairwise Relationship constrained Non-negative Matrix Factorisation (RPR-NMF), which places constraints over relative pairwise distances amongst features by imposing penalties in a triplet form. Two distance measures, squared Euclidean distance and Symmetric divergence, are used, and exponential and hinge loss penalties are adopted for the two measures respectively. It is well known that the so-called "multiplicative update rules" result in a much faster convergence than gradient descend for matrix factorisation. However, applying such update rules to RPR-NMF and also proving its convergence is not straightforward. Thus, we use reasonable approximations to relax the complexity brought by the penalties, which are practically verified. Experiments on both synthetic datasets and real datasets demonstrate that our algorithms have advantages on gaining close approximation, satisfying a high proportion of expected constraints, and achieving superior performance compared with other algorithms.