Ben Liao
Kim
MolHF: A Hierarchical Normalizing Flow for Molecular Graph Generation
May 15, 2023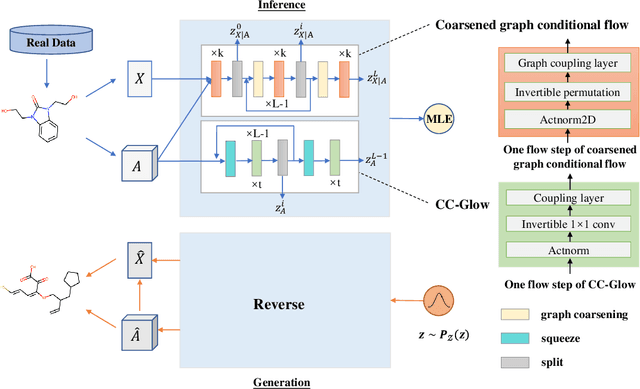
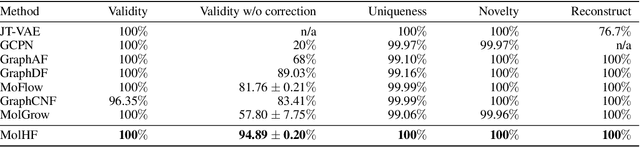
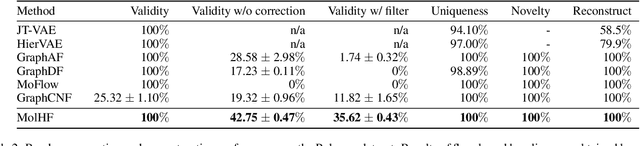
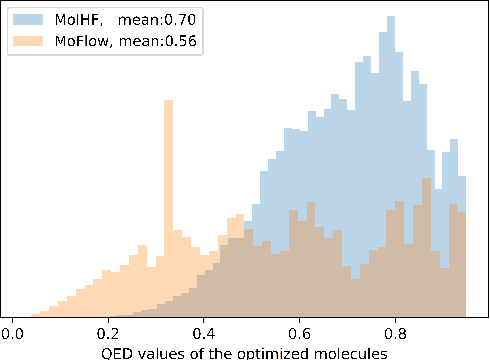
Abstract:Molecular de novo design is a critical yet challenging task in scientific fields, aiming to design novel molecular structures with desired property profiles. Significant progress has been made by resorting to generative models for graphs. However, limited attention is paid to hierarchical generative models, which can exploit the inherent hierarchical structure (with rich semantic information) of the molecular graphs and generate complex molecules of larger size that we shall demonstrate to be difficult for most existing models. The primary challenge to hierarchical generation is the non-differentiable issue caused by the generation of intermediate discrete coarsened graph structures. To sidestep this issue, we cast the tricky hierarchical generation problem over discrete spaces as the reverse process of hierarchical representation learning and propose MolHF, a new hierarchical flow-based model that generates molecular graphs in a coarse-to-fine manner. Specifically, MolHF first generates bonds through a multi-scale architecture, then generates atoms based on the coarsened graph structure at each scale. We demonstrate that MolHF achieves state-of-the-art performance in random generation and property optimization, implying its high capacity to model data distribution. Furthermore, MolHF is the first flow-based model that can be applied to model larger molecules (polymer) with more than 100 heavy atoms. The code and models are available at https://github.com/violet-sto/MolHF.
Learning Large-scale Network Embedding from Representative Subgraph
Dec 02, 2021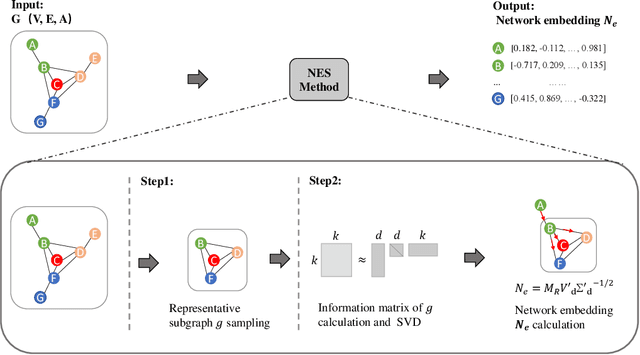
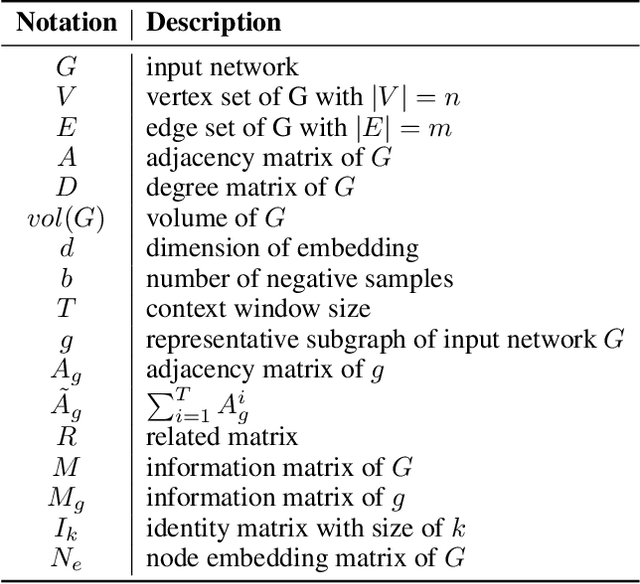
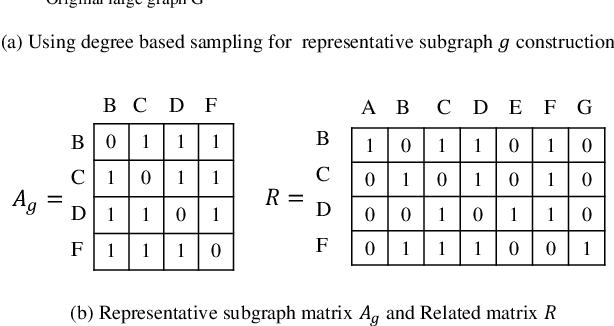
Abstract:We study the problem of large-scale network embedding, which aims to learn low-dimensional latent representations for network mining applications. Recent research in the field of network embedding has led to significant progress such as DeepWalk, LINE, NetMF, NetSMF. However, the huge size of many real-world networks makes it computationally expensive to learn network embedding from the entire network. In this work, we present a novel network embedding method called "NES", which learns network embedding from a small representative subgraph. NES leverages theories from graph sampling to efficiently construct representative subgraph with smaller size which can be used to make inferences about the full network, enabling significantly improved efficiency in embedding learning. Then, NES computes the network embedding from this representative subgraph, efficiently. Compared with well-known methods, extensive experiments on networks of various scales and types demonstrate that NES achieves comparable performance and significant efficiency superiority.
Fast Extraction of Word Embedding from Q-contexts
Sep 15, 2021
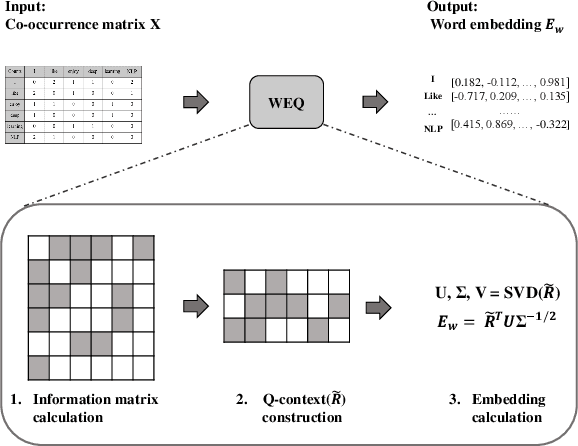
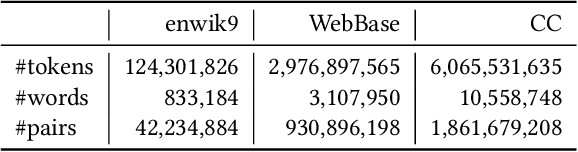
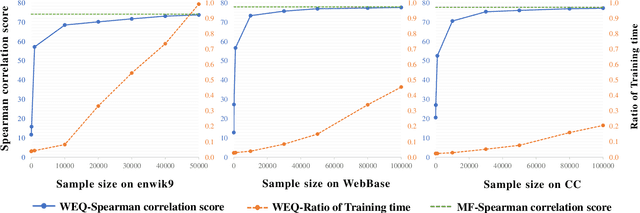
Abstract:The notion of word embedding plays a fundamental role in natural language processing (NLP). However, pre-training word embedding for very large-scale vocabulary is computationally challenging for most existing methods. In this work, we show that with merely a small fraction of contexts (Q-contexts)which are typical in the whole corpus (and their mutual information with words), one can construct high-quality word embedding with negligible errors. Mutual information between contexts and words can be encoded canonically as a sampling state, thus, Q-contexts can be fast constructed. Furthermore, we present an efficient and effective WEQ method, which is capable of extracting word embedding directly from these typical contexts. In practical scenarios, our algorithm runs 11$\sim$13 times faster than well-established methods. By comparing with well-known methods such as matrix factorization, word2vec, GloVeand fasttext, we demonstrate that our method achieves comparable performance on a variety of downstream NLP tasks, and in the meanwhile maintains run-time and resource advantages over all these baselines.
Balancing Accuracy and Fairness for Interactive Recommendation with Reinforcement Learning
Jun 25, 2021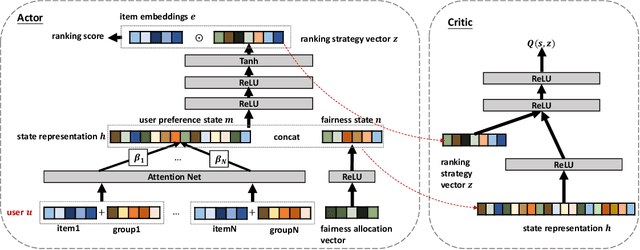
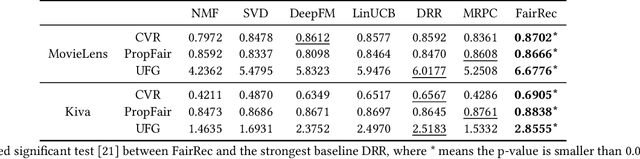
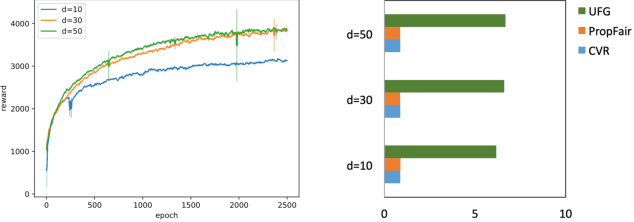
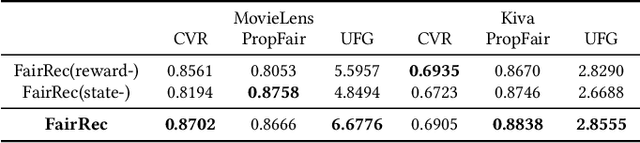
Abstract:Fairness in recommendation has attracted increasing attention due to bias and discrimination possibly caused by traditional recommenders. In Interactive Recommender Systems (IRS), user preferences and the system's fairness status are constantly changing over time. Existing fairness-aware recommenders mainly consider fairness in static settings. Directly applying existing methods to IRS will result in poor recommendation. To resolve this problem, we propose a reinforcement learning based framework, FairRec, to dynamically maintain a long-term balance between accuracy and fairness in IRS. User preferences and the system's fairness status are jointly compressed into the state representation to generate recommendations. FairRec aims at maximizing our designed cumulative reward that combines accuracy and fairness. Extensive experiments validate that FairRec can improve fairness, while preserving good recommendation quality.
Concentration Bounds for Co-occurrence Matrices of Markov Chains
Aug 06, 2020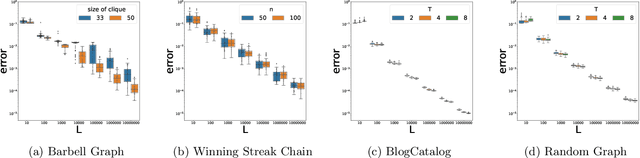
Abstract:Co-occurrence statistics for sequential data are common and important data signals in machine learning, which provide rich correlation and clustering information about the underlying object space. We give the first bound on the convergence rate of estimating the co-occurrence matrix of a regular (aperiodic and irreducible) finite Markov chain from a single random trajectory. Our work is motivated by the analysis of a well-known graph learning algorithm DeepWalk by [Qiu et al. WSDM '18], who study the convergence (in probability) of co-occurrence matrix from random walk on undirected graphs in the limit, but left the convergence rate an open problem. We prove a Chernoff-type bound for sums of matrix-valued random variables sampled via an ergodic Markov chain, generalizing the regular undirected graph case studied by [Garg et al. STOC '18]. Using the Chernoff-type bound, we show that given a regular Markov chain with $n$ states and mixing time $\tau$, we need a trajectory of length $O(\tau (\log{(n)}+\log{(\tau)})/\epsilon^2)$ to achieve an estimator of the co-occurrence matrix with error bound $\epsilon$. We conduct several experiments and the experimental results are consistent with the exponentially fast convergence rate from theoretical analysis. Our result gives the first sample complexity analysis in graph representation learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge