Vulnerability of Text-Matching in ML/AI Conference Reviewer Assignments to Collusions

In the peer review process of top-tier machine learning (ML) and artificial intelligence (AI) conferences, reviewers are assigned to papers through automated methods. These assignment algorithms consider two main factors: (1) reviewers' expressed interests indicated by their bids for papers, and (2) reviewers' domain expertise inferred from the similarity between the text of their previously published papers and the submitted manuscripts. A significant challenge these conferences face is the existence of collusion rings, where groups of researchers manipulate the assignment process to review each other's papers, providing positive evaluations regardless of their actual quality. Most efforts to combat collusion rings have focused on preventing bid manipulation, under the assumption that the text similarity component is secure. In this paper, we demonstrate that even in the absence of bidding, colluding reviewers and authors can exploit the machine learning based text-matching component of reviewer assignment used at top ML/AI venues to get assigned their target paper. We also highlight specific vulnerabilities within this system and offer suggestions to enhance its robustness.

Learning Large-scale Network Embedding from Representative Subgraph

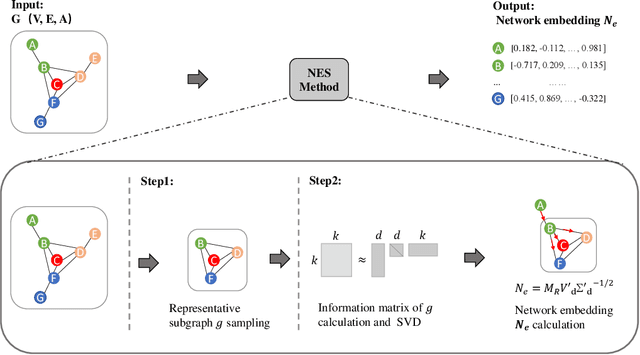
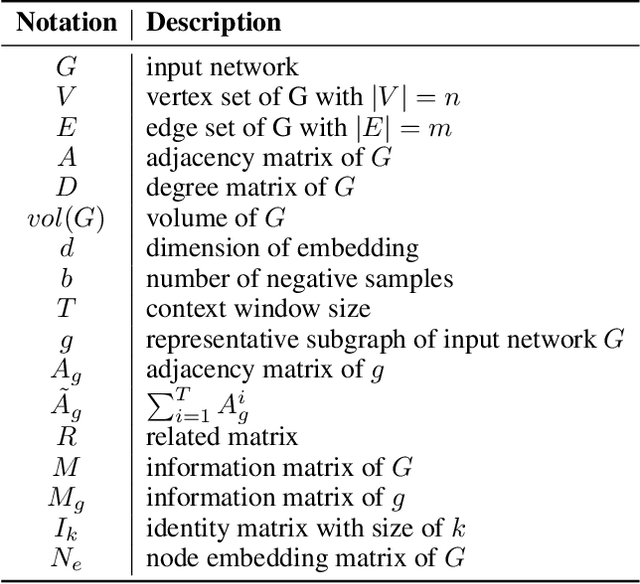
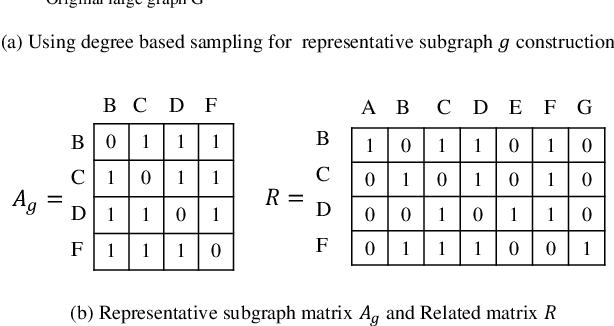
We study the problem of large-scale network embedding, which aims to learn low-dimensional latent representations for network mining applications. Recent research in the field of network embedding has led to significant progress such as DeepWalk, LINE, NetMF, NetSMF. However, the huge size of many real-world networks makes it computationally expensive to learn network embedding from the entire network. In this work, we present a novel network embedding method called "NES", which learns network embedding from a small representative subgraph. NES leverages theories from graph sampling to efficiently construct representative subgraph with smaller size which can be used to make inferences about the full network, enabling significantly improved efficiency in embedding learning. Then, NES computes the network embedding from this representative subgraph, efficiently. Compared with well-known methods, extensive experiments on networks of various scales and types demonstrate that NES achieves comparable performance and significant efficiency superiority.

Overcoming Catastrophic Forgetting by Generative Regularization

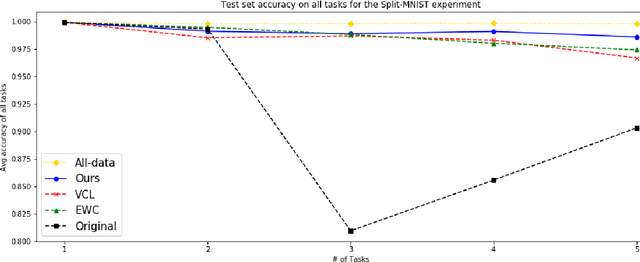
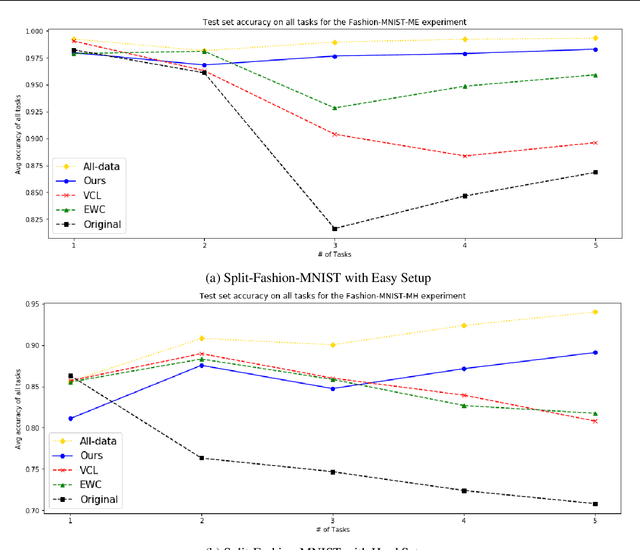
In this paper, we propose a new method to overcome catastrophic forgetting by adding generative regularization to Bayesian inference framework. We could construct generative regularization term for all given models by leveraging Energy-based models and Langevin-Dynamic sampling. By combining discriminative and generative loss together, we show that this intuitively provides a better posterior formulation in Bayesian inference. Experimental results show that the proposed method outperforms state of-the-art methods on a variety of tasks, avoiding catastrophic forgetting in continual learning. In particular, the proposed method outperforms previous methos over 10$\%$ in Fashion-MNIST dataset.