Beilun Wang
Structured Episodic Event Memory
Jan 10, 2026Abstract:Current approaches to memory in Large Language Models (LLMs) predominantly rely on static Retrieval-Augmented Generation (RAG), which often results in scattered retrieval and fails to capture the structural dependencies required for complex reasoning. For autonomous agents, these passive and flat architectures lack the cognitive organization necessary to model the dynamic and associative nature of long-term interaction. To address this, we propose Structured Episodic Event Memory (SEEM), a hierarchical framework that synergizes a graph memory layer for relational facts with a dynamic episodic memory layer for narrative progression. Grounded in cognitive frame theory, SEEM transforms interaction streams into structured Episodic Event Frames (EEFs) anchored by precise provenance pointers. Furthermore, we introduce an agentic associative fusion and Reverse Provenance Expansion (RPE) mechanism to reconstruct coherent narrative contexts from fragmented evidence. Experimental results on the LoCoMo and LongMemEval benchmarks demonstrate that SEEM significantly outperforms baselines, enabling agents to maintain superior narrative coherence and logical consistency.
MolAct: An Agentic RL Framework for Molecular Editing and Property Optimization
Dec 24, 2025Abstract:Molecular editing and optimization are multi-step problems that require iteratively improving properties while keeping molecules chemically valid and structurally similar. We frame both tasks as sequential, tool-guided decisions and introduce MolAct, an agentic reinforcement learning framework that employs a two-stage training paradigm: first building editing capability, then optimizing properties while reusing the learned editing behaviors. To the best of our knowledge, this is the first work to formalize molecular design as an Agentic Reinforcement Learning problem, where an LLM agent learns to interleave reasoning, tool-use, and molecular optimization. The framework enables agents to interact in multiple turns, invoking chemical tools for validity checking, property assessment, and similarity control, and leverages their feedback to refine subsequent edits. We instantiate the MolAct framework to train two model families: MolEditAgent for molecular editing tasks and MolOptAgent for molecular optimization tasks. In molecular editing, MolEditAgent-7B delivers 100, 95, and 98 valid add, delete, and substitute edits, outperforming strong closed "thinking" baselines such as DeepSeek-R1; MolEditAgent-3B approaches the performance of much larger open "thinking" models like Qwen3-32B-think. In molecular optimization, MolOptAgent-7B (trained on MolEditAgent-7B) surpasses the best closed "thinking" baseline (e.g., Claude 3.7) on LogP and remains competitive on solubility, while maintaining balanced performance across other objectives. These results highlight that treating molecular design as a multi-step, tool-augmented process is key to reliable and interpretable improvements.
ILIF: Temporal Inhibitory Leaky Integrate-and-Fire Neuron for Overactivation in Spiking Neural Networks
May 15, 2025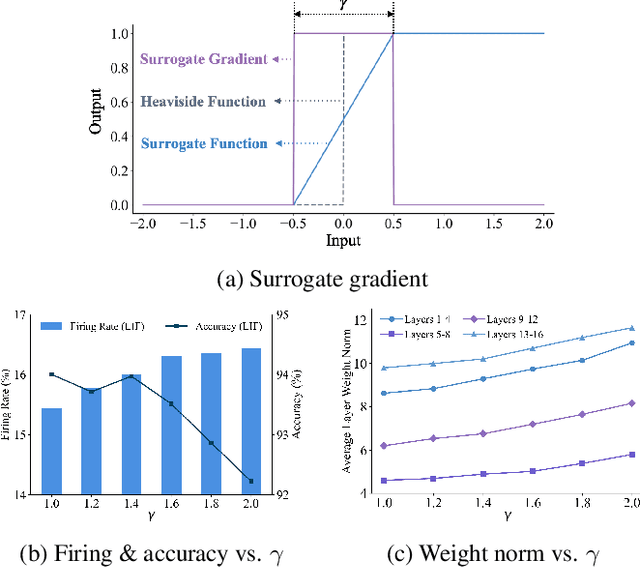
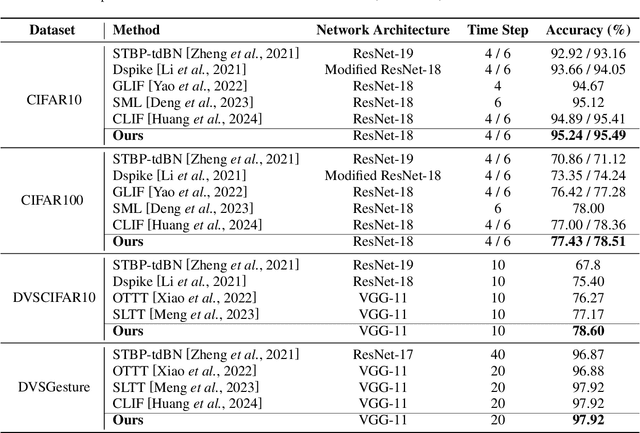
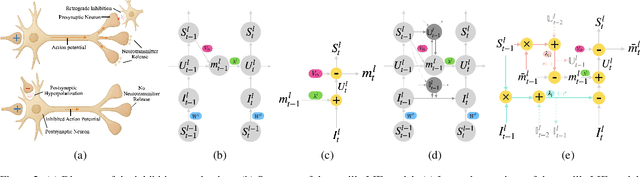

Abstract:The Spiking Neural Network (SNN) has drawn increasing attention for its energy-efficient, event-driven processing and biological plausibility. To train SNNs via backpropagation, surrogate gradients are used to approximate the non-differentiable spike function, but they only maintain nonzero derivatives within a narrow range of membrane potentials near the firing threshold, referred to as the surrogate gradient support width gamma. We identify a major challenge, termed the dilemma of gamma: a relatively large gamma leads to overactivation, characterized by excessive neuron firing, which in turn increases energy consumption, whereas a small gamma causes vanishing gradients and weakens temporal dependencies. To address this, we propose a temporal Inhibitory Leaky Integrate-and-Fire (ILIF) neuron model, inspired by biological inhibitory mechanisms. This model incorporates interconnected inhibitory units for membrane potential and current, effectively mitigating overactivation while preserving gradient propagation. Theoretical analysis demonstrates ILIF effectiveness in overcoming the gamma dilemma, and extensive experiments on multiple datasets show that ILIF improves energy efficiency by reducing firing rates, stabilizes training, and enhances accuracy. The code is available at github.com/kaisun1/ILIF.
Label Information Enhanced Fraud Detection against Low Homophily in Graphs
Feb 21, 2023



Abstract:Node classification is a substantial problem in graph-based fraud detection. Many existing works adopt Graph Neural Networks (GNNs) to enhance fraud detectors. While promising, currently most GNN-based fraud detectors fail to generalize to the low homophily setting. Besides, label utilization has been proved to be significant factor for node classification problem. But we find they are less effective in fraud detection tasks due to the low homophily in graphs. In this work, we propose GAGA, a novel Group AGgregation enhanced TrAnsformer, to tackle the above challenges. Specifically, the group aggregation provides a portable method to cope with the low homophily issue. Such an aggregation explicitly integrates the label information to generate distinguishable neighborhood information. Along with group aggregation, an attempt towards end-to-end trainable group encoding is proposed which augments the original feature space with the class labels. Meanwhile, we devise two additional learnable encodings to recognize the structural and relational context. Then, we combine the group aggregation and the learnable encodings into a Transformer encoder to capture the semantic information. Experimental results clearly show that GAGA outperforms other competitive graph-based fraud detectors by up to 24.39% on two trending public datasets and a real-world industrial dataset from Anonymous. Even more, the group aggregation is demonstrated to outperform other label utilization methods (e.g., C&S, BoT/UniMP) in the low homophily setting.
Differential Network Learning Beyond Data Samples
Apr 24, 2020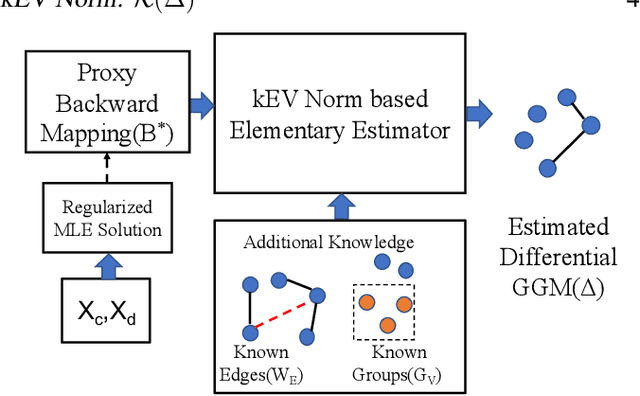
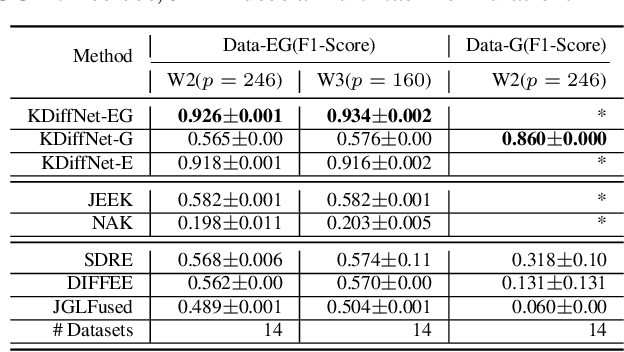
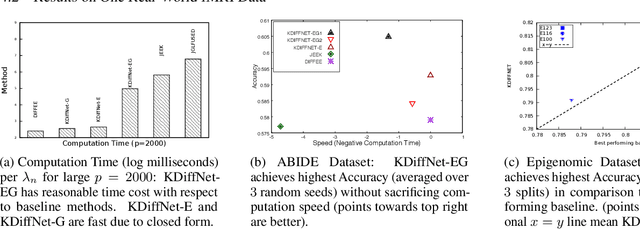
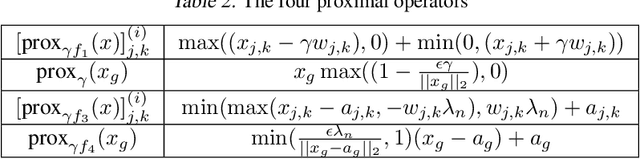
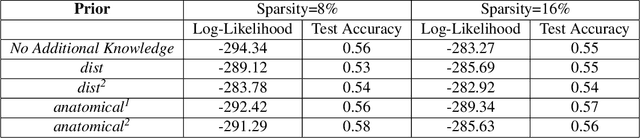
Abstract:Learning the change of statistical dependencies between random variables is an essential task for many real-life applications, mostly in the high dimensional low sample regime. In this paper, we propose a novel differential parameter estimator that, in comparison to current methods, simultaneously allows (a) the flexible integration of multiple sources of information (data samples, variable groupings, extra pairwise evidence, etc.), (b) being scalable to a large number of variables, and (c) achieving a sharp asymptotic convergence rate. Our experiments, on more than 100 simulated and two real-world datasets, validate the flexibility of our approach and highlight the benefits of integrating spatial and anatomic information for brain connectome change discovery and epigenetic network identification.
Fast and Scalable Estimator for Sparse and Unit-Rank Higher-Order Regression Models
Nov 29, 2019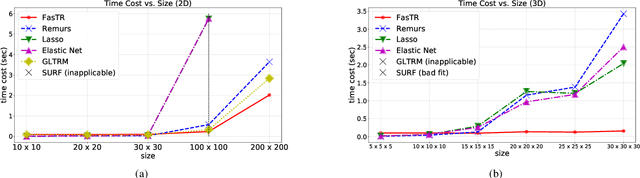
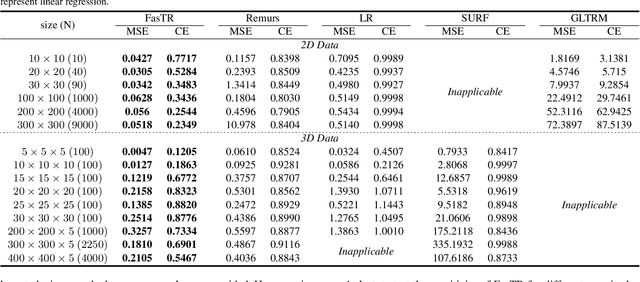
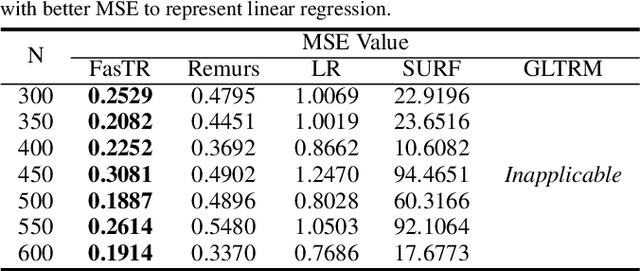
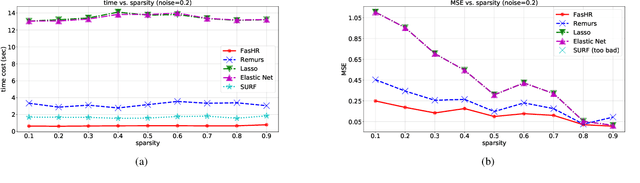
Abstract:Because tensor data appear more and more frequently in various scientific researches and real-world applications, analyzing the relationship between tensor features and the univariate outcome becomes an elementary task in many fields. To solve this task, we propose \underline{Fa}st \underline{S}parse \underline{T}ensor \underline{R}egression model (FasTR) based on so-called unit-rank CANDECOMP/PARAFAC decomposition. FasTR first decomposes the tensor coefficient into component vectors and then estimates each vector with $\ell_1$ regularized regression. Because of the independence of component vectors, FasTR is able to solve in a parallel way and the time complexity is proved to be superior to previous models. We evaluate the performance of FasTR on several simulated datasets and a real-world fMRI dataset. Experiment results show that, compared with four baseline models, in every case, FasTR can compute a better solution within less time.
Sparse and Low-Rank Tensor Regression via Parallel Proximal Method
Nov 29, 2019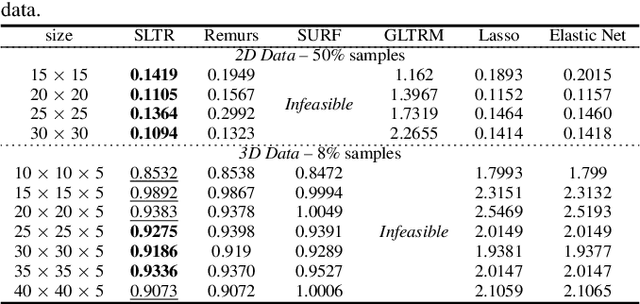
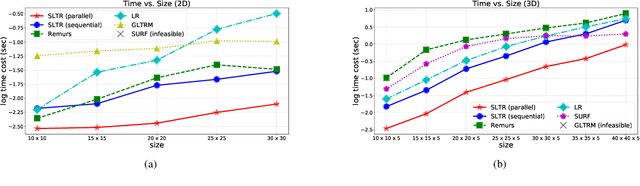
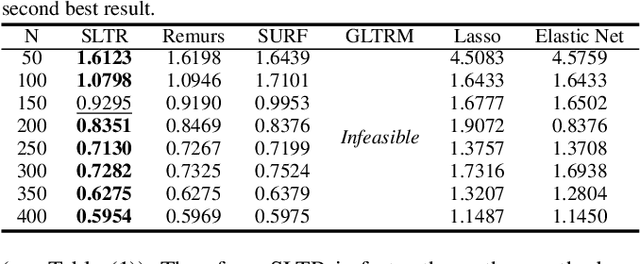
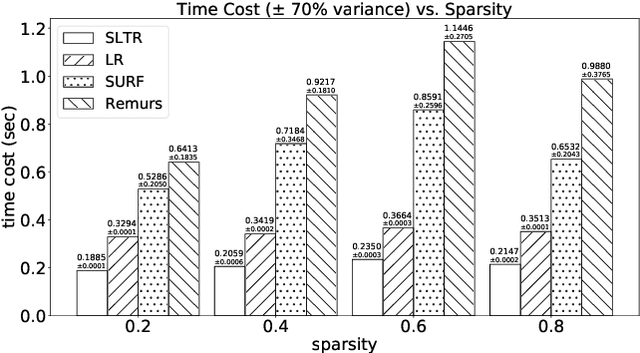
Abstract:Motivated by applications in various scientific fields having demand of predicting relationship between higher-order (tensor) feature and univariate response, we propose a \underline{S}parse and \underline{L}ow-rank \underline{T}ensor \underline{R}egression model (SLTR). This model enforces sparsity and low-rankness of the tensor coefficient by directly applying $\ell_1$ norm and tensor nuclear norm on it respectively, such that (1) the structural information of tensor is preserved and (2) the data interpretation is convenient. To make the solving procedure scalable and efficient, SLTR makes use of the proximal gradient method to optimize two norm regularizers, which can be easily implemented parallelly. Additionally, a tighter convergence rate is proved over three-order tensor data. We evaluate SLTR on several simulated datasets and one fMRI dataset. Experiment results show that, compared with previous models, SLTR is able to obtain a solution no worse than others with much less time cost.
A Fast and Scalable Joint Estimator for Integrating Additional Knowledge in Learning Multiple Related Sparse Gaussian Graphical Models
Jul 17, 2018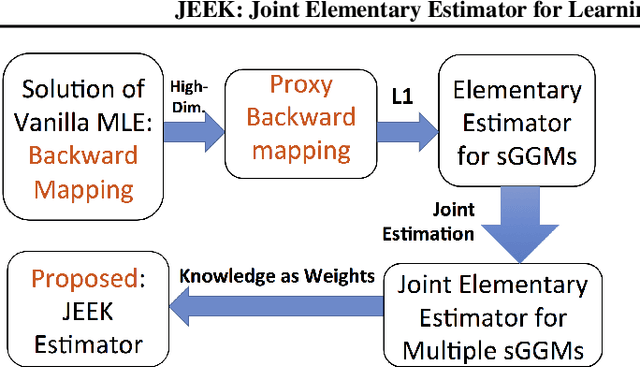

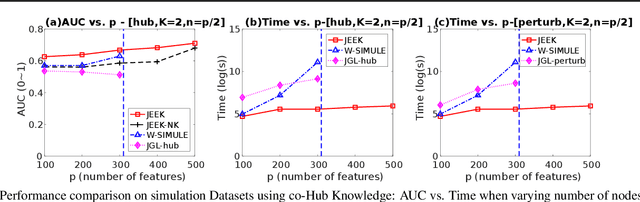
Abstract:We consider the problem of including additional knowledge in estimating sparse Gaussian graphical models (sGGMs) from aggregated samples, arising often in bioinformatics and neuroimaging applications. Previous joint sGGM estimators either fail to use existing knowledge or cannot scale-up to many tasks (large $K$) under a high-dimensional (large $p$) situation. In this paper, we propose a novel \underline{J}oint \underline{E}lementary \underline{E}stimator incorporating additional \underline{K}nowledge (JEEK) to infer multiple related sparse Gaussian Graphical models from large-scale heterogeneous data. Using domain knowledge as weights, we design a novel hybrid norm as the minimization objective to enforce the superposition of two weighted sparsity constraints, one on the shared interactions and the other on the task-specific structural patterns. This enables JEEK to elegantly consider various forms of existing knowledge based on the domain at hand and avoid the need to design knowledge-specific optimization. JEEK is solved through a fast and entry-wise parallelizable solution that largely improves the computational efficiency of the state-of-the-art $O(p^5K^4)$ to $O(p^2K^4)$. We conduct a rigorous statistical analysis showing that JEEK achieves the same convergence rate $O(\log(Kp)/n_{tot})$ as the state-of-the-art estimators that are much harder to compute. Empirically, on multiple synthetic datasets and two real-world data, JEEK outperforms the speed of the state-of-arts significantly while achieving the same level of prediction accuracy. Available as R tool "jeek"
Fast and Scalable Learning of Sparse Changes in High-Dimensional Gaussian Graphical Model Structure
May 23, 2018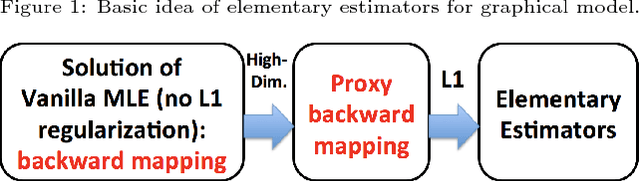
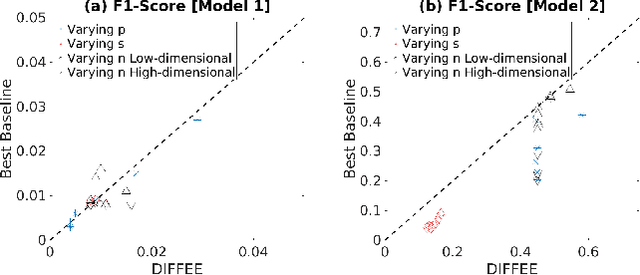
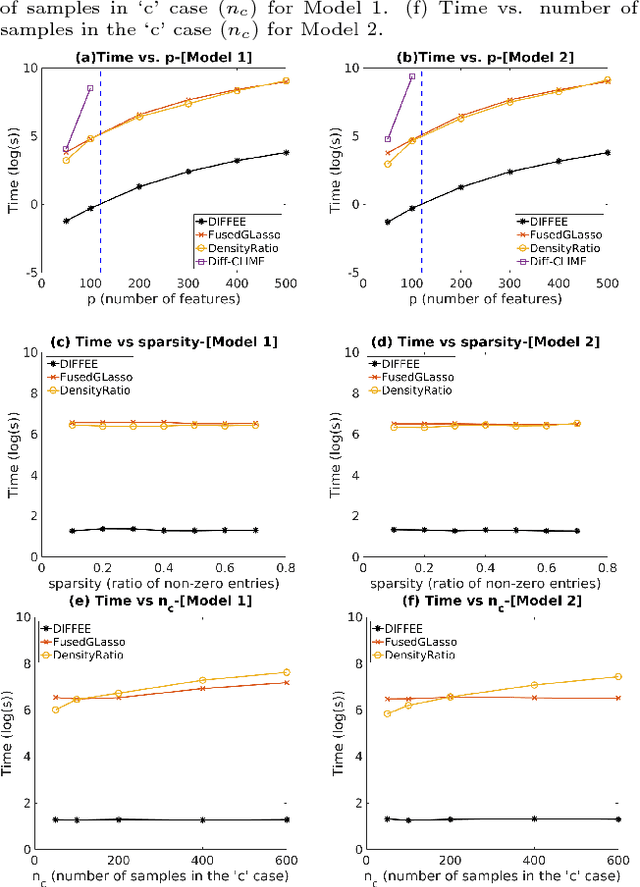
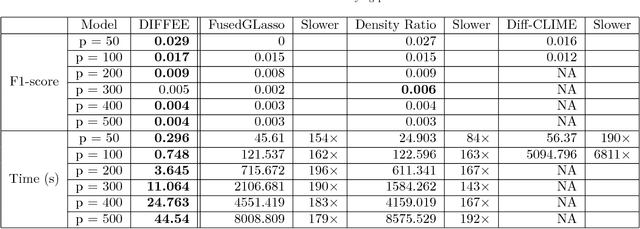
Abstract:We focus on the problem of estimating the change in the dependency structures of two $p$-dimensional Gaussian Graphical models (GGMs). Previous studies for sparse change estimation in GGMs involve expensive and difficult non-smooth optimization. We propose a novel method, DIFFEE for estimating DIFFerential networks via an Elementary Estimator under a high-dimensional situation. DIFFEE is solved through a faster and closed form solution that enables it to work in large-scale settings. We conduct a rigorous statistical analysis showing that surprisingly DIFFEE achieves the same asymptotic convergence rates as the state-of-the-art estimators that are much more difficult to compute. Our experimental results on multiple synthetic datasets and one real-world data about brain connectivity show strong performance improvements over baselines, as well as significant computational benefits.
A Fast and Scalable Joint Estimator for Learning Multiple Related Sparse Gaussian Graphical Models
Mar 20, 2018
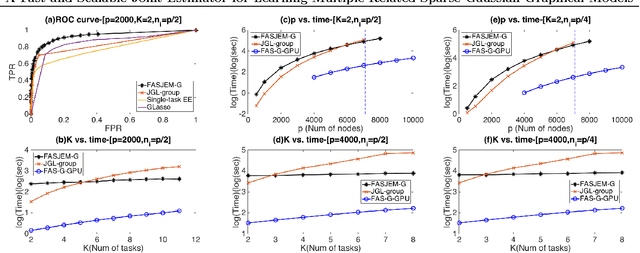

Abstract:Estimating multiple sparse Gaussian Graphical Models (sGGMs) jointly for many related tasks (large $K$) under a high-dimensional (large $p$) situation is an important task. Most previous studies for the joint estimation of multiple sGGMs rely on penalized log-likelihood estimators that involve expensive and difficult non-smooth optimizations. We propose a novel approach, FASJEM for \underline{fa}st and \underline{s}calable \underline{j}oint structure-\underline{e}stimation of \underline{m}ultiple sGGMs at a large scale. As the first study of joint sGGM using the Elementary Estimator framework, our work has three major contributions: (1) We solve FASJEM through an entry-wise manner which is parallelizable. (2) We choose a proximal algorithm to optimize FASJEM. This improves the computational efficiency from $O(Kp^3)$ to $O(Kp^2)$ and reduces the memory requirement from $O(Kp^2)$ to $O(K)$. (3) We theoretically prove that FASJEM achieves a consistent estimation with a convergence rate of $O(\log(Kp)/n_{tot})$. On several synthetic and four real-world datasets, FASJEM shows significant improvements over baselines on accuracy, computational complexity, and memory costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge