Differential Network Learning Beyond Data Samples
Paper and Code
Apr 24, 2020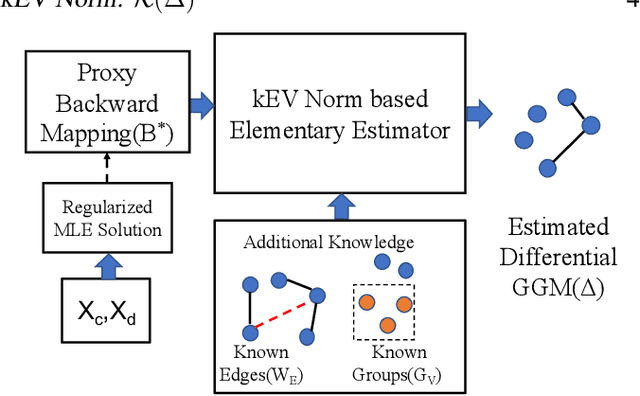
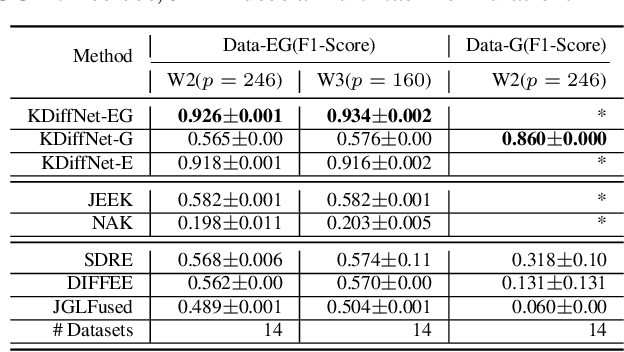
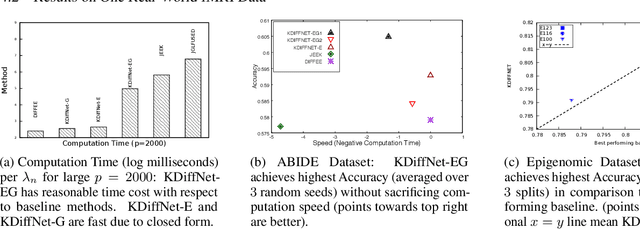
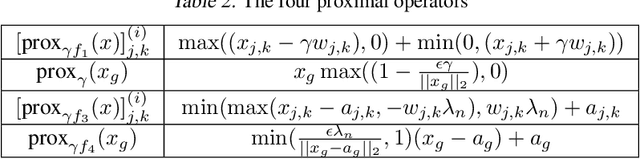
Learning the change of statistical dependencies between random variables is an essential task for many real-life applications, mostly in the high dimensional low sample regime. In this paper, we propose a novel differential parameter estimator that, in comparison to current methods, simultaneously allows (a) the flexible integration of multiple sources of information (data samples, variable groupings, extra pairwise evidence, etc.), (b) being scalable to a large number of variables, and (c) achieving a sharp asymptotic convergence rate. Our experiments, on more than 100 simulated and two real-world datasets, validate the flexibility of our approach and highlight the benefits of integrating spatial and anatomic information for brain connectome change discovery and epigenetic network identification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge