Manta: Enhancing Mamba for Few-Shot Action Recognition of Long Sub-Sequence

In few-shot action recognition~(FSAR), long sub-sequences of video naturally express entire actions more effectively. However, the computational complexity of mainstream Transformer-based methods limits their application. Recent Mamba demonstrates efficiency in modeling long sequences, but directly applying Mamba to FSAR overlooks the importance of local feature modeling and alignment. Moreover, long sub-sequences within the same class accumulate intra-class variance, which adversely impacts FSAR performance. To solve these challenges, we propose a \underline{\textbf{M}}atryoshka M\underline{\textbf{A}}mba and Co\underline{\textbf{N}}tras\underline{\textbf{T}}ive Le\underline{\textbf{A}}rning framework~(\textbf{Manta}). Firstly, the Matryoshka Mamba introduces multiple Inner Modules to enhance local feature representation, rather than directly modeling global features. An Outer Module captures dependencies of timeline between these local features for implicit temporal alignment. Secondly, a hybrid contrastive learning paradigm, combining both supervised and unsupervised methods, is designed to mitigate the negative effects of intra-class variance accumulation. The Matryoshka Mamba and the hybrid contrastive learning paradigm operate in parallel branches within Manta, enhancing Mamba for FSAR of long sub-sequence. Manta achieves new state-of-the-art performance on prominent benchmarks, including SSv2, Kinetics, UCF101, and HMDB51. Extensive empirical studies prove that Manta significantly improves FSAR of long sub-sequence from multiple perspectives. The code is released at https://github.com/wenbohuang1002/Manta.

Label Information Enhanced Fraud Detection against Low Homophily in Graphs

Node classification is a substantial problem in graph-based fraud detection. Many existing works adopt Graph Neural Networks (GNNs) to enhance fraud detectors. While promising, currently most GNN-based fraud detectors fail to generalize to the low homophily setting. Besides, label utilization has been proved to be significant factor for node classification problem. But we find they are less effective in fraud detection tasks due to the low homophily in graphs. In this work, we propose GAGA, a novel Group AGgregation enhanced TrAnsformer, to tackle the above challenges. Specifically, the group aggregation provides a portable method to cope with the low homophily issue. Such an aggregation explicitly integrates the label information to generate distinguishable neighborhood information. Along with group aggregation, an attempt towards end-to-end trainable group encoding is proposed which augments the original feature space with the class labels. Meanwhile, we devise two additional learnable encodings to recognize the structural and relational context. Then, we combine the group aggregation and the learnable encodings into a Transformer encoder to capture the semantic information. Experimental results clearly show that GAGA outperforms other competitive graph-based fraud detectors by up to 24.39% on two trending public datasets and a real-world industrial dataset from Anonymous. Even more, the group aggregation is demonstrated to outperform other label utilization methods (e.g., C&S, BoT/UniMP) in the low homophily setting.

Contextual-Bandit Based Personalized Recommendation with Time-Varying User Interests

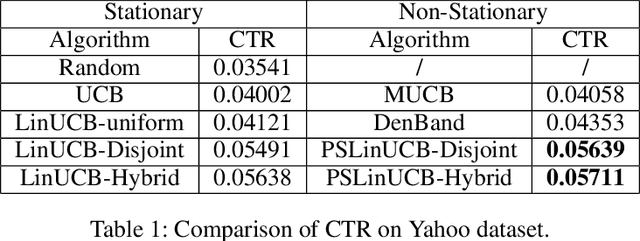
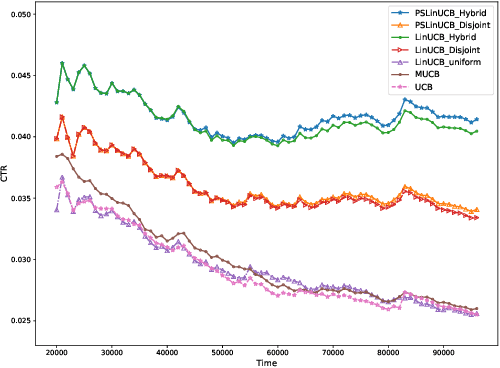
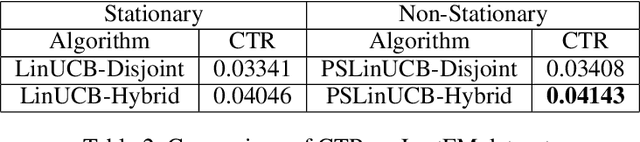
A contextual bandit problem is studied in a highly non-stationary environment, which is ubiquitous in various recommender systems due to the time-varying interests of users. Two models with disjoint and hybrid payoffs are considered to characterize the phenomenon that users' preferences towards different items vary differently over time. In the disjoint payoff model, the reward of playing an arm is determined by an arm-specific preference vector, which is piecewise-stationary with asynchronous and distinct changes across different arms. An efficient learning algorithm that is adaptive to abrupt reward changes is proposed and theoretical regret analysis is provided to show that a sublinear scaling of regret in the time length $T$ is achieved. The algorithm is further extended to a more general setting with hybrid payoffs where the reward of playing an arm is determined by both an arm-specific preference vector and a joint coefficient vector shared by all arms. Empirical experiments are conducted on real-world datasets to verify the advantages of the proposed learning algorithms against baseline ones in both settings.