Contextual-Bandit Based Personalized Recommendation with Time-Varying User Interests
Paper and Code
Feb 29, 2020
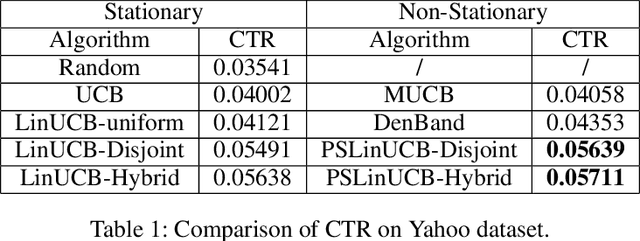
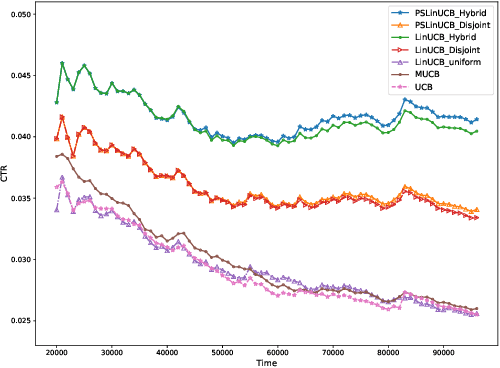
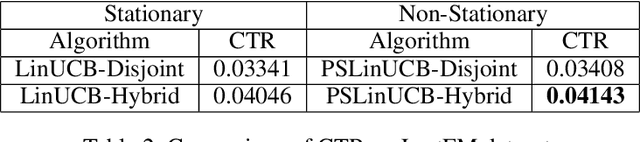
A contextual bandit problem is studied in a highly non-stationary environment, which is ubiquitous in various recommender systems due to the time-varying interests of users. Two models with disjoint and hybrid payoffs are considered to characterize the phenomenon that users' preferences towards different items vary differently over time. In the disjoint payoff model, the reward of playing an arm is determined by an arm-specific preference vector, which is piecewise-stationary with asynchronous and distinct changes across different arms. An efficient learning algorithm that is adaptive to abrupt reward changes is proposed and theoretical regret analysis is provided to show that a sublinear scaling of regret in the time length $T$ is achieved. The algorithm is further extended to a more general setting with hybrid payoffs where the reward of playing an arm is determined by both an arm-specific preference vector and a joint coefficient vector shared by all arms. Empirical experiments are conducted on real-world datasets to verify the advantages of the proposed learning algorithms against baseline ones in both settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge